11.5: CONEXIONES NO LINEALES
- Page ID
- 84327
Las topologías presentadas en la Sección 11.4 estaban destinadas a proporcionar ganancias lineales, funciones de transferencia o impedancias. Si bien las realizaciones prácticas de estos circuitos pueden incluir elementos no lineales, la retroalimentación está dispuesta para minimizar los efectos de tales no linealidades. En muchos otros casos, la retroalimentación implementada por medio de amplificadores operacionales se usa para aumentar, controlar o idealizar las características de los elementos no lineales. En esta sección se presentan ejemplos de este tipo de aplicaciones.
Rectificadores de precisión
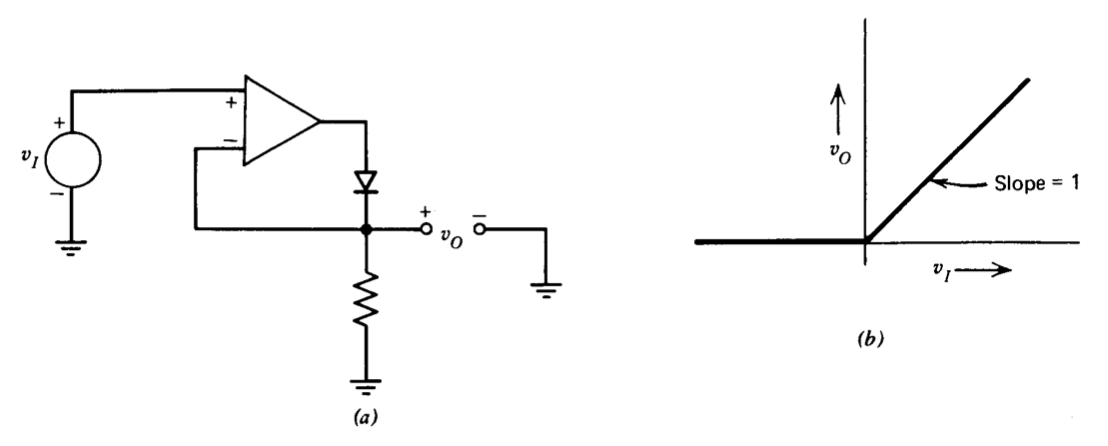
Muchas conexiones de circuito utilizan diodos para rectificar señales. Sin embargo, la caída de tensión directa asociada con un diodo limita su capacidad para rectificar señales de bajo nivel. La combinación de un diodo con un amplificador operacional (Figura 11.18) da como resultado un circuito con un umbral mucho más bajo. El funcionamiento depende del hecho de que la combinación de diodo-amplificador solo puede extraer el voltaje de salida positivo, de modo que los voltajes de entrada negativos dan como resultado una salida cero. Con un voltaje de entrada positivo, se amplifica una señal diferencial insignificante pequeña (igual al voltaje umbral del diodo dividido por la ganancia de bucle abierto del amplificador) para proporcionar suficiente voltaje de salida del amplificador para superar el umbral del diodo, con el resultado de que
\[v_O = v_I \ \ \ \ v_I > 0 \nonumber \]
\[v_O = 0 \ \ \ \ v_I < 0 \nonumber \]
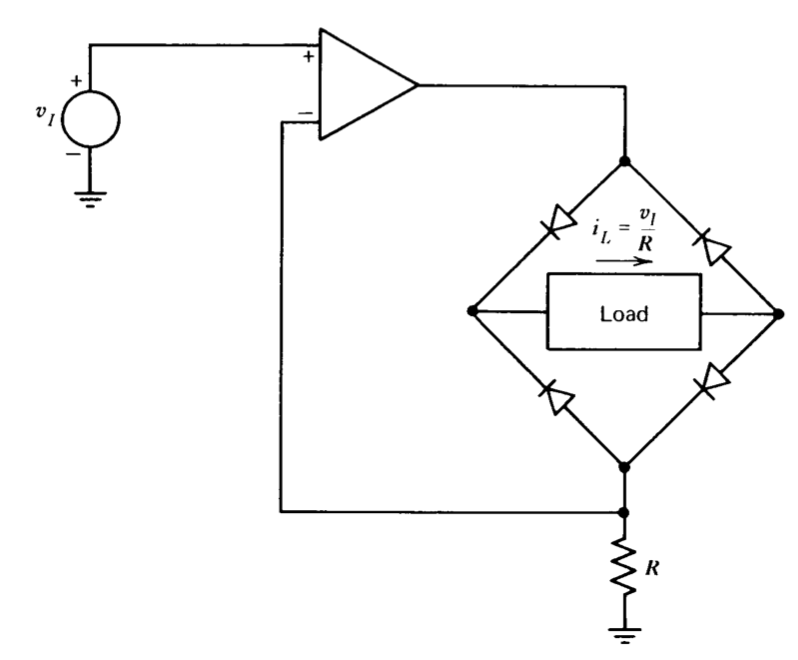
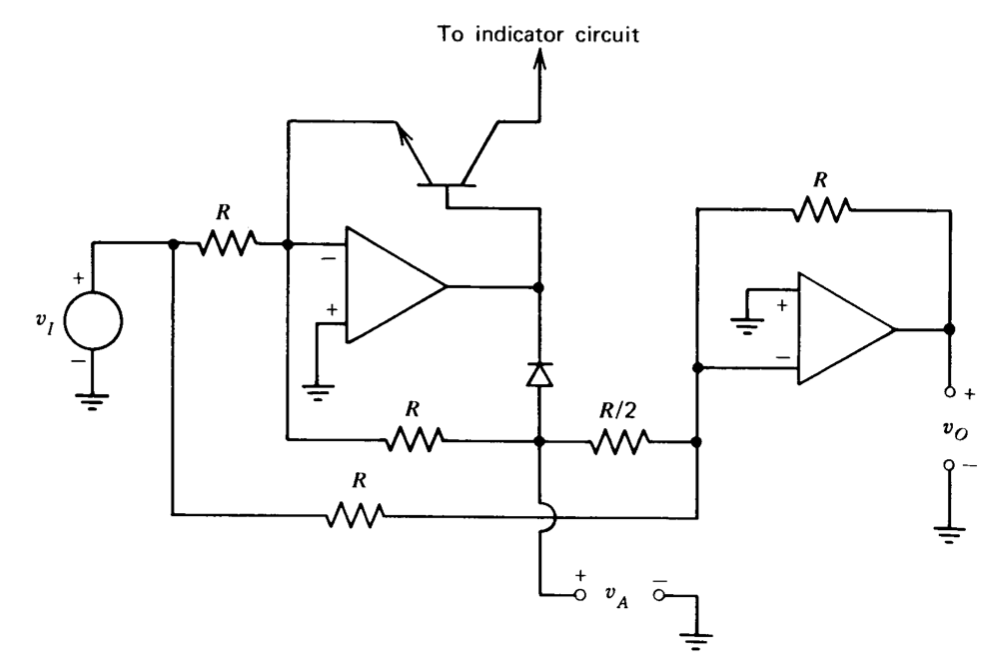
Existen muchas variaciones de este rectificador de precisión o “superdiodo”. Por ejemplo, el circuito mostrado en la Figura 11.19 rectifica y proporciona un accionamiento de fuente de corriente para una carga flotante tal como un movimiento de medidor D'Arsonval. La Figura 11.20 ilustra otro circuito rectificador. Con\(v_I\) negativo, el voltaje\(v_A\) es cero, y\(v_O = - v_I\) debido a la inversión proporcionada por el amplificador de mano derecha. El transistor proporciona una ruta de realimentación para el primer amplificador de manera que permanece en su región lineal para entradas negativas. La operación en la región lineal mantiene la entrada inversora del primer amplificador a potencial de tierra, evitando así que la señal de entrada conduzca el voltaje\(v_A\) a través de alimentación resistiva directa. El mantenimiento de la operación de región lineal también elimina los largos tiempos de recuperación del amplificador que frecuentemente acompañan a la sobrecarga y saturación. Si bien se podría usar un diodo en lugar del transistor, el transistor proporciona un método conveniente para activar más cuits cir amplificadores, que indican la polaridad de la señal de entrada si se requiere esta función. Para voltajes de entrada positivos, voltaje\(v_A = - v_I\), para que la resistencia con valor\(R/2\) también aplique corriente a la entrada del segundo amplificador, con el resultado de que
\[v_O = -(v_I - 2v_I) = v_I \ \ \ \ v_I > 0 \nonumber \]
\[v_O = -v_I \ \ \ \ \ \ \ \ \ \ \ v_I < 0 \nonumber \]
Detector de Pico
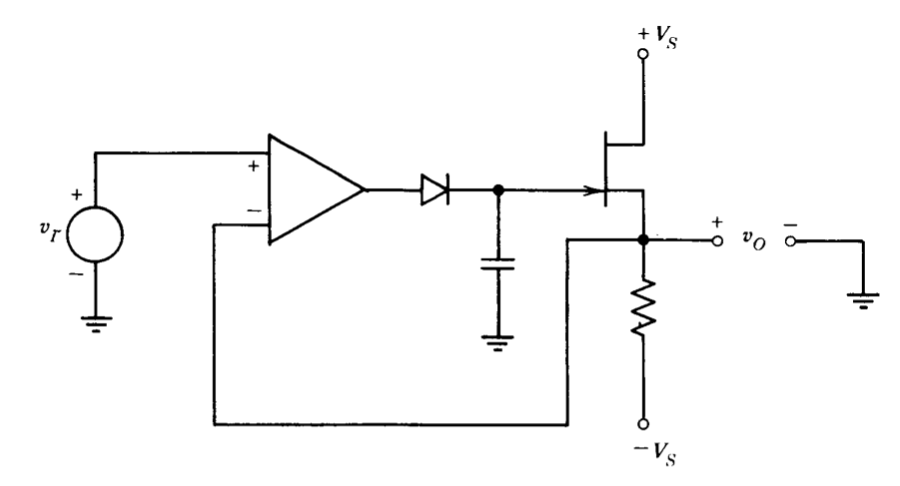
El circuito detector de picos que se muestra en la Figura 11.21 ilustra una elaboración adicional sobre el tema general de minimizar los efectos de las caídas de voltaje en varios elementos al incluir estas caídas dentro de un bucle de retroalimentación. Si el voltaje de salida es más positivo que el voltaje de entrada, la salida del amplificador operacional se saturará en la dirección negativa. (Se puede incluir alguna forma de sujeción para acelerar la recuperación de este estado). En estas condiciones, la corriente del condensador consiste únicamente en corrientes de fuga de diodo y puerta FET; por lo tanto, el voltaje del condensador cambia muy lentamente. Como cuestión de preocupación práctica, el circuito funcionará correctamente solo si los niveles de corriente son tales que el voltaje del condensador deriva negativamente en este estado. De lo contrario, la conexión eventualmente se saturará en su nivel de salida positivo máximo.
Si\(v_I\) se vuelve mayor que\(v_O\), el condensador se carga rápidamente desde la salida del amplificador operacional a través del diodo hasta que se restafirme la igualdad. Tenga en cuenta que el voltaje del condensador no está obligado a ser igual a\(v_I\), sino más bien a ser igual a un voltaje que, combinado con el voltaje de puerta a fuente de FET, fuerza la igualdad entre\(v_O\) y\(v_I\). De esta manera la tensión de salida “recuerda” el valor más positivo de la señal de entrada.
Generación de características de transferencia lineal por pieza
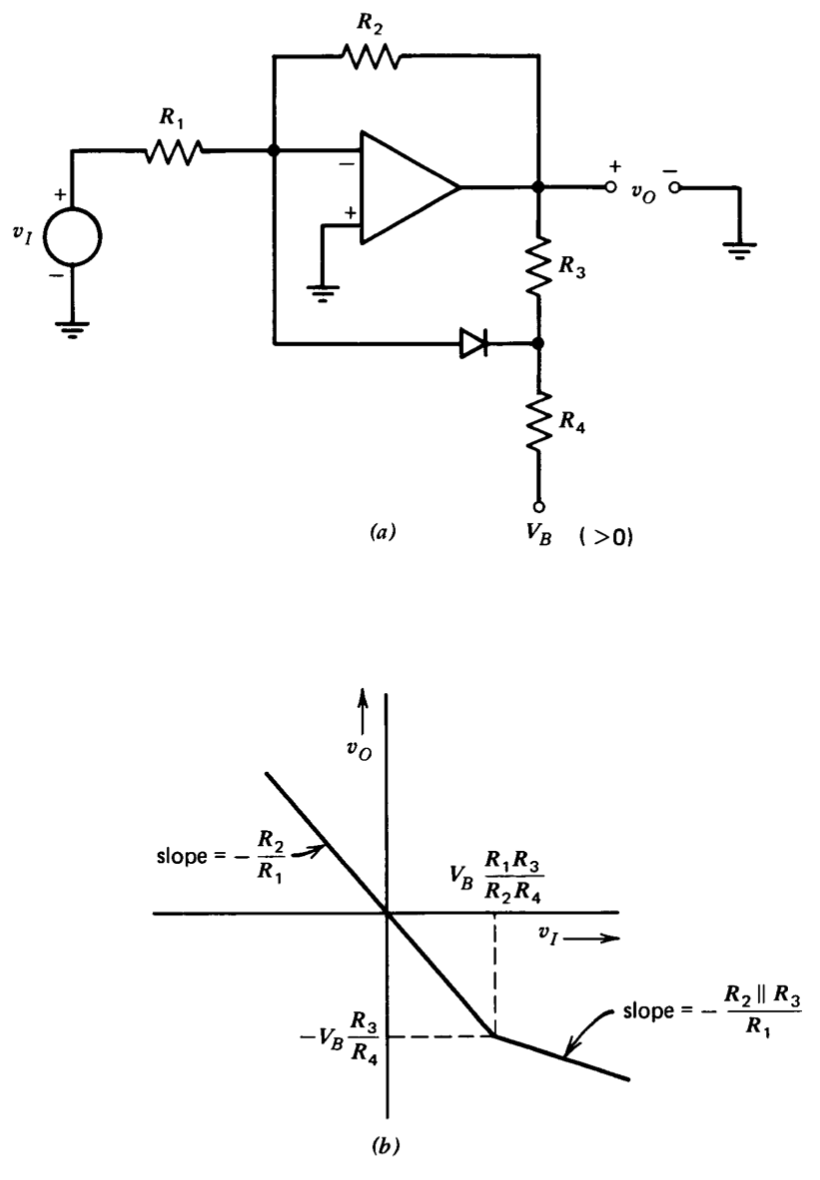
Los diodos se pueden combinar con amplificadores operacionales para realizar circuitos de conformación de señal que no sean rectificadores. La Figura 11.22 muestra un circuito que proporciona una relación de transferencia no lineal de tipo compresivo o limitante. Para voltajes de entrada más negativos que\(V_B (R_1R_3/R_2 R_4)\) el diodo es un circuito abierto, y la ganancia incremental del circuito es\(-R_2/R_1\). Cuando\(v_I = V_B(R_1R_3/R_2 R_4)\), el diodo está en el umbral de conducción. Suponiendo un diodo “perfecto” (voltaje de umbral cero y cero en la resistencia en la dirección hacia adelante), la resistencia de retroalimentación efectiva para mayores aumentos en el voltaje de entrada es\(R_2 || R_3\), y la magnitud de la ganancia incremental disminuye a\(-(R_2 || R_3)/R_1\).
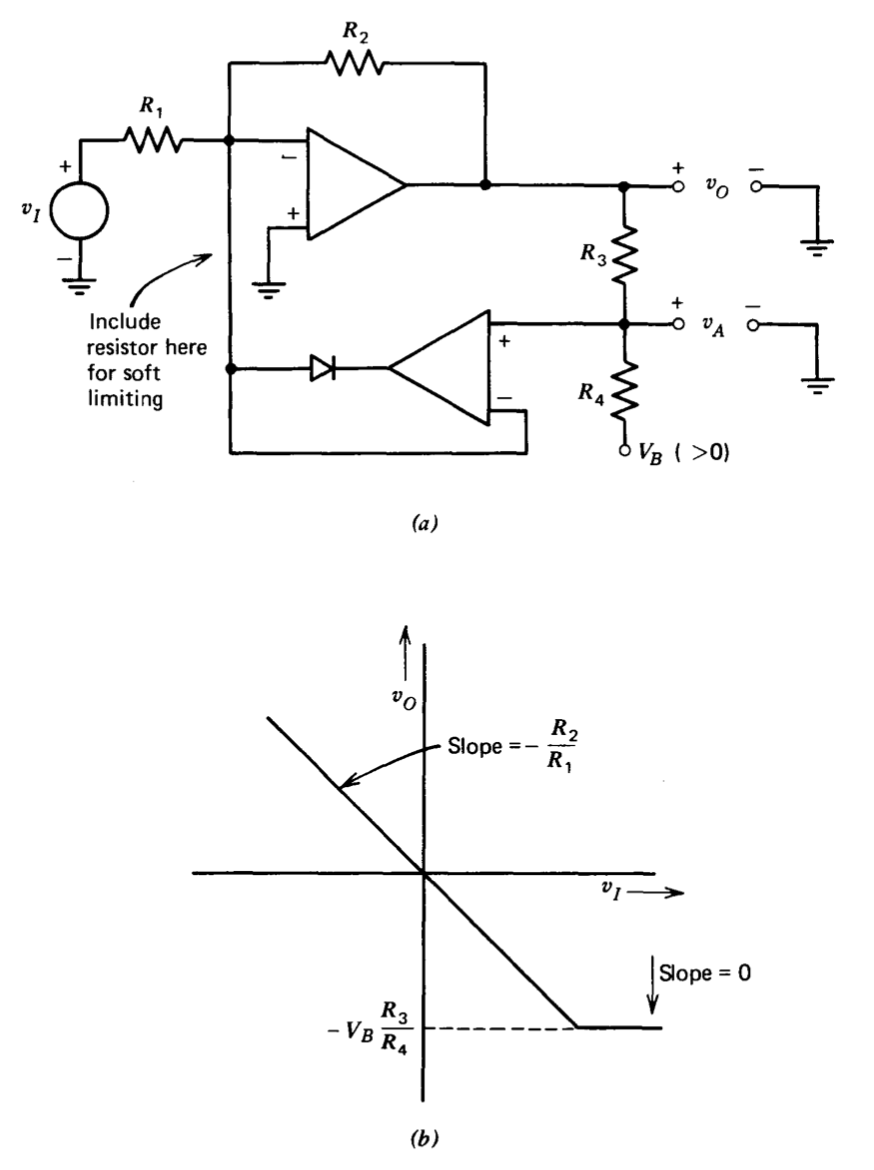
Se describió el funcionamiento del limitador asumiendo características de carbonización de diodo perfectas. Si la degradación del rendimiento que resulta de las características reales del diodo es intolerable, se puede usar una conexión de “superdiodo” como se muestra en la Figura 11.23. El amplificador operacional inferior no puede afectar el funcionamiento del circuito para los valores positivos de VA que corresponden a voltajes de entrada más negativos que\(V_B (R_1R_3/R_2R_4)\) porque el diodo en serie con su salida es polarizado inverso. Sin embargo, el amplificador inferior puede suministrar tanta corriente como se requiera para mantener el voltaje en la unión\(R_4\) de\(R_3\) y no volverse negativo, y por lo tanto este circuito proporciona una limitación dura con la ganancia incremental cayendo a cero para voltajes de entrada más positivos que el nivel umbral. Si se requiere una limitación más suave, se puede incluir una resistencia en el punto indicado.
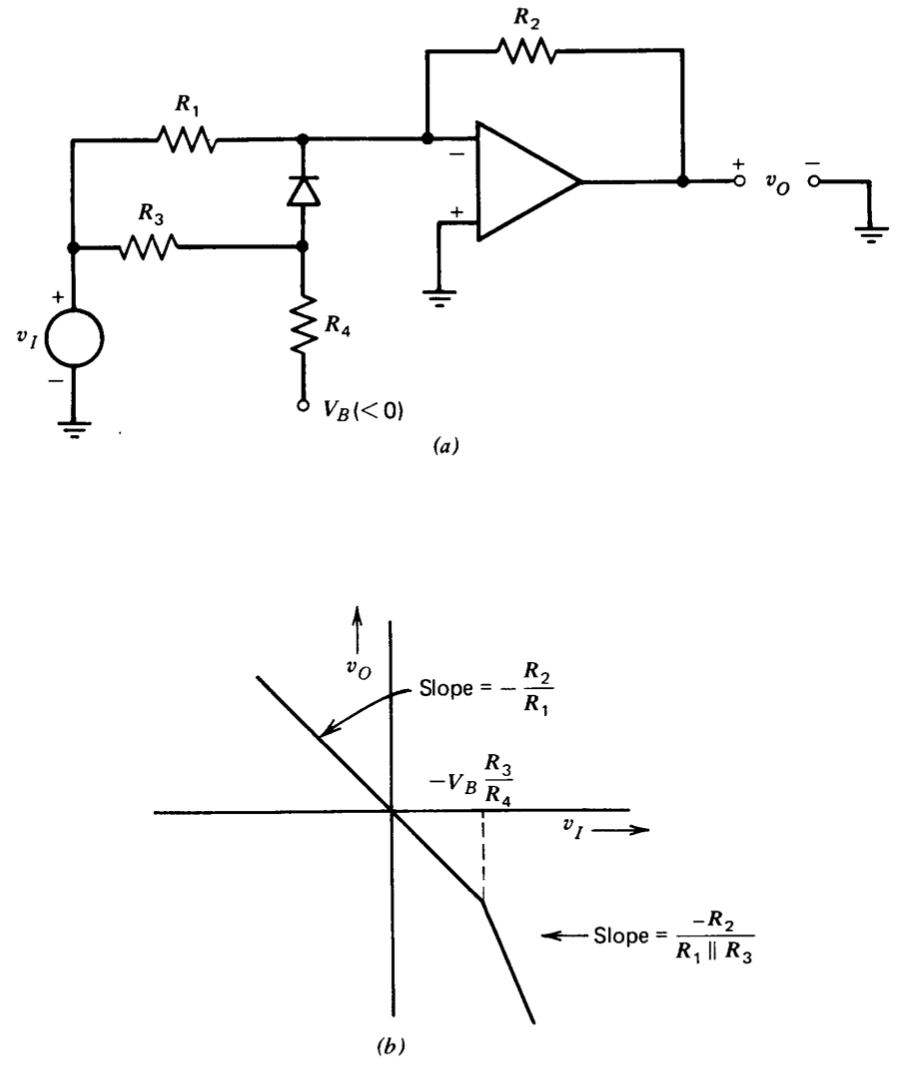
Está claro que se pueden agregar redes de resistencias adicionales y diodos (o superdiodos) para aumentar el número de puntos de ruptura en las características de transferencia. Sin embargo, la topología de la Figura 11.22 o la Figura 11.23 impide aumentar la magnitud de la ganancia incremental a medida que aumenta la magnitud del voltaje de entrada. Desplazar la red diodo-resistor al circuito de entrada del amplificador (Figura 11.24) es una forma en que se pueden realizar no linealidades de tipo expansivo.
Circuitos Antilog
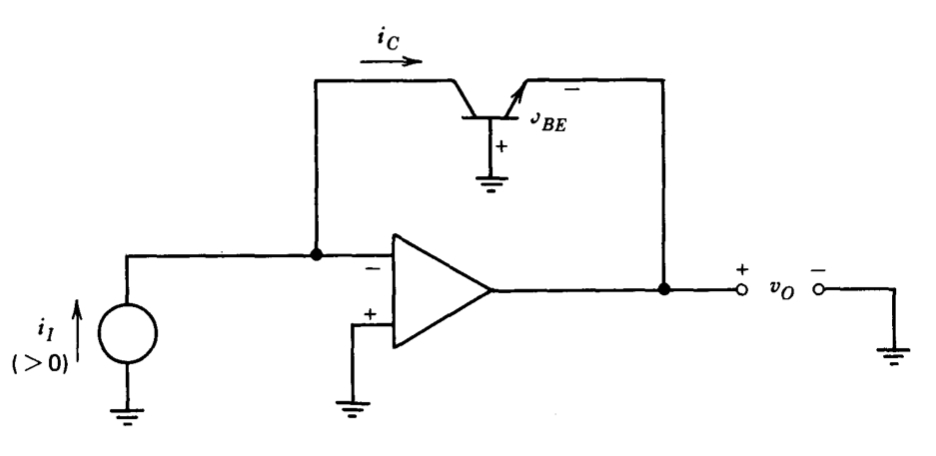
Las características exponenciales de corriente-voltaje de diodos o transistores pueden explotarse para realizar circuitos con características exponenciales o logarítmicas. La Figura 11.25 ilustra un circuito muy simple que proporciona una relación logarítmica entre el voltaje de salida y la corriente de entrada. En condiciones normales de funcionamiento, el amplificador operacional mantiene el voltaje colector a base del transistor en cero. Como resultado, se eliminan las corrientes de fuga de unión de colector a base al igual que los efectos de modulación de ancho de base, y muchos tipos de transistores seguirán con precisión la relación
\[i_C \simeq I_S e^{qv_{BE}/kT} \label{eq11.5.5} \]
en un rango de niveles de corriente de operación que se extiende desde picoamperios hasta una fracción de miliamperios. La desviación del comportamiento puramente exponencial ocurre a niveles de corriente comparables a\(I_S\) y a niveles de corriente donde las resistencias óhmicas se vuelven significativas. (Teóricamente, un diodo podría ser utilizado como un elemento de retroalimentación como se indica en la Sección 1.2.3 para obtener características logarítmicas de bucle cerrado. En la práctica, la conexión de transistor ilustrada aquí es preferible, ya que los transistores generalmente muestran las características deseadas en un rango dinámico mucho mayor que los diodos).
Para esta topología de circuito,\(V_{BE} = - v_O\), y la retroalimentación mantiene\(i_C = i_I\). Sustituir estas restricciones en Ecuación\(\ref{eq11.5.5}\) muestra que
\[i_I = I_S e^{-q v_O/kT} \nonumber \]
o, si resolvemos para\(v_O\),
\[v_O = -\dfrac{kT}{q} \ln \dfrac{i_I}{I_S} \nonumber \]
Por supuesto, la corriente aplicada a este circuito se puede derivar de una tensión de entrada disponible a través de una resistencia conectada al terminal de entrada inversora del amplificador operacional. En este caso, el desplazamiento de voltaje del amplificador operacional aporta un término de error que normalmente limita el rango dinámico a tres o cuatro órdenes de magnitud. Si la señal de entrada está disponible como corriente, como lo es para algunos sensores como los medidores de ionización, es posible un rango dinámico mucho más amplio para una corriente de polarización del amplificador suficientemente baja.
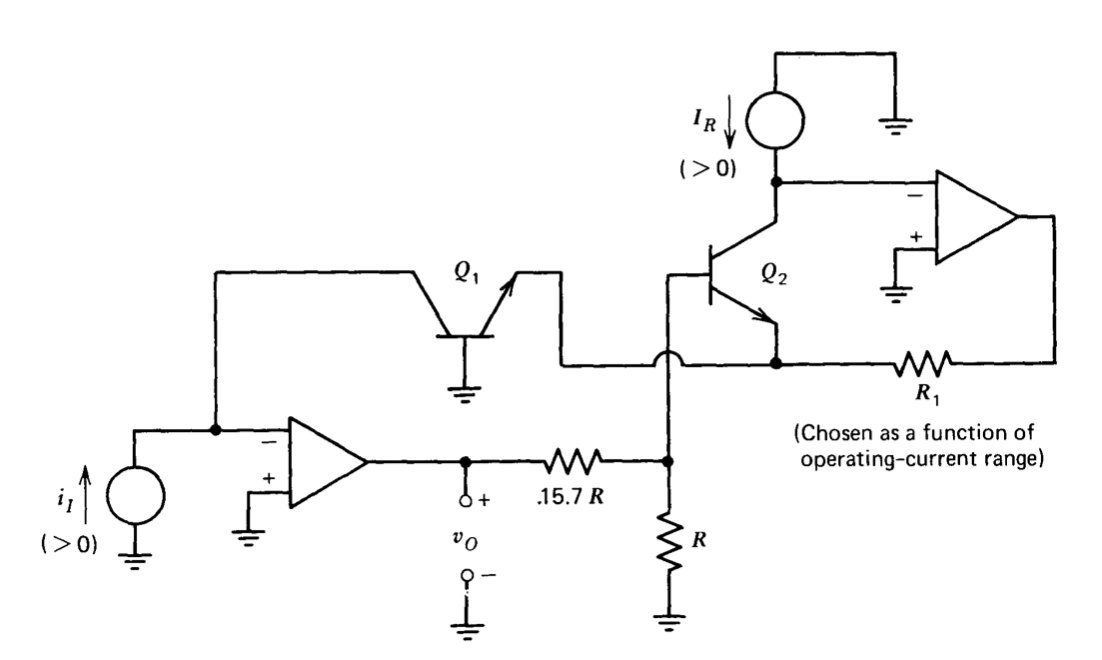
Una deficiencia de este circuito simple es que la cantidad\(I_S\) es altamente dependiente de la temperatura (ver Sección 7.2). El circuito que se muestra en la Figura 11.26 ofrece un rendimiento mejorado con la temperatura. La retroalimentación a través del amplificador operacional derecho mantiene la corriente del colector\(Q_2\) igual a la corriente de referencia\(I_R\); así
\[v_{BE2} = \dfrac{kT}{q} \ln \dfrac{I_R}{I_{S2}} \label{eq11.5.8} \]
Tenga en cuenta que, dado que el potencial en el colector de\(Q_2\) se mantiene a cero voltios por el amplificador operacional, la corriente de referencia se obtiene fácilmente a través de una resistencia conectada a una tensión de alimentación positiva.
El amplificador operacional izquierdo ajusta el voltaje base de\(Q_2\), cambiando así el voltaje de base a emisor de\(Q_1\) hasta que la corriente del colector\(Q_1\) sea igual\(i_I\), con el resultado de que
\[v_{BE1} = \dfrac{kT}{q} \ln \dfrac{i_I}{I_{S1}} \nonumber \]
Si se seleccionan valores para que la corriente base de\(Q_2\) no cargue el atenuador de circuito base, la relación de voltaje es
\[v_{BE1} = v_{BE2} - \dfrac{1}{16.7} v_O \label{eq11.5.10} \]
\(\ref{eq11.5.8}\)Combinando ecuaciones\(\ref{eq11.5.10}\) y resolviendo\(v_O\) rendimientos
\[v_O = -16.7 \dfrac{kT}{q} \left [ \ln \dfrac{i_I}{I_{S1}} - \ln \dfrac{I_R}{I_{S2}} \right ] = -16.7 \dfrac{kT}{q} \ln \left [ \dfrac{i_I}{i_R} \dfrac{I_{S2}}{I_{S1}} \right ] \label{eq11.5.11} \]
Si los transistores\(Q_1\) y\(Q_2\) tienen valores bien emparejados de\(I_S\), la ecuación\(\ref{eq11.5.11}\) se convierte
\[v_O = -16.7 \dfrac{kT}{q} \ln \left [\dfrac{i_I}{i_R} \right ] \label{eq11.5.12} \]
Se utiliza la relación de atenuación resistivo-divisor de 16.7 para que a temperatura ambiente, la ecuación se\(\ref{eq11.5.12}\) reduzca a
\[v_O = -1 \text{ volt }\log_{10} \left [\dfrac{i_I}{i_R} \right ] \nonumber \]
Si bien el uso de transistores emparejados como se muestra en la Figura 11.26 elimina la dependencia de la salida en\(I_S\), la Ecuación\(\ref{eq11.5.12}\) muestra que el factor de escala del circuito es proporcional a la temperatura absoluta. Una solución común es compensar usando una resistencia con un valor inversamente proporcional a la temperatura absoluta como la menor de las dos resistencias en el divisor de voltaje.
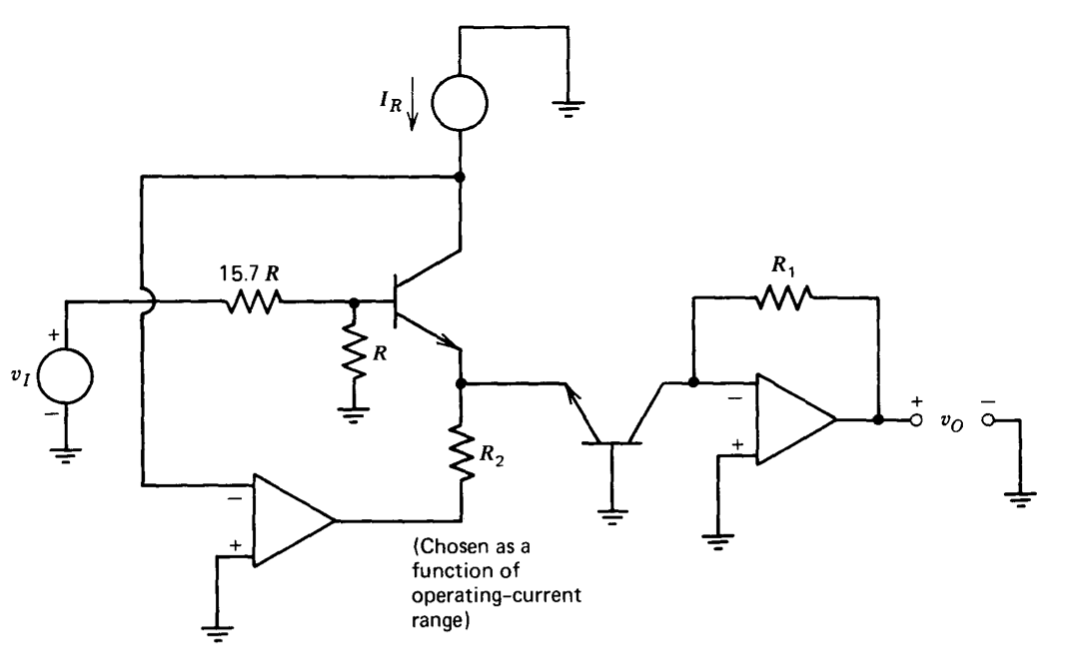
El circuito antilogarítmico mostrado en la Figura 11.27 resulta de la reorganización de componentes. El lector debe verificar que, a temperatura ambiente y con transistores emparejados, la relación entrada-salida para este circuito es
\[v_O = R_1 I_R \times 10^{-(v_I/\text{1 volt})} \nonumber \]
Multiplicación analógica
Hay una serie de configuraciones que realizan multiplicación analógica, es decir, proporcionan un voltaje de salida proporcional al producto de dos voltajes de entrada. Por ejemplo, uno o más circuitos logarítmicos se pueden combinar con un circuito antilogarítmico para realizar multiplicadores, divisores o circuitos que elevan un voltaje a una potencia. Otra técnica conocida como multiplicación de cuarto de cuadrado explota la relación
\[(v_X + v_Y)^2 - (v_X - v_Y)^2 = 4 v_X v_Y \nonumber \]
Las características de transferencia cuadrática se pueden aproximar con conexiones de amplificador operacional de diodos lineales por tramos.
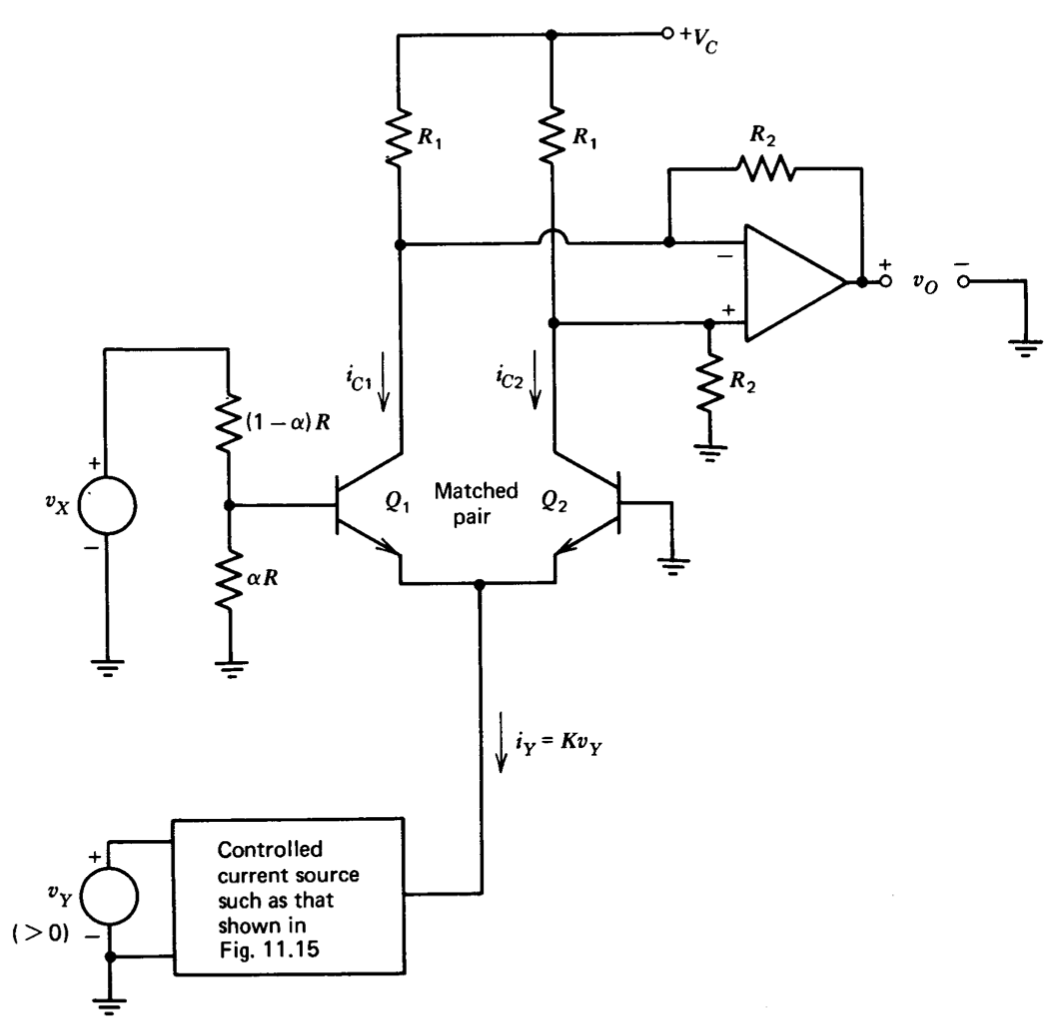
Un método conocido como multiplicación de transconductancia es la base de varios multiplicadores analógicos discretos y de circuito integrado disponibles porque es capaz de una precisión moderada y requiere relativamente pocos componentes. En la Figura 11.28 se muestra un multiplicador de transconductancia simplificado (limitado a la operación de dos cuadrantes porque el voltaje\(v_Y\) no puede ser negativo).
Si se supone que el\(v_X\) atenuador no está cargado por la corriente de entrada del transistor\(Q_1\) y que el voltaje de entrada diferencial aplicado al par es lo suficientemente pequeño como para que las relaciones de región lineal sean válidas para los transistores, la diferencia entre las dos corrientes de colector es
\[i_{C1} - i_{C2} = \alpha v_X g_m \label{eq11.5.16} \]
donde\(g_m\) es la transconductancia (igual) de cualquiera de los dos transistores.
Para la operación de señal pequeña, la cantidad\(g_m\) está relacionada con la corriente de funcionamiento en reposo, la cual a su vez está determinada por la variable de entrada\(v_Y\). Por lo tanto,
\[g_m = \dfrac{i_Y q}{2kT} = \dfrac{Kv_Y q}{2kT} \label{eq11.5.17} \]
Sustituir la ecuación\(\ref{eq11.5.17}\) en ecuación\(\ref{eq11.5.16}\) muestra que
\[i_{C1} - i_{C2} = \dfrac{\alpha Kq}{2kT} v_X v_Y \label{eq11.5.18} \]
El lector debe convencerse a sí mismo de que el amplificador operacional conectado diferencialmente proporciona un voltaje de salida igual a\(R_2\) veces la diferencia entre las dos corrientes del colector. Sustituir esta relación en Ecuación\(\ref{eq11.5.18}\) rinde
\[v_O = \dfrac{\alpha KR_2q}{2kT} v_X v_Y \label{eq11.5.19} \]
Hay una serie de limitaciones de diseño necesarias para una operación satisfactoria o introducidas por conveniencia, incluyendo las siguientes.
(a) La corriente normalmente\(i_Y\) se limita a una fracción de miliamperios para que el rendimiento no se degrada por la resistencia del transistor óhmico.
(b) La relación de atenuación a debe elegirse para limitar el voltaje de entrada aplicado al par de transistores a un nivel bajo. Los cálculos detallados muestran que la inexactitud atribuible a las características exponenciales del transistor puede limitarse a menos del 1% de la salida máxima si la magnitud máxima de la tensión en el par diferencial se mantiene por debajo de aproximadamente\(8\ mV\).
(c) Debido a los limitados niveles de señal aplicados al par diferencial, su deriva tiene un efecto significativo en el desempeño general. El circuito se puede equilibrar ajustando la relación de las dos resistencias etiquetadas\(R_1\) en la Figura 11.28.
(d) La dependencia de la temperatura de la Ecuación\(\ref{eq11.5.19}\) puede compensarse haciendo que la relación voltaje-atenuador o la temperatura del factor de escala corriente-fuente dependan de la temperatura.
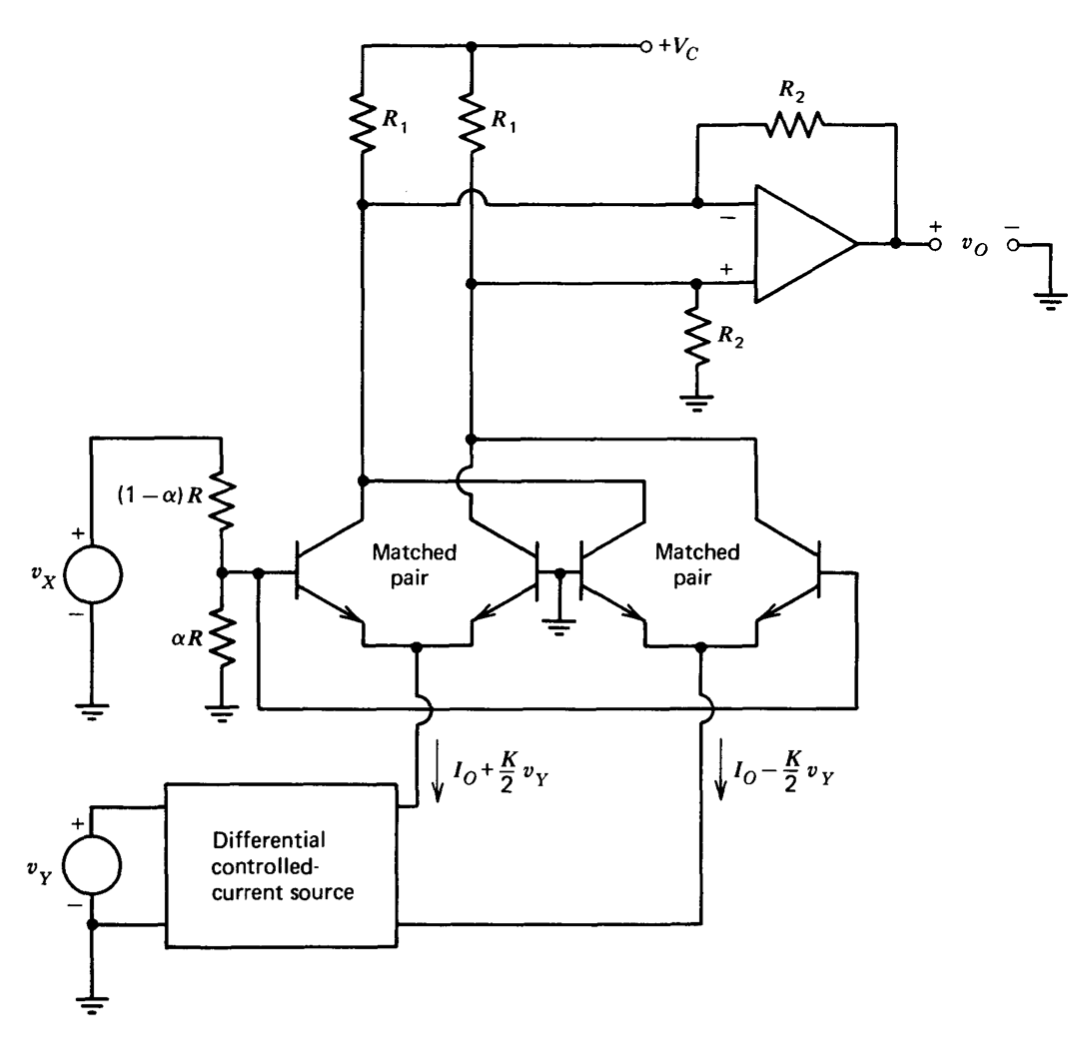
(e) La restricción de valores de polaridad única para la\(v_Y\) entrada se puede eliminar mediante la inclusión de un segundo par diferencial de transistores, y haciendo que las corrientes de funcionamiento de los dos pares varíen diferencialmente en función de\(v_Y\). Se invita al lector interesado a mostrar que la relación entrada-salida para el multiplicador de transconductancia de cuatro cuadrantes que se muestra en la Figura 11.29 viene dada por la Ecuación\(\ref{eq11.5.19}\).
(f) El factor de escala se ajusta frecuentemente para dar\(v_O = v_Xv_Y/10\) voltios, un valor compatible con los niveles de señal comunes a muchos sistemas analógicos.
En general, lograr un desempeño altamente preciso a partir de un multiplicador de transconductancia implica una serie bastante compleja de ajustes para nular diversas fuentes de error. Este proceso se simplifica un poco por una innovación desarrollada por Gilbert (. Gilbert, “A D.C.-500 MHz Amplifier/Multiplifier Principle”, Digest of Technical Papers, 1968 Solid-State Circuits Conference, Philadelphia, Pa.) que utiliza diodos compensadores para eliminar la dependencia de la temperatura del factor de escala y aumentar los niveles de señal que pueden aplicarse a los pares diferenciales. Si bien hay problemas que deben superarse, la técnica es lo suficientemente buena para que varios fabricantes ofrezcan multiplicadores de transconductancia económicos con errores de todas las fuentes de menos del 1% de la salida máxima.


