5.10: Problemas
- Page ID
- 87929
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)5.10.1: Preguntas de revisión
1. Definir producto de ganancia de ancho de banda. ¿Cuál es su uso?
2. ¿Cómo se determina\(f_2\) y\(f_1\) para un circuito multietapa?
3. ¿Qué sucede si dos o más etapas comparten la misma frecuencia de ruptura?
4. ¿Qué es la tasa de giro?
5. ¿Cómo se determina el ancho de banda eléctrico?
6. ¿En qué se diferencian el ancho de banda de potencia y el ancho
7. ¿Cuáles son las ventajas y desventajas de los amplificadores operacionales no compensados?
8. ¿Qué son los amplificadores operacionales descompensados?
9. ¿Qué causa el voltaje de compensación de CC?
10. ¿Qué causa el voltaje de deriva de CC?
11. ¿Qué es CMRR?
12. ¿Qué es PSRR?
13. ¿Qué parámetros describen un rendimiento de ruido de amplificadores operacionales?
14. ¿Qué es S/N?
5.10.2: Problemas
Problemas de análisis
1. Determine\(f_2\) para el circuito en la Figura 5.3.3 si se utiliza un amplificador operacional 411.
2. Determine\(f_2\) para el circuito de la Figura 5.3.5 si se usa un amplificador operacional 318. Nota:\(f_{unity}\) = 15 MHz para un 318.
3. ¿Cuál es el mínimo aceptable\(f_{unity}\) para el amplificador operacional en la Figura 5.3.3 si el deseado\(f_2\) es de 250 kHz?
4. ¿Cuál es el mínimo aceptable\(f_{unity}\) para el amplificador operacional en la Figura 5.3.5 si el deseado\(f_2\) es de 20 kHz?
5. Determine el ancho de banda de potencia para el Problema 5.1. Supongamos\(V_p\) = 10 V.
6. Determine el ancho de banda de potencia para el Problema 5.3. Supongamos\(V_p\) = 12 V.
7. ¿Cuál es la tasa de respuesta mínima aceptable para el circuito de la Figura 5.3.3 si el ancho de banda de potencia deseado es de 20 kHz con un\(V_p\) de 10 V?
8. ¿Cuál es la tasa de respuesta mínima aceptable para el circuito de la Figura 5.3.5 si el ancho de banda de potencia deseado es de 40 kHz con un\(V_p\) de 5 V?
9. Un circuito tiene las siguientes especificaciones: fuente de alimentación de\(\pm\) 15 V, ganancia de voltaje es igual a 26 dB, ancho de banda de potencia deseado es igual a 80 kHz en el recorte. Determine la tasa de respuesta mínima aceptable para el amplificador operacional.
10. Determine el sistema\(f_2\) en la Figura 5.3.6 si los tres dispositivos son 318s.
11. Determine la tasa de respuesta del sistema para la Figura 5.3.7. El primer dispositivo es un 741 y la segunda unidad es un 411.
12. Encuentre el voltaje de compensación de salida para la Figura 5.3.3.
13. Si\(R_s = R_f = 100 \Omega \) en la Figura 5.5.2, encuentre el voltaje de compensación de salida usando un amplificador de 318 op.
14. Supongamos que el circuito de la Figura 5.5.3 está anulado a 25\(^{\circ}\) C y que\(R_{off}\) se utiliza un valor óptimo para. Determinar la deriva a 75\(^{\circ}\) C.
15. Suponiendo que la ondulación de la fuente de alimentación de 120 Hz en la Figura\(\PageIndex{1}\) es 50 mV, ¿qué tan grande es su contribución a la salida
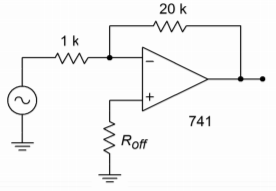
Figura\(\PageIndex{1}\)
16. Utilizando un amplificador operacional 5534, ¿cuál es el voltaje de ruido de entrada aproximado para una resistencia de fuente de 1 k\(\Omega \) y un ancho de banda de 10 Hz a 20 kHz?
17. Suponiendo que el amplificador operacional del Problema 5.16 está conectado como Figura\(\PageIndex{1}\), ¿cuál es el voltaje de ruido de salida aproximado? ¿Cuál es el voltaje aproximado de ruido referido de entrada?
18. Supongamos que\(R_s = 0 \Omega \)\(R_i = 500 \Omega \),, y\(R_f = 10 k\Omega \) en la Figura 5.8.2. Encuentre el voltaje de ruido de entrada si el amplificador operacional es un 411.
19. Para un voltaje de salida nominal de 2 V RMS, determine la relación señal/ruido para Problema 5.18. Supongamos que la entrada a la Figura 5.5.2 es una onda cuadrada de pico de 5 V de 50 kHz. Dibuje la forma de onda de salida si se usa un 741.
21. Repita el problema 5.20 usando una onda sinusoidal de pico de 10 V y 100 kHz.
Problemas de diseño
22. Determinar un valor óptimo para\(R_{off}\) en la Figura 5.3.3 y determinar el voltaje de compensación resultante.
23. Determinar el valor óptimo para\(R_{off}\) en la Figura\(\PageIndex{1}\). Suponiendo que el circuito haya sido anulado a 25\(^{\circ}\) C, encuentre la deriva a 60\(^{\circ}\) C.
24. Determine un nuevo valor para la\(\Omega \) resistencia de 100 k en la Figura 5.3.8 con el fin de minimizar el desplazamiento de salida.
25. Usando la resistencia óptima que se encuentra en el Problema 5.24, determine un nuevo valor para el condensador de entrada que mantendrá el original\(f_1\).
26. Diseñar un circuito con una ganancia de 32 dB y una\(f_2\) de al menos 100 kHz. Puede utilizar cualquiera de los siguientes: 741, 411, 318.
27. Diseñar un circuito con una ganancia de 50 y una\(f_{max}\) de al menos 50 kHz, dada una oscilación de salida máxima de pico de 10 V. Puede utilizar cualquiera de los siguientes: 741, 411, 318.
28. Diseñe un circuito con una ganancia de 12 dB, un ancho de banda de señal pequeña de al menos 100 kHz y un\(f_{max}\) de al menos 100 kHz para una oscilación de salida pico de 12 V.
29. Utilizando dos o más etapas, diseñe un circuito con una ganancia de 150 y un ancho de banda de señal pequeño de al menos 600 kHz.
Problemas de desafío
30. Determinar el sistema\(f_2\) en la Figura 5.4.10.
31. Determine el voltaje de ruido de entrada para el circuito de la Figura\(\PageIndex{1}\). Asumir\(R_{off}\) = 950\(\Omega \).
32. Determine el voltaje de ruido de salida y el voltaje de ruido referido a la entrada para Problema 5.31.
33. Suponiendo que la resistencia de la fuente de accionamiento en la Figura 5.3.7 es 0\(\Omega \), ¿cuánto voltaje de compensación se produce en la salida del circuito? Supongamos que ambos dispositivos son 41's.
34. Supongamos que tiene uno cada uno de: 411, 741, 318. Determinar la combinación que producirá la mayor tasa de respuesta del sistema en la Figura\(\PageIndex{2}\).
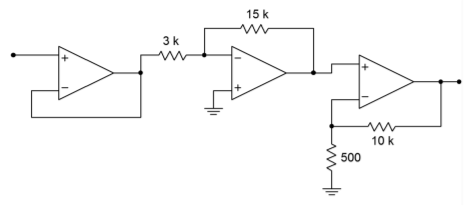
Figura\(\PageIndex{2}\)
35. Repita Problema 5.34 para producir el sistema más alto\(f_2\).
36. Suponiendo que la resistencia de la fuente impulsora es 0\(\Omega \) en la Figura 5.3.7. Determine el voltaje de ruido de salida si ambos dispositivos son 411.
37. Derivar la Ecuación 5.3.9 del texto.
Problemas de simulación por computadora
38. Usa un simulador para crear una parcela de Bode para Problem 5.10. Si un modelo macro para el LM318 no está disponible, utilice el 741 en su lugar.
39. Crear una representación en el dominio del tiempo de la tensión de salida del Problema 5.20 usando un simulador.
40. Crear una representación en el dominio del tiempo de la tensión de salida del Problema 5.21 usando un simulador. Repita la simulación usando un amplificador operacional LM318 en lugar del 741. ¿Qué indican los resultados?
41. Simular el circuito diseñado en Problema 5.26. Verificar\(f_2\) y\(A_v\) a través de una parcela de Bode.
42. Generar una gráfica Bode usando un simulador y verificar\(f_2\) y\(A_v\) para el circuito diseñado en Problema 5.29.
43. Generar una gráfica de Bode usando un simulador y verificar\(f_2\) para el circuito diseñado en Problema 5.35.