11.6: Realización de filtros prácticos

Por lo general, el diseño del filtro comienza con algunos parámetros básicos deseados. Esto generalmente incluye la frecuencia de ruptura, la cantidad de ondulación que puede tolerarse en la banda de paso (si la hay) y los niveles de atenuación deseados en puntos específicos en las bandas de transición y parada. También se puede especificar la respuesta de fase y los retardos de tiempo asociados. Si la respuesta de fase es primordial, normalmente se elige el Bessel. De igual manera, si no se puede permitir la ondulación de banda de paso, no se consideran Chebyshevs. Con el uso de curvas comparativas como las que se encuentran en las Figuras 11.4.1 a 11.5.2, se puede determinar el orden de filtro y la alineación a partir de los valores de atenuación requeridos. En este punto, el rendimiento del filtro estará completamente especificado, por ejemplo, un Butterworth de 1 kHz, paso bajo, de tercer orden. Hay muchas maneras en que se puede realizar esta especificación.

11.6.1: Filtros Sallen y Key VCVS

Hay muchas formas posibles de crear un filtro activo. Quizás las formas más populares para realizar filtros activos de paso alto y bajo son los modelos de fuente de voltaje controlado por voltaje Sallen y Key. Como su nombre lo indica, las formas Sallen y Key se basan en un VCVS; en otras palabras, utilizan retroalimentación negativa serie-paralela. Un circuito general para estos modelos se muestra en la Figura\(\PageIndex{1}\). Este circuito es una sección de dos polos (segundo orden) y se puede configurar para filtrado paso alto o bajo. Para nuestros propósitos, el bloque amplificador utilizará un amplificador operacional, aunque es posible un amplificador discreto. Además del amplificador, hay cuatro impedancias generales en el circuito. Por lo general, cada elemento es una sola resistencia o condensador. Como veremos, la selección del tipo de componente determinará el tipo de filtro.

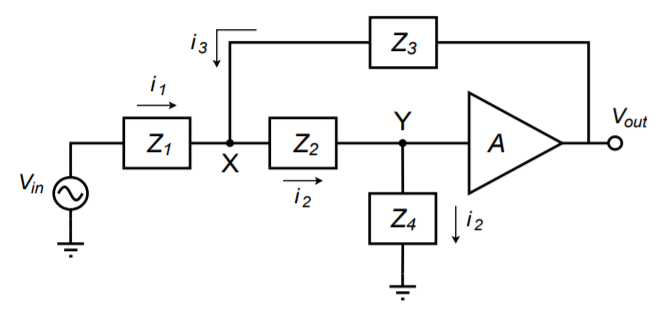
Figura\(\PageIndex{1}\): Sección de filtro general VCVS de 2 polos.

En este punto, necesitamos derivar la ecuación de transferencia general para el circuito. Una vez establecida la ecuación general, podremos afinar el circuito para casos especiales. Al ser un circuito activo de orden superior, este procedimiento será naturalmente algo más complicado que las derivaciones que se encuentran en el Capítulo Uno para las redes simples de plomo y lag de primer orden. Sin embargo, los conceptos son consistentes. Esta derivación utiliza un análisis ganglionar. Para que el análisis sea un poco más conveniente, ayudará si declaramos el voltaje\(V_y\) como 1 V. Esto nos salvará de llevar un factor de voltaje de entrada a través de nuestros cálculos, que de todos modos habría que factorizar fuera de la ecuación general. Por inspección observamos lo siguiente:

\[V_{out} = AV_y = A \label{11.1} \]

\[ i_1 = \frac{V_{in} − V_x}{Z_1} \nonumber \]

\[ i_2 = \frac{1}{Z_4} \label{11.2} \]

\[ i_3 = \frac{V_{out} − V_x}{Z_3} = \frac{A − V_x}{Z_3} \nonumber \]

\[V_x = i_2 Z_2 + V_y = i_2 Z_2 + 1 \label{11.3} \]

Por la ecuación de sustitución\ ref {11.2} en la ecuación\ ref {11.3}, se\(V_x\) puede expresar como

\[ V_x = \frac{Z_2}{Z_4} +1 \nonumber \]

Ahora sumamos las corrientes según la cifra,

\[ i_2 = i_1 + i_3 \nonumber \]

sustituir nuestras equivalencias actuales,

\[ \frac{1}{Z_4} = \frac{V_{in} − V_x}{Z_1} + \frac{A − V_x}{Z_3} \nonumber \]

y resolver la ecuación en términos de\(V_{in}\):

\[\frac{V_{in} − V_x}{Z_1} = \frac{1}{Z_4} − \frac{A − V_x}{Z_3} \\ V_{in} − V_x = \frac{Z_1}{Z_4} − \frac{Z_1 (A − V_x )}{Z_3} \\ V_{in} = \frac{Z_1}{Z_4} − \frac{Z_1 (A − V_x )}{Z_3} +V_x \\ V_{in} = \frac{Z_1}{Z_4} − \frac{Z_1 (A − V_x )}{Z_3} + \frac{Z_2}{Z_4} +1 \\ V_{in} = \frac{Z_1}{Z_4} − \frac{Z_1}{Z_3} \left( A − \frac{Z_2}{Z_4} −1 \right) + \frac{Z_2}{Z_4} +1 \\ V_{in} = \frac{Z_1}{Z_4} − \frac{Z_1}{Z_3} A+ \frac{Z_1 Z_2} {Z_3 Z_4} + \frac{Z_1}{Z_3} + \frac{Z_2}{Z_4} +1 \nonumber \]

\[V_{in} = \frac{Z_1}{Z_4} + \frac{Z_1}{Z_3} (1 − A) + \frac{Z_1 Z_2}{Z_3 Z_4} + \frac{Z_2}{Z_4} +1 \label{11.4} \]

Ahora podemos escribir nuestra ecuación general de transferencia usando Ecuaciones\ ref {11.1} y\ ref {11.4}.

\[\frac{V_{out}}{V_{in}} = \frac{A}{\frac{Z_1}{Z_4} + \frac{Z_1}{Z_3} (1 − A) + \frac{Z_1 Z_2}{Z_3 Z_4} + \frac{Z_2}{Z_4} +1} \label{11.5} \]

La ecuación\ ref {11.5} es aplicable a cualquier variación de la Figura\(\PageIndex{1}\) que queramos hacer. Todo lo que tenemos que hacer es sustituir los elementos de circuito apropiados por\(Z_1\) a través\(Z_4\). Como se puede adivinar, la sustitución directa de los valores de resistencia y reactancia haría un trabajo considerable. Para paliar esta dificultad, los diseñadores confían en la técnica de transformación de Laplace. Esto también se conoce como la técnica\(s\) de dominio. Un análisis detallado de la transformación de Laplace está más allá del alcance de este texto, pero cierta familiaridad resultará útil. La idea básica es sustituir términos complejos por otros más simples. Esto se realiza estableciendo la variable\(s\) igual a\(j\omega\). Como verás, esta sustitución lleva a derivaciones y ecuaciones de circuito mucho más simples y generalizadas. Una reactancia capacitiva se puede reducir de la siguiente manera.

\[\text{Capacitive Reactance } = − j X_C \nonumber \]

\[\text{Capacitive Reactance } = \frac{− j}{\omega C} \nonumber \]

\[\text{Capacitive Reactance } = \frac{1}{j\omega C} \nonumber \]

\[\text{Capacitive Reactance } = \frac{1}{sC} \nonumber \]

Por lo tanto, siempre que se necesita una reactancia capacitiva,\(1/ sC\) se usa la expresión. Las ecuaciones pueden ser manipuladas usando álgebra básica.

11.6.2: Filtros paso bajo Sallen y Key

Derivamos una expresión general basada en la Ecuación\ ref {11.5} para filtros de paso bajo. Un filtro de paso bajo es una red de lag, así que para hacer eco de esto, usaremos resistencias para los dos primeros elementos y condensadores para el tercero y cuarto. Usando el\(s\) operador encontramos,\(Z_1 = R_1\),\(Z_2 = R_2, Z_3 = 1/ sC1\), y\(Z_4 = 1/ sC2\).

\[\frac{V_{out}}{V_{in}} = \frac{A}{\frac{Z_1}{Z_4} + \frac{Z_1}{Z_3} (1 − A) + \frac{Z_1 Z_2}{Z_3 Z_4} + \frac{Z_2}{Z_4} +1} \nonumber \]

\[\frac{V_{out}}{V_{in}} = \frac{A}{sR_1C_2+s R_1C_1 (1−A)+s^2 R_1 R_2C_1C_2+s R_2C_2+1} \nonumber \]

\[\frac{V_{out}}{V_{in}} = \frac{A}{s^2 R_1 R_2C_1C_2+s(R_1C_2+R_2C_2+R_1C_1 (1−A))+1} \nonumber \]

La mayor potencia de\(s\) en el denominador determina el número de polos en el filtro. Debido a que este es un 2 aquí, el filtro debe ser de tipo 2 polos (segundo orden), como se esperaba. Por lo general, es más conveniente si el coeficiente denominador para\(s^2\) es unidad. Esto hace que la ecuación sea más fácil de factorial.

\[\frac{V_{out}}{V_{in}} = \frac{A/R_1R_2C_1C_2}{s^2+s( \frac{1}{R_2C_1} + \frac{1}{R_1C_1} + \frac{1}{R_2C_2} (1−A)) + \frac{1}{R_1R_2C_1C_2}} \label{11.6} \]

Los sistemas de segundo orden aparecen en una variedad de áreas incluyendo mecánica, acústica, hidráulica y eléctrica. Han sido ampliamente estudiadas, y una forma generalizada de un grupo de respuestas de segundo orden viene dada por

\[G = \frac{A\omega^2}{s^2+\alpha\omega s + \omega^2} \label{11.7} \]

donde\(A\) está la ganancia del sistema,\(\omega\) es la frecuencia resonante en radianes, y\(\alpha\) es el factor de amortiguación.

Al comparar la forma general de la Ecuación\ ref {11.7} con el filtro paso bajo Ecuación\ ref {11.6}, encontramos que

\[\omega^2 = \frac{1}{R_1 R_2C_1C_2} \label{11.8} \]

\[\alpha\omega = \frac{1}{R_2C_1} + \frac{1}{R_1C_1} + \frac{1}{R_2C_2} (1−A) \label{11.9} \]

Con base en la expresión general de la Ecuación\ ref {11.7}, podemos derivar ecuaciones para la magnitud de ganancia versus frecuencia y fase versus frecuencia, como hicimos en el Capítulo Uno para los sistemas de primer orden. Para la mayoría de los trabajos de filtro, es conveniente trabajar con frecuencia normalizada en lugar de una frecuencia verdadera. Esto significa que la frecuencia crítica se establecerá en 1 radián por segundo, y se desarrollará una ecuación generalizada. Para los circuitos que utilizan otras frecuencias críticas, se utiliza la ecuación general y sus resultados son simplemente escalados por un factor igual a esta nueva frecuencia. La versión normalizada de la ecuación\ ref {11.7} es

\[G = \frac{A}{s^2 + \alpha s + 1} \label{11.10} \]

Para determinar las expresiones de ganancia y fase, la Ecuación\ ref {11.10} debe dividirse en sus componentes real e imaginario. El primer paso es reemplazar\(s\) con su equivalente,\(j\omega\), para luego agrupar los componentes real e imaginario.

\[G = \frac{A}{( j\omega)^2 + j \alpha\omega+1} \nonumber \]

\[G = \frac{A}{−\omega^2 + j\alpha\omega+1} \nonumber \]

\[G = \frac{A}{(1−\omega^2 ) + j\alpha \omega} \nonumber \]

Para dividir esto en componentes reales e imaginarios separados, debemos multiplicar el numerador y el denominador por el complejo conjugado del denominador,\((1-\omega^2 ) - j\alpha\omega\).

\[G = \frac{A}{(1−\omega^2 ) + j\alpha\omega}\frac{(1−\omega^2 ) − j \alpha\omega}{(1−\omega^2 )− j \alpha\omega} \\ G = \frac{A((1−\omega^2 ) − j \alpha\omega)}{(1−\omega^2 )^2+\alpha^2 \omega^2} \nonumber \]

\[ G = \frac{A (1−\omega^2 )}{(1−\omega^2 )^2+\alpha^2\omega^2} − j \frac{A\alpha\omega}{(1−\omega^2 )^2+\alpha^2\omega^2} \label{11.11} \]

Para la magnitud de ganancia, recordemos que Mag =\(\sqrt{(real^2 + imaginary^2)}\). Aplicando la ecuación\ ref {11.11} a esta relación rinde

\[\text{Mag } = \sqrt{\left( \frac{A(1−\omega^2 )}{(1−\omega^2 )^2+\alpha^2 \omega^2} \right)^2 + \left( − \frac{A\alpha\omega}{(1 − \omega^2 )^2+\alpha^2\omega^2} \right)^2} \\ \text{Mag } = \sqrt{ \frac{A^2 (1−\omega^2 )^2}{((1−\omega^2 )^2 + \alpha^2 \omega^2 )^2} + \frac{A^2 \alpha^2 \omega^2}{((1−\omega^2 )^2 + \alpha^2 \omega^2 )^2}} \\ \text{Mag } = \frac{\sqrt{A^2 ((1−\omega^2 )^2+\alpha^2\omega^2 )}}{((1−\omega^2 )^2+\alpha^2 \omega^2 )^2} \\ \text{Mag } = \frac{A \sqrt{(1−\omega^2 )^2+\alpha^2 \omega^2}}{(1−\omega^2 )^2+\alpha^2 \omega^2} \\ \text{Mag } = \frac{A}{\sqrt{(1−\omega^2 )^2+\alpha^2 \omega^2}} \nonumber \]

\[\text{Mag } = \frac{A}{\sqrt{1 + \omega^2 (\alpha^2 − 2) + \omega^4}} \label{11.12} \]

Para la respuesta de fase, recordemos eso\(\theta = \tan^{−1}(imaginary / real)\). Aplicando la ecuación\ ref {11.11} a esta relación rinde

\[\theta = \arctan \frac{− \frac{A\alpha\omega}{(1−\omega^2 )^2 + \alpha^2 \omega^2}}{\frac{A(1−\omega^2 )}{ (1−\omega^2 )^2 + \alpha^2 \omega^2}} \\ \theta = \arctan \frac{−A\alpha\omega}{A(1−\omega^2 )} \nonumber \]

\[\theta = − \arctan \frac{\alpha\omega}{1−\omega^2} \label{11.13} \]

Para utilizar las Ecuaciones\ ref {11.12} y\ ref {11.13} con una alineación particular, sustituya el valor de amortiguación apropiado y simplifique. La derivación de factores específicos de amortiguación está fuera del alcance de este capítulo, pero se puede encontrar en textos especializados en diseño de filtros. Para nuestros propósitos, se presentarán tablas de factores de amortiguación para alineaciones específicas. Como un posible ejemplo, el factor de amortiguación para una alineación Butterworth de segundo orden es\(\sqrt{2}\). Sustituyendo esto en la Ecuación\ ref {11.12} produce

\[\text{Mag } = \frac{A}{\sqrt{1+\omega^2 (\alpha^2 − 2) + \omega^4}} \nonumber \]

\[\text{Mag } = \frac{A}{\sqrt{1+\omega^2 ((\sqrt{2})^2 −2) + \omega^4}} \nonumber \]

\[\text{Mag } = \frac{A}{\sqrt{1 + \omega^4}} \nonumber \]

Hay una gran cantidad de formas de configurar un filtro de paso bajo dadas las ecuaciones anteriores. Para que podamos poner cierta consistencia en lo que parece ser un desastre caótico, veremos dos variaciones distintas y útiles. Ellos son la realización igual componente y la realización de ganancia de unidad.

11.6.3: La versión de igual componente

Aquí, vamos a establecer\(R_1 = R_2\) y\(C_1 = C_2\). Para mantener la ecuación resultante genérica, utilizaremos una frecuencia normalizada de 1 radián por segundo. Para otras frecuencias de afinación, simplemente escalaremos nuestros resultados al valor deseado. De la Ecuación\ ref {11.8}\(\omega = 1\), si\(R_1R_2C_1C_2 = 1\), entonces, y la solución más sencilla sería establecer\(R_1 = R_2 = C_1 = C_2 = 1\) (unidades de ohmios y faradios). La ecuación\ ref {11.6} simplifica a

\[\frac{V_{out}}{V_{in}} = \frac{A}{s^2 + s(1+1+1(1 −A))+1} \nonumber \]

Tenga en cuenta que el factor de amortiguación ahora viene dado por

\[\alpha = 1+1+1(1−A) \nonumber \]

\[\alpha = 3 − A \nonumber \]

Vemos que la ganancia y la amortiguación del filtro están unidas entre sí. De hecho, para un cierto factor de amortiguación, solo una ganancia específica funcionará correctamente:

\[A = 3 − \alpha \nonumber \]

Como la ganancia de un amplificador no inversor es

\[A = 1 + \frac{R_f}{R_i} \nonumber \]

podemos encontrar el valor requerido para\(R_f\) combinando estas dos ecuaciones:

\[R_f = 2 − \alpha \nonumber \]

El prototipo terminado se muestra en la Figura\(\PageIndex{2}\).

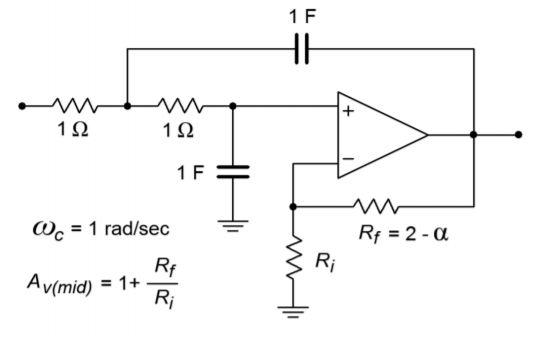
Figura\(\PageIndex{2}\): VCVS de paso bajo de igual componente.

11.6.4: La versión unidad-ganancia

Aquí vamos a establecer\(A = 1\), y\(R_1 = R_2\). De la Ecuación\ ref {11.8}, si\(\omega = 1\), entonces\(R_1R_2C_1C_2 = 1\), y por lo tanto\(C_1 = 1/C_2\). En efecto, la relación de los condensadores establecerá el factor de amortiguación para el sistema. La ecuación\ ref {11.6} puede simplificarse a

\[\frac{V_{out}}{V_{in}} = \frac{A}{s^2 + s( \frac{1}{C_1} + \frac{1}{C_1} ) + 1} \nonumber \]

El factor de amortiguación ahora viene dado por

\[\alpha = \frac{1}{C_1} + \frac{1}{C_1} \\ \alpha = \frac{2}{C_1} \text{ or,} \\ C_1 = \frac{2}{\alpha} \nonumber \]

Porque\(C_1 = 1/C_2\), encontramos

\[C_2 = \frac{\alpha}{2} \nonumber \]

El prototipo terminado se muestra en la Figura\(\PageIndex{3}\).

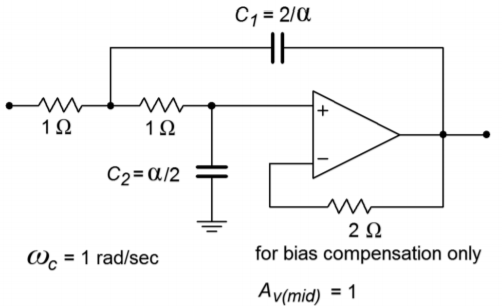
Figura\(\PageIndex{3}\): VCVS de ganancia unitaria de paso bajo.

Como puede ver, hay bastante similitud entre las dos versiones. Es importante tener en cuenta que las entradas a estos circuitos deben regresar a tierra a través de una ruta de CC de baja impedancia. Si la fuente de señal está acoplada capacitivamente, la corriente de polarización de entrada del amplificador operacional no se puede configurar correctamente y, por lo tanto, se debe usar alguna forma de resistencia de retorno de CC en la fuente. Además, puede ver que el factor de amortiguación (es decir, alineación) del filtro juega un papel en la configuración de los valores de los componentes. Si los valores mostrados se toman como unidades de ohmios y faradios, la frecuencia crítica será de 1 radián por segundo. Es una práctica aceptada normalizar las formas básicas de circuitos como estos, para que la frecuencia crítica funcione a este valor conveniente. Esto hace que sea muy fácil escalar los valores de los componentes para que se ajusten a la frecuencia crítica deseada. Debido a que la frecuencia crítica es inversamente proporcional a los valores de resistencia y condensador de sintonización, solo necesita encogerse\(R\) o\(C\) para aumentar\(f_c\). (Recuerda,\(f_c = 1/(2\pi RC))\). Un segundo paso de escalado normalmente sigue esto, con el fin de crear valores prácticos para\(R\) y\(C\). Este procedimiento se muestra mejor con un ejemplo.

Ejemplo\(\PageIndex{1}\)

Diseñe un filtro Butterworth de segundo orden y paso bajo de 1 kHz. Examine tanto la forma de componente igual como la unidad-ganancia tal como se dibuja en la Figura\(\PageIndex{2}\) y\(\PageIndex{3}\), respectivamente. El factor de amortiguación requerido es 1.414.

Empecemos con la versión de igual componente. Primero, encuentre el valor requerido para\(R_f\) a partir del factor de amortiguación, como se indica en el diagrama.

\ [R_f = 2 −\ alfa\\ R_F = 2 −1.414\\ R_F = 0.586\ O

mega\ nonumber\]

Tenga en cuenta que esto producirá una ganancia de banda de paso de

\[A_v = 1+ \frac{R_f}{R_i} \\ A_v = 1+ \frac{0.586}{1} \\ A_v = 1.586 \nonumber \]

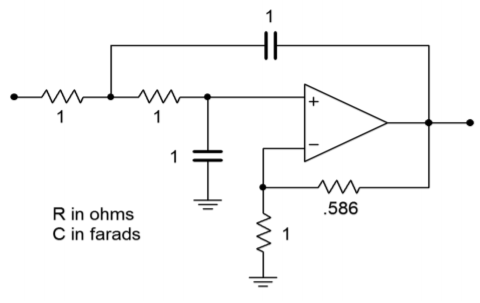
Figura\(\PageIndex{4}\): Cálculo de amortiguación inicial para Ejemplo\(\PageIndex{1}\) (versión de igual componente).

La figura\(\PageIndex{4}\) muestra el filtro de paso bajo Butterworth de segundo orden. Su frecuencia crítica es de 1 radián por segundo. Necesitamos escalar esto a 1 kHz.

\[\omega_c = 2\pi f_c \\ \omega_c = 2\pi 1 kHz \\ \omega_c = 6283 \text{ radians per second} \nonumber \]

Nuestra frecuencia crítica deseada es 6283 veces mayor que la base normalizada. Como\(\omega_c = 1/RC\), para traducir la frecuencia hacia arriba, todo lo que tenemos que hacer es dividir\(R\) o\(C\) por 6283. Realmente no importa cuál elijas, aunque generalmente es más fácil encontrar tamaños “impares” para resistencias que capacitores, así que usaremos\(R\).

\[R = \frac{1}{6283} \\ R = 1.59 \times 10^{−4} \Omega \nonumber \]

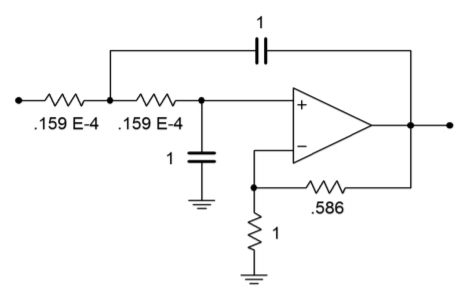
Figura\(\PageIndex{5}\): El filtro para Ejemplo\(\PageIndex{1}\) después del escalado de frecuencia (versión de igual componente).

La figura\(\PageIndex{5}\) muestra nuestro filtro Butterworth de 1 kHz, paso bajo y segundo orden. Como puede ver, sin embargo, los valores de los componentes no son muy prácticos. Por lo tanto, es necesario realizar las operaciones de escalado final. Primero, considere multiplicar\(R_f\) y\(R_i\) por 10 k. tenga en cuenta que esto no tendrá ningún efecto sobre la amortiguación, ya que es la relación de estos dos elementos lo que determina la amortiguación. Este escalado tampoco afectará a la frecuencia crítica, como lo\(f_c\) establecen las resistencias de sintonización y los capacitores. Segundo, necesitamos aumentar\(R\) a un valor razonable. Un factor de lo\(10^7\) colocará en\(1.59 k\Omega\). Para compensar, los capacitores de sintonización deben caer en una cantidad igual, lo que los lleva a 100 nF. El diseño terminado se muestra en la Figura\(\PageIndex{6}\). También se podrían utilizar otros factores de escalado. Además, si la compensación de sesgo es importante, los\(R_f\) valores\(R_i\) y deberán escalarse aún más, con el fin de equilibrar la resistencia vista en la entrada no inversora.

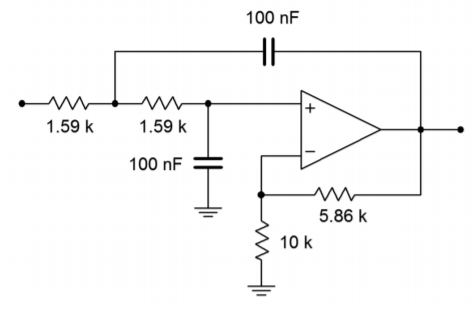
Figura Escala de impedancia\(\PageIndex{6}\) final para Ejemplo\(\PageIndex{1}\) (versión de igual componente).

El enfoque para la versión unidad-ganancia es similar. Primero, ajuste los valores del condensador para lograr el amortiguamiento deseado, como se especifica en la Figura\(\PageIndex{3}\).

\[C_1 = \frac{2}{\alpha} \\ C_1 = \frac{2}{1.414} \\ C_1 = 1.414 F \nonumber \]

\[C_2 = \frac{\alpha}{2} \\ C_2 = \frac{1.414}{2} \\ C_2 = 0.707 F \nonumber \]

El circuito resultante se muestra en la Figura\(\PageIndex{7}\). El circuito debe ser escalado a la deseada\(f_c\). El factor es 6283 una vez más, y el resultado se muestra en la Figura\(\PageIndex{8}\). El escalado final del componente se ve en la Figura\(\PageIndex{9}\).

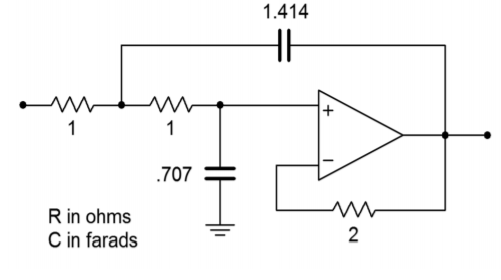
Figura Cálculo de amortiguación\(\PageIndex{7}\) inicial para Ejemplo\(\PageIndex{1}\) (versión unidad-ganancia).

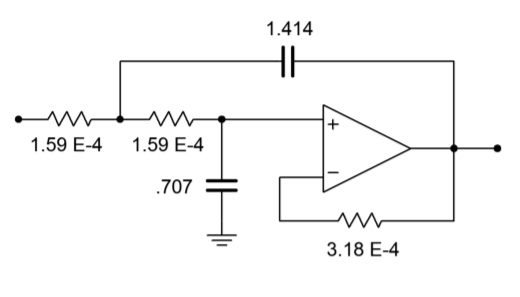
Figura\(\PageIndex{8}\) El filtro para Ejemplo\(\PageIndex{1}\) después del escalado de frecuencia (versión unidad-ganancia).

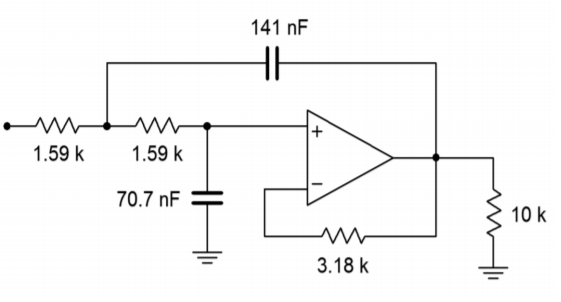
Figura Escala de impedancia\(\PageIndex{9}\) final para Ejemplo\(\PageIndex{1}\) (versión de ganancia unitaria).

Simulación por Computadora

En la Figura se muestra una simulación Multisim del diseño de filtro de Ejemplo\(\PageIndex{1}\)\(\PageIndex{10}\). El análisis muestra la gráfica Bode, que va desde 50 Hz hasta mejor que 20 kHz. Esto produce más de una década a cada lado de la frecuencia crítica de 1 kHz. El gráfico muestra claramente el punto −3 dB a aproximadamente 1 kHz, con una pendiente de atenuación de −12 dB por octava. Dado que esta es la versión de ganancia unitaria, la ganancia de baja frecuencia se establece en 0 dB. Además, tenga en cuenta que no hay picos evidentes en la curva de respuesta, como se espera para una alineación de Butterworth. También se muestra la respuesta de fase. Algunas herramientas gráficas continúan el desplazamiento de fase por debajo de −180 grados, mientras que otras lo voltearán a +180, como lo hace Multisim. Tenga en cuenta que si se extiende el rango de la gráfica de frecuencias, el desplazamiento de fase comienza a aumentar en las frecuencias más altas en lugar de nivelarse. Esto se debe al desplazamiento de fase extra producido por el amplificador operacional a medida que se acerca la frecuencia de operación\(f_{unity}\). Un modelo de amplificador operacional más simple no crearía este efecto del mundo real.

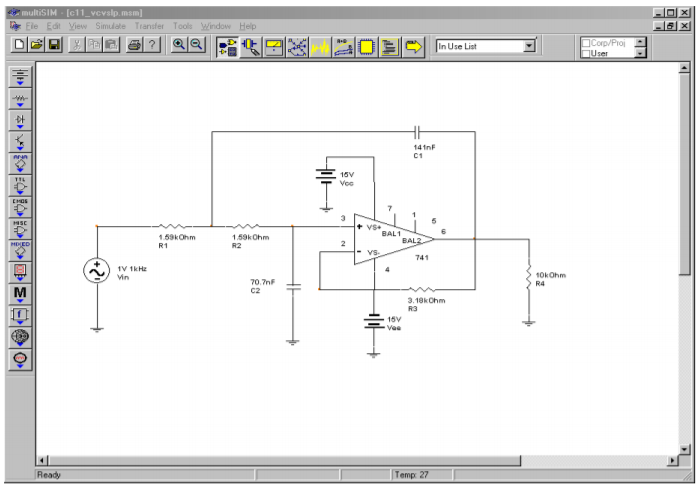
Figura Figura\(\PageIndex{10a}\): Filtro paso bajo VCVS en Multisim.

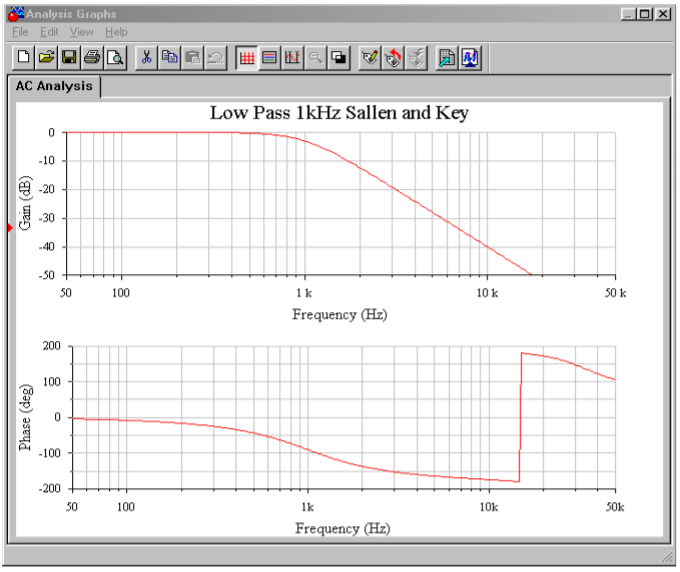
Figura Figura\(\PageIndex{10b}\): Gráficas de ganancia y fase para filtro paso bajo VCVS.

Finalmente, se utiliza un análisis de Monte Carlo para imitar los efectos observados debido a la tolerancia de componentes en un ambiente de producción (en este ejemplo, aproximadamente 10 por ciento de variación nominal para cada componente). Se generaron un total de 10 corridas. Si bien la forma general de la curva sigue siendo consistente, existe cierta variación en la frecuencia de las esquinas, sin duda más que el 10 por ciento que ofrece cualquier componente individual. Como puedes adivinar, un análisis de Montecarlo es muy tedioso de hacer a mano, pero bastante sencillo de configurar en un simulador.

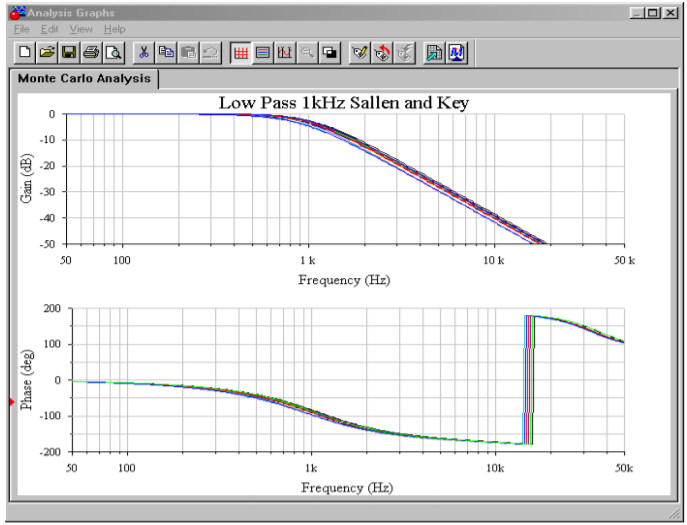
Figura Figura\(\PageIndex{10c}\): Análisis de Monte Carlo para filtro paso bajo VCVS.

Como puede ver, el proceso de realización es poco más que una secuencia de escalado. Esto hace que el diseño del filtro sea muy rápido. El funcionamiento de los filtros de paso alto es esencialmente el mismo.

11.6.5: Filtros paso alto Sallen y Key

Podemos derivar una expresión general para filtros de paso alto, basada en la Ecuación\ ref {11.5}. Un filtro de paso alto es una red de conductores, por lo que para hacer eco de esto, usaremos condensadores para los dos primeros elementos y resistencias para el tercero y cuarto. Usando el\(s\) operador, encontramos,\(Z_1 = 1/sC1\),\(Z_2 = 1/sC2\),\(Z_3 = R_1\), y\(Z_4 = R_2\).

\[\frac{V_{out}}{V_{in}} = \frac{A}{\frac{Z_1}{Z_4} + \frac{Z_1}{Z_3} (1−A)+ \frac{Z_1Z_2}{Z_3Z_4} + \frac{Z_2}{Z_4} +1} \\ \frac{V_{out}}{V_{in}} = \frac{A}{\frac{1}{s R_2C_1} + \frac{1}{s R_1C_1} (1−A) + \frac{1}{s^2 R_1 R_2C_1C_2} + \frac{1}{s R_2C_2} +1} \nonumber \]

\[ \frac{V_{out}}{V_{in}} = \frac{A s^2}{s^2+s( \frac{1}{R_2C_1} + \frac{1}{R_2C_2} + \frac{1}{R_1C_1} (1−A)) + \frac{1}{R_1R_2C_1C_2}} \label{11.14} \]

Al igual que con los filtros de paso bajo tenemos dos realizaciones básicas: igual componente y unidad-ganancia. En ambos casos, comenzamos con la Ecuación\ ref {11.14} y usamos frecuencia normalizada (1 radián por segundo). Las derivaciones son muy similares al caso de paso bajo, y los resultados se resumen a continuación. La versión de igual componente:

\[\alpha = 3 −A \nonumber \]

La versión de ganancia de unidad:

\[R_2 = \frac{2}{\alpha} \\ R_1 = \frac{\alpha}{2} \nonumber \]

Estas formas se muestran en las Figuras Figura\(\PageIndex{11}\) y Figura\(\PageIndex{12}\). Puede que en este punto haga dos preguntas: Una, ¿cómo encuentra el factor de amortiguación y dos, qué pasa con los filtros de orden superior?

Para encontrar el factor de amortiguación necesario, se\(\PageIndex{13}\) puede consultar un gráfico como Figura Figura. Esta tabla también introduce un nuevo ítem, y ese es el factor de frecuencia,\(k_f\). Normalmente, la frecuencia crítica y la frecuencia descendente de 3 dB (frecuencia de ruptura) de un filtro no son del mismo valor. Son idénticos solo para la alineación Butterworth.

Para cualquier otra alineación, la frecuencia de ruptura deseada debe traducirse primero a la frecuencia crítica apropiada antes de realizar el escalado. Esto se ilustra en el siguiente ejemplo.

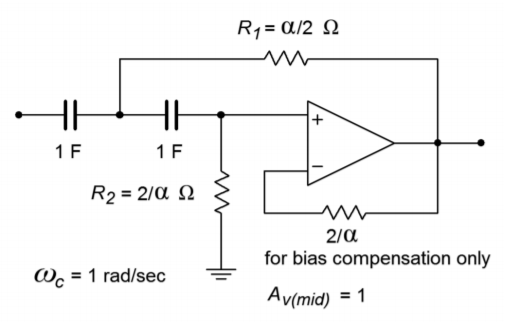
Figura Figura\(\PageIndex{11}\): VCVS de ganancia de unidad de paso alto.

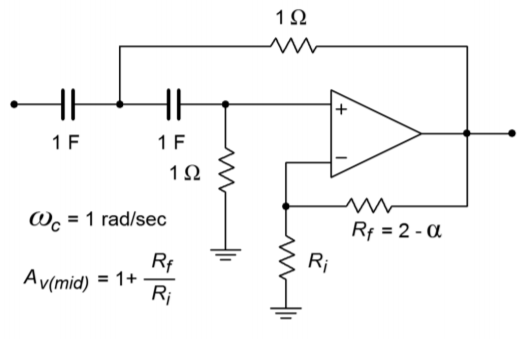
Figura Figura\(\PageIndex{12}\): VCVS de paso alto de igual componente.

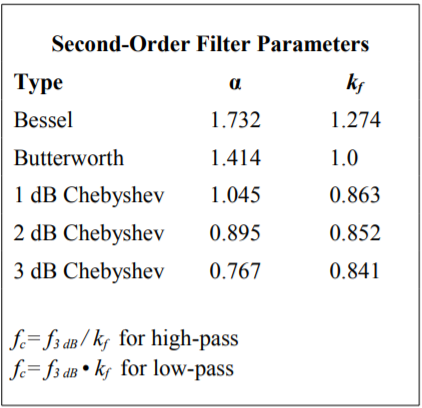
Figura Figura\(\PageIndex{13}\): Parámetros de filtro de segundo orden. De Lancaster, Don, Active Filter Cookbook, Segunda edición, Novedades1996. Reimpreso con permiso

Ejemplo\(\PageIndex{2}\)

Diseñe un filtro Bessel de paso alto de segundo orden, con una frecuencia\((f_{3dB})\) de rotura de 5 kHz.

Para este ejemplo, usemos la forma de unidad-ganancia que se muestra en la Figura Figura\(\PageIndex{11}\). Primero, obtener los factores de amortiguación y frecuencia de la Figura Figura\(\PageIndex{13}\).

\[k_f = 1.274, \text{ damping } = 1.732. \nonumber \]

Usando el factor de amortiguación, se pueden encontrar las dos resistencias de sintonización:

\[R_1 = \frac{\alpha}{2} \\ R_1 = \frac{1.732}{2} \\ R_1 = .866\Omega \nonumber \]

\[R_2 = \frac{2}{\alpha} \\ R_2 = \frac{2}{1.732} \\ R_2 = 1.155\Omega \nonumber \]

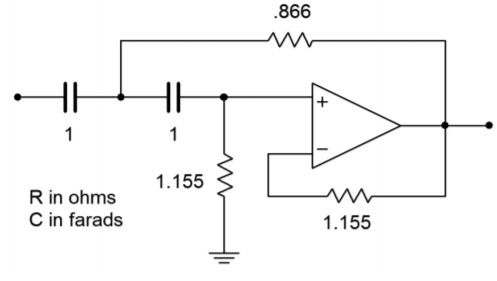
Figura Figura\(\PageIndex{14}\): Cálculo de amortiguación inicial para Ejemplo\(\PageIndex{2}\).

El resultado intermedio se muestra en la Figura Figura\(\PageIndex{14}\). Para hacer el escalado de frecuencia, la frecuencia de ruptura deseada de 5 kHz debe traducirse primero a la frecuencia crítica requerida. Debido a que se trata de un filtro de paso alto,

\[f_c = \frac{f_{3dB}}{k_f} \\ f_c = \frac{5 kHz}{1.274} \\ f_c = 3925 Hz \nonumber \]

\[\omega_c = 2\pi f_c \\ \omega_c = 2\pi 3925 \\ \omega_c = 24.66 k \text{ radians per second} \nonumber \]

Las resistencias de sintonización o los capacitores ahora pueden ser escalados.

\[R_1 = \frac{.866}{24.66 k} \\ R_1 = 3.51 \times 10^{−5} \Omega \nonumber \]

\[R_2 = \frac{1.155}{24.66 k} \\ R_2 = 4.68 \times 10^{−5} \Omega \nonumber \]

Ahora tenemos un filtro Bessel de 5 kHz, paso alto de segundo orden. Esto se muestra en la Figura Figura\(\PageIndex{15}\). Una escala final de nos\(10^8\) dará valores razonables, y se muestra en la Figura Figura\(\PageIndex{16}\).

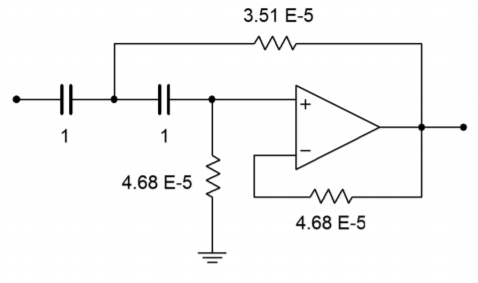
Figura Figura\(\PageIndex{15}\): Escalado de frecuencia para Ejemplo\(\PageIndex{2}\).

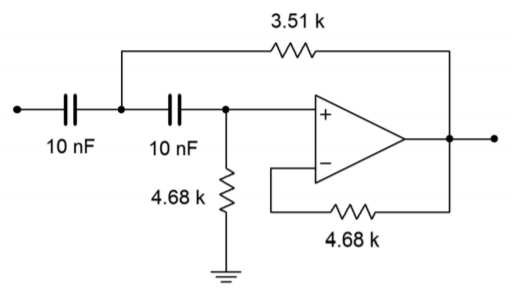
Figura Figura\(\PageIndex{16}\): Escala de impedancia por ejemplo\(\PageIndex{2}\).

11.6.6: Filtros de Orden Superior

Existe una idea errónea común entre los diseñadores de filtros novatos de que los filtros de orden superior pueden producirse mediante la conexión en cascada de varios filtros de orden inferior del mismo tipo. Esto no es cierto. Por ejemplo, la cascada de tres filtros Butterworth de 10 kHz de segundo orden no producirá} un filtro Butterworth de 10 kHz de sexto orden. Una inspección rápida revela por qué no es así: Un solo filtro de cualquier orden mostrará una pérdida de 3 dB en su frecuencia de ruptura por definición (en este caso, 10 kHz). Si tres filtros del mismo tipo están en cascada, cada filtro producirá una pérdida de 3 dB a la frecuencia de ruptura, lo que significa que se produce una pérdida total de 9 dB. Esto es cierto: un filtro de orden superior requerirá una serie de secciones individuales, cada una con factores específicos de amortiguación y frecuencia. Cada sección se basará en los formularios de segundo orden ya examinados. ¹ Para hacer filtros impares, introduciremos un filtro simple de un solo polo. Las versiones de paso alto y bajo de esta unidad se muestran en la Figura Figura\(\PageIndex{17}\). El factor de amortiguación para este circuito es siempre la unidad. Al trabajar con él, solo necesita preocuparse por el factor de frecuencia.

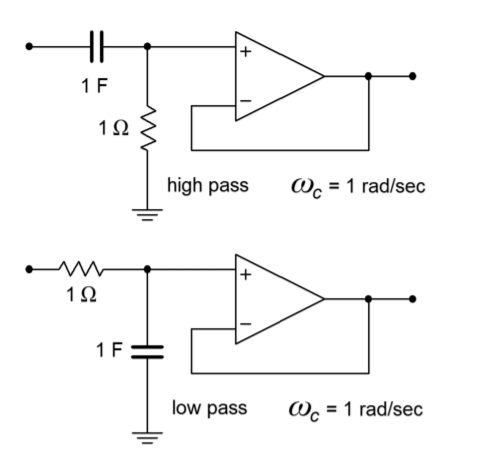
Figura Figura\(\PageIndex{17}\): Secciones unipolares.

Diseñar filtros de orden superior no es, conceptualmente, diferente a diseñar filtros de segundo orden. La realidad es que se necesitan nuevos gráficos para los factores de amortiguación y frecuencia requeridos. Un conjunto de gráficos compatibles se muestra en la Figura Figura\(\PageIndex{18}\) para los pedidos 3 a 6 en las siguientes páginas. Luego se presenta un ejemplo para mostrar el flujo de secuencia de diseño.

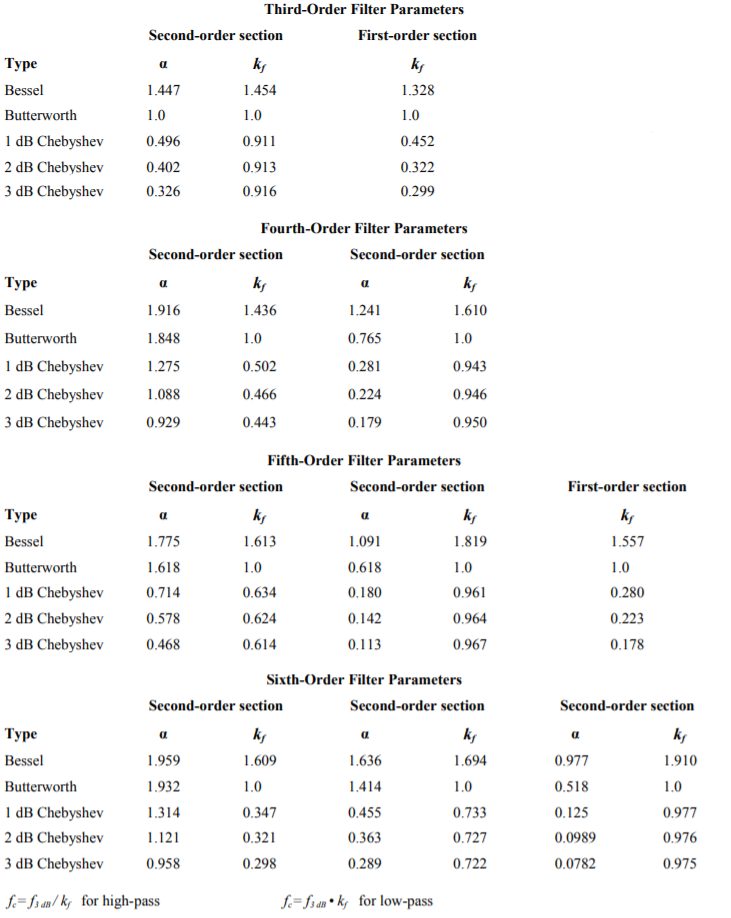
Figura\(\PageIndex{18a}\): Herramientas de diseño de filtros Parámetros para filtros de tercer a sexto orden. De Lancaster, Don, Active Filter Cookbook, Segunda edición, Novedades1996. Reimpreso con permiso

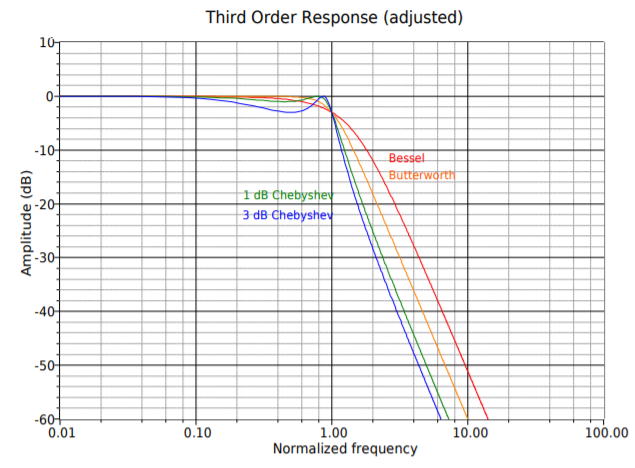
Figura\(\PageIndex{18b}\): Herramientas de diseño de filtros, respuesta continuada de tercer orden (ajustada).

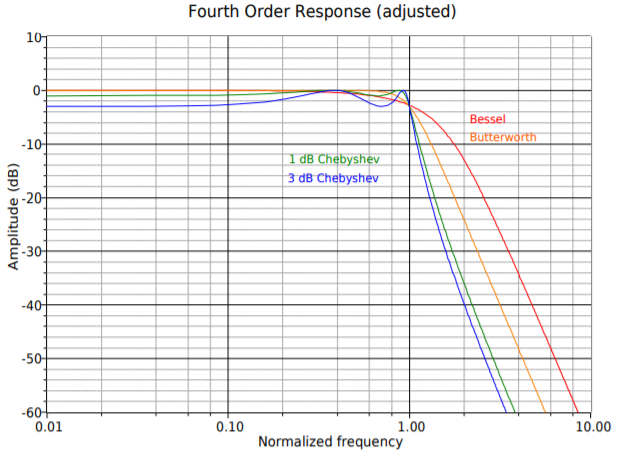
Figura\(\PageIndex{18c}\): Herramientas de diseño de filtros, respuesta continua de cuarto orden (ajustada).

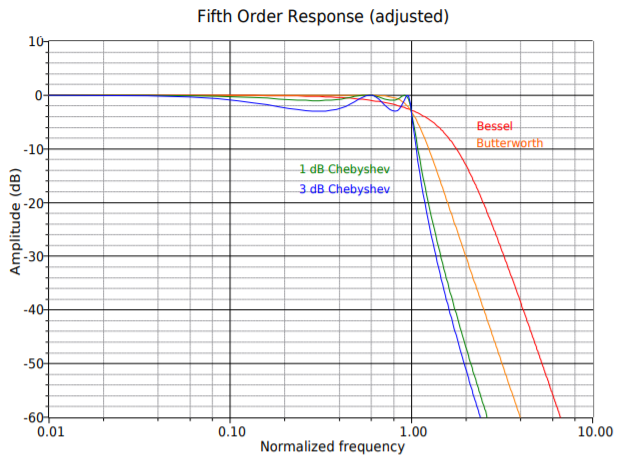
Figura\(\PageIndex{18d}\): Herramientas de diseño de filtros, respuesta continua de quinto orden (ajustada).

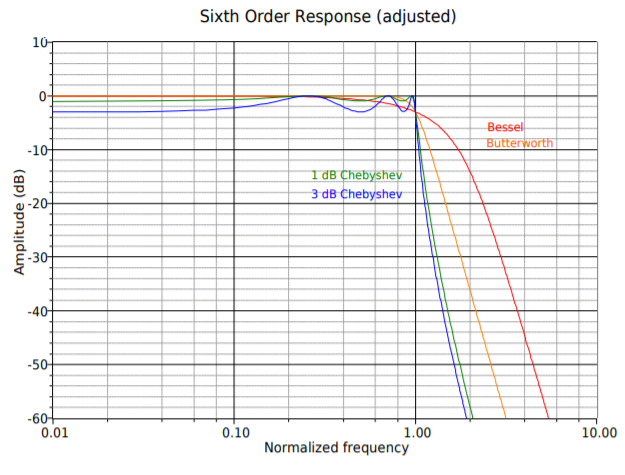
Figura\(\PageIndex{18e}\): Herramientas de diseño de filtros, respuesta continua de sexto orden (ajustada).

Ejemplo\(\PageIndex{3}\)

Deseamos diseñar un filtro adecuado para eliminar tonos subsónicos de un sistema estéreo. Esto podría usarse para reducir el ruido de la plataforma giratoria en un sistema vintage de alta fidelidad o DJ, o para reducir la vibración del escenario en un sistema de megafonía. El filtro debe atenuar las frecuencias por debajo del límite inferior de la audición humana (aproximadamente 20 Hz), al tiempo que permite que pasen todas las frecuencias más altas. La respuesta transitoria puede ser importante aquí, así que elegiremos una alineación de Bessel. También especificaremos un sistema de quinto orden. Esto creará una atenuación de aproximadamente 15 dB, una octava por debajo de la frecuencia de ruptura.

Primero, tenga en cuenta que la especificación requiere el uso de un filtro de paso alto. Este filtro puede realizarse con las formas de igual componente o unidad-ganancia. Como este diseño requerirá múltiples secciones, puede resultar una ganancia excesiva de la versión de igual componente. Nuestro sistema de quinto orden estará compuesto por dos secciones de segundo orden y una sección de primer orden. En la Figura se muestra una visión general del diseño\(\PageIndex{19}\), con los factores de amortiguación y frecuencia apropiados tomados de la Figura\(\PageIndex{18}\). Desglosaremos el análisis etapa por etapa.

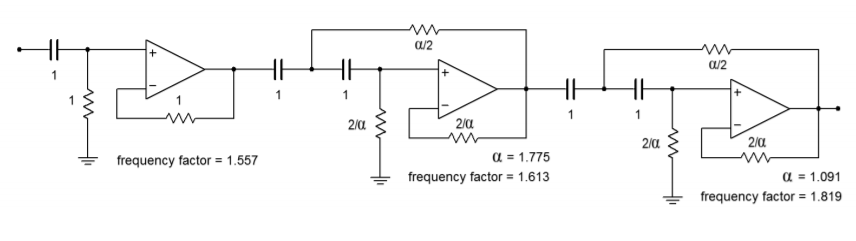
Figura\(\PageIndex{19}\): Esquema del circuito (Nota: todos los valores en ohmios y faradios).

Primero, encuentra la frecuencia de ruptura deseada en radianes.

\[\omega_{3dB} = 2 \pi f_{3dB} \\ \omega_{3dB} = 2 \pi 20 Hz \\ \omega_{3dB} = 125.7 \text{ radians per second} \nonumber \]

Etapa 1:

La frecuencia de ruptura debe traducirse a la frecuencia crítica requerida. Debido a que este es un filtro de paso alto, necesitamos dividirlo por el factor de frecuencia.

\[\omega_c = \frac{\omega_{3dB}}{k_f} \\ \omega_c = \frac{125.7}{1.557} \\ \omega_c = 80.7 \text{ radians per second} \nonumber \]

Escalaremos la resistencia en 80.7 para lograr esta frecuencia de sintonización.

\[R = \frac{1}{80.7} \\ R = .0124 \Omega \nonumber \]

\(C\)Los valores\(R\) y ahora deben escalarse para valores prácticos. Un factor de\(10^6\) sería razonable. El resultado final es

\[R = 12.4 k \\ C = 1\mu F \nonumber \]

Etapa 2:

Primero, determinar los valores para las dos resistencias a partir del factor de amortiguación dado.

\[R_1 = \frac{\alpha}{2} \\ R_1 = \frac{1.775}{2} \\ R_1 = 0.8875\Omega \nonumber \]

\[R_2 = \frac{2}{\alpha} \\ R_2 = \frac{2}{1.775} \\ R_2 = 1.127\Omega \nonumber \]

Ahora la frecuencia de ruptura debe traducirse a la frecuencia crítica requerida.

\[\omega_c = \frac{\omega_{3dB}}{k_f} \\ \omega_c = \frac{125.7}{1.613} \\ \omega_c = 77.9 \text{ radians per second} \nonumber \]

Escalaremos las resistencias en 77.9 para lograr esta frecuencia de sintonización.

\[R_1 = \frac{0.8875}{77.9} \\ R_1 = 0.0114\Omega \nonumber \]

\[R_2 = \frac{1.127}{77.9} \\ R_2 = 0.0145\Omega \nonumber \]

Nuevamente,\(R\) y\(C\) debe ser escalado para valores prácticos. Un factor de\(10^6\) sería razonable. El resultado final es

\[R_1 = 11.4k \\ R_2 = 14.5 k \\ C = 1\mu F \nonumber \]

Etapa 3:

Primero, determinar los valores para las dos resistencias a partir del factor de amortiguación dado.

\[R_1 = \frac{\alpha}{2} \\ R_1 = \frac{1.091}{2} \\ R_1 = 0.5455\Omega \nonumber \]

\[R_2 = \frac{2}{\alpha} \\ R_2 = \frac{2}{1.091} \\ R_2 = 1.833\Omega \nonumber \]

Ahora la frecuencia de ruptura debe traducirse a la frecuencia crítica requerida.

\[\omega_c = \frac{\omega_{3dB}}{k_f} \\ \omega_c = \frac{125.7}{1.819} \\ \omega_c = 69.1 \text{ radians per second} \nonumber \]

Escalaremos las resistencias en 69.1 para lograr esta frecuencia de sintonización.

\[R_1 = \frac{.5455}{69.1} \\ R_1 = 7.89 \times 10^{−3}\Omega \nonumber \]

\[R_2 = \frac{1.833}{69.1} \\ R_2 = 0.0265\Omega \nonumber \]

Nuevamente,\(R\) y\(C\) debe ser escalado para valores prácticos. Un factor de\(10^6\) sería razonable. El resultado final es

\[R_1 = 7.89 k\Omega \\ R_2 = 26.5 k\Omega \\ C = 1\mu F \nonumber \]

El diseño completo se muestra en la Figura\(\PageIndex{20}\). Tenga en cuenta que todos los condensadores están establecidos en\(1 \mu F\). Esto ciertamente ayuda a reducir el inventario y la colocación de piezas

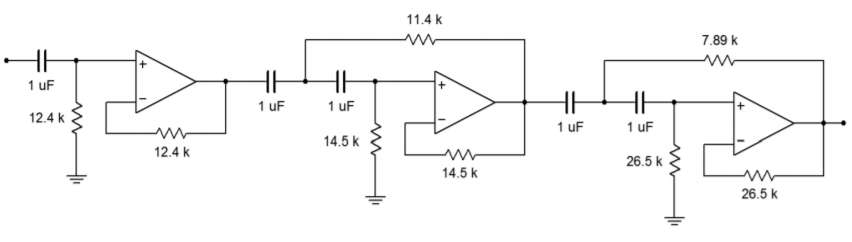
Figura Filtro\(\PageIndex{20}\) completado para Ejemplo\(\PageIndex{3}\).

Completaremos nuestra discusión sobre los filtros VCVS de paso alto y bajo con el siguiente ejemplo.

Ejemplo\(\PageIndex{4}\)

Como se mencionó anteriormente, es común que los sistemas de altavoces confíen en filtros pasivos para crear sus redes cruzadas. Las aplicaciones más exigentes como el monitoreo de estudio de grabación o los grandes sistemas de megafonía (es decir, sistemas de conciertos) no pueden permitirse las pérdidas asociadas con los crossovers pasivos.

En cambio, estas aplicaciones utilizan cruces activos compuestos por filtros activos, como el que se muestra en la Figura\(\PageIndex{21}\). Antes de que la señal de audio se alimente a un amplificador de potencia, se divide en dos o más bandas de frecuencia. Cada una de las señales resultantes alimenta su propia sección de amplificador de potencia/altavoz.

Figura\(\PageIndex{21}\): Crossover electrónico comercial. Reimpreso cortesía de Furman Sound, Inc.

Un diagrama de bloques de este enfoque se muestra en la Figura\(\PageIndex{22}\). Este es un sistema de dos vías. Los sistemas de refuerzo de sonido de concierto grandes pueden dividir el espectro de audio en cuatro o cinco segmentos. El sistema resultante será sin duda caro, pero mostrará menor distorsión y mayores niveles de salida que un sistema pasiblemente cruzado. Un sistema típico de dos vías podría cruzarse a 800 Hz. Es decir, las frecuencias superiores a 800 Hz se enviarán a un transductor especializado de alta frecuencia, mientras que las frecuencias por debajo de 800 Hz se enviarán a un transductor especializado de baja frecuencia. En esencia, la red crossover es una combinación de un filtro de paso bajo de 800 Hz y un filtro de paso alto de 800 Hz. El orden de los filtros y la alineación varían considerablemente dependiendo de la aplicación. Diseñemos un crossover de 800 Hz con filtros Butterworth de segundo orden.

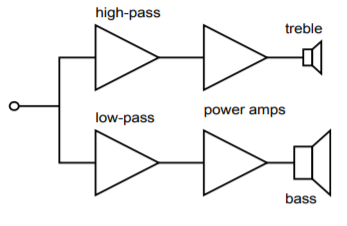
Figura\(\PageIndex{22}\): Sistema de crossover electrónico.

La disposición básica del circuito se muestra en la Figura\(\PageIndex{23}\). Estamos usando la versión de valor equalcomponent aquí. La ganancia exacta normalmente no es un problema en este caso, ya que se necesita agregar alguna forma de control de volumen de todos modos, para compensar entre la sensibilidad de los transductores de baja y alta frecuencia. (Esto se produce más fácilmente agregando un simple divisor/potenciómetro de voltaje en la salida de los filtros).

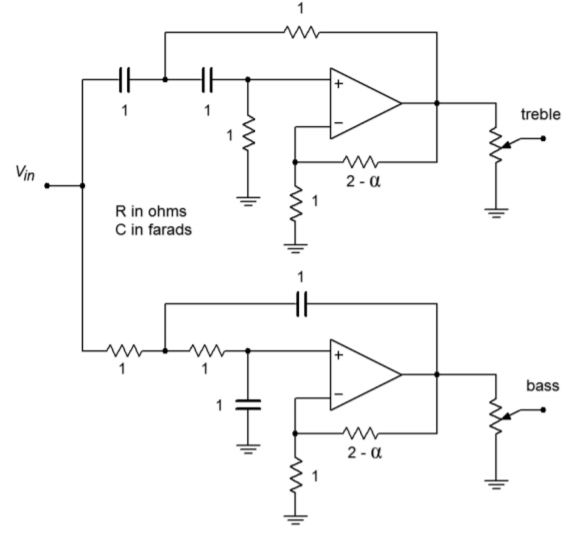
Figura\(\PageIndex{23}\): Secciones filtrantes básicas para cruce de Ejemplo\(\PageIndex{4}\).

Para los filtros Butterworth de segundo orden, se encuentra que el factor de amortiguación es 1.414, y el factor de frecuencia es la unidad (lo que indica que\(f_c\) y\(f_{3dB}\) son los mismos). Tenga en cuenta que el diseño para ambas mitades es casi el mismo. Ambas secciones muestran una\(f_c\) de 800 Hz, y un factor de amortiguación de 1.414. Con características idénticas, se deduce que los valores de los componentes serán los mismos en ambos circuitos.

El valor requerido para\(R_f\) es

\[R_f = 2 − \alpha \\ R_f = 2 −1.414 \\ R_f = 0.586\Omega \nonumber \]

La frecuencia crítica en radianes es

\[\omega_c = 2\pi f_c \\ \omega_c = 2\pi 800 Hz \\ \omega_c = 5027 \text{ radians per second} \nonumber \]

Nuevamente, escalaremos las resistencias de afinación para ceder

\[R = \frac{1}{5027} \\ R = 1.989 \times 10^{−4} \Omega \nonumber \]

Un\(RC\) escalado final por\(10^8\) produce

\[R = 19.9 k\Omega \\ C = 10 nF \nonumber \]

\(R_i\)y\(R_f\) se escalan por\(10 k\), y se pueden usar potenciómetros de conicidad de\(10 k\Omega\) tronco para los recortadores de volumen de salida. El circuito resultante se muestra en la Figura\(\PageIndex{24}\).

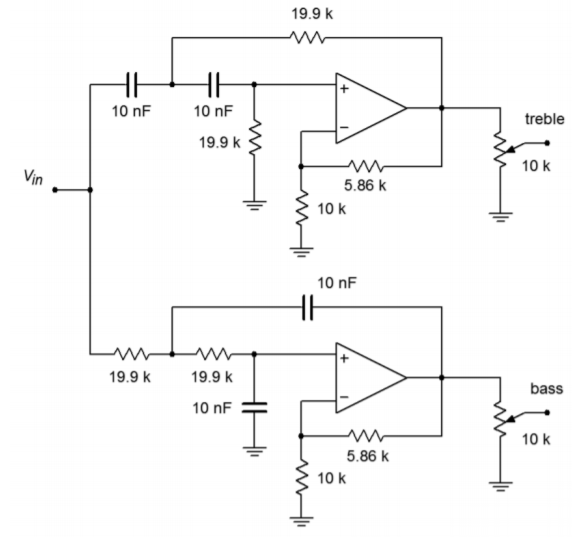
Figura\(\PageIndex{24}\): Diseño cruzado terminado por Ejemplo\(\PageIndex{4}\).

Referencias

¹ La función de transferencia de un filtro de orden superior contiene un polinomio de orden superior en el denominador de la forma\(s^n + b_{n−1} s^{n−1} + \dots + b_1 s + b_0\). El\(n\) indica el orden del filtro y los\(b\) coeficientes determinan la alineación. Este polinomio se factoriza en un producto de expresiones de segundo orden (con una posible unidad de primer orden para sistemas de orden impar). Cada una de estas expresiones corresponde a una sola sección en el filtro más grande.