2.6: Costo de energía y duración de la batería
- Page ID
- 86084
Como hemos visto, conocer las demandas de voltaje y corriente de un dispositivo dado nos permite determinar su potencia nominal y consumo de energía. Los siguientes pasos son determinar el costo de operar un dispositivo y, si funciona con batería, cuánto tiempo durará el dispositivo antes de necesitar baterías nuevas.
Costo de energía informática
Una vez que conocemos la potencia extraída por el dispositivo y por cuánto tiempo se utilizará, se puede determinar el costo para operar un dispositivo dado el costo por unidad de energía. A pesar de que mucha gente se refiere a su proveedor local de electricidad como “la compañía eléctrica”, no compramos “energía”, per se. Más bien, se nos factura la energía. Si bien sería posible determinar el costo por julio (o más prácticamente, por megajuulo), los proveedores normalmente facturan en base a kilovatios-hora, o kWh, el producto de la potencia y el tiempo 1. Esta unidad se utiliza porque la mayoría de los dispositivos y electrodomésticos residenciales y comerciales están clasificados en términos de consumo de energía en vatios. Al multiplicar el consumo de energía en vatios por el tiempo que se usa el dispositivo en horas, se obtiene un valor de vatios-hora. Esto es luego escalado por un factor de mil para llegar a kWh. Por ejemplo, un horno tostador de 1500 vatios utilizado durante 30 minutos (es decir, 0.5 horas) produce 750 vatios-hora, o 0.75 kWh. Finalmente, conociendo el costo por kWh, una simple multiplicación arroja el costo de la electricidad. Así, si la utilidad cobra 10 centavos por kWh, entonces el costo para hacer funcionar ese horno tostador es de 7.5 centavos. Si se usa durante una hora completa entonces cuesta 15 centavos, y así sucesivamente.
Para poner el uso en perspectiva, un hogar típico en Estados Unidos o Canadá usa alrededor de 900 kWh al mes, mientras que los hogares en muchos países de Europa podrían usar de la mitad a la cuarta parte de esa cantidad. La generación global de electricidad es de alrededor de 25 millones de gigavatios-hora al año. Las tarifas eléctricas típicas en Estados Unidos oscilan entre diez y veinte centavos por kWh, dependiendo de la región geográfica y el sector (por ejemplo, residencial o comercial).
Una bombilla incandescente de 100 vatios se deja encendida durante 24 horas. Si el costo de la electricidad es de 15 centavos por kWh, determine el costo para hacer funcionar la luz.
\[Cost = P \times t \times rate \nonumber \]
\[Cost = 100 W \times 24 hours \times 0.15 \$/kWh \nonumber \]
\[Cost = \$ 0.36 \nonumber \]
En este punto, debería ser obvio que cuanto más eficiente sea un dispositivo, menos costoso será funcionar. De hecho, es muy posible que a la larga, un dispositivo que es más caro que un dispositivo similar, aunque menos eficiente, pueda ser considerablemente menos costoso de usar a lo largo de su vida útil. Un buen ejemplo es una comparación entre una bombilla de luz incandescente ordinaria y una luz LED. La iluminación LED puede ser un orden de magnitud más eficiente que la iluminación incandescente. De hecho, las bombillas incandescentes pueden convertir menos del cinco por ciento de su entrada en una salida de luz utilizable, el 95 por ciento restante simplemente convirtiéndose en calor. Si bien son menos costosos de comprar inicialmente, su costo operativo es mucho mayor. Una forma adecuada de comparar las luces es examinar su salida de luz en lúmenes, no su consumo de energía. Por ejemplo, una luz incandescente de 60 vatios produce alrededor de 800 lúmenes de iluminación. Ese mismo nivel de iluminación se puede obtener con un dibujo LED de apenas 9 vatios. Además, normalmente las luces LED duran de diez a veinte veces más que las bombillas incandescentes.
Esto se ilustrará en el siguiente ejemplo.
Una cierta luz LED de 14 vatios produce la misma iluminación que una bombilla incandescente de 75 vatios. Asumir que el LED cuesta $11 y tiene una vida útil esperada de 15,000 horas. El incandescente cuesta 50 centavos cada uno y tiene una vida esperada de 1000 horas. Si el costo de la electricidad es de 12 centavos por kWh, determine el costo para ejecutar cada versión por 15,000 horas.
En primer lugar, cabe señalar que se necesitarán 15 bombillas incandescentes. A 50 centavos cada uno, eso es $7.50 para las bombillas. El costo para ejecutarlos es,
\[Cost = P \times t \times rate \nonumber \]
\[Cost = 75 W \times 15000 hours \times 0.12 \$/kWh \nonumber \]
\[Cost = \$ 135.00 \nonumber \]
El total es de 142.50 dólares. Ahora para el solo LED requerido:
\[Cost = P \times t \times rate \nonumber \]
\[Cost = 14 W \times 15000 hours \times 0.12 \$/kWh \nonumber \]
\[Cost = \$ 25.20 \nonumber \]
El total es de 36.20 dólares, un ahorro considerable, por no hablar de otros factores positivos entre ellos solo tener que cambiar la luz una vez en lugar de quince veces; una reducción considerable de la energía desperdiciada, disminuyendo así la demanda y el impacto ambiental; y finalmente, una reducción en las bombillas quemadas para una mayor disminución del impacto ambiental (reducción de flujo de residuos).
Baterías
Una batería es un dispositivo que se utiliza para almacenar energía eléctrica, generalmente en forma de celda química. Idealmente, presenta una tensión constante, variando su corriente de acuerdo a lo que impulse. En realidad, a medida que se utilice la batería, su voltaje comenzará a disminuir. Eventualmente, la energía almacenada en la batería se agotará y su voltaje caerá a cero. La capacidad de almacenamiento de una batería se mide en amperios-hora, Ah (o miliamperios-hora, mAh, para baterías más pequeñas). Siendo iguales todos los demás factores, la batería con la clasificación de amperios-hora más alta durará más tiempo antes de agotarse. Esto es cierto para el mismo tamaño de batería usando diferentes composiciones (por ejemplo, zinc-carbono versus alcalinas), así como baterías de diferentes tamaños físicos pero que tienen el mismo voltaje. Por ejemplo, todas las pilas AAA, AA, C y D tienen un voltaje nominal de 1.5 voltios. Si todos son del mismo tipo, como los alcalinos, entonces la diferencia práctica inmediata es que cuanto mayor sea el tamaño físico, mayor será su almacenamiento de energía y, por lo tanto, más durará.
En un rango modesto de corrientes, la vida útil esperada de una batería se puede calcular en función de su clasificación de amperios-hora y la corriente extraída de ella.
\[\text{Battery life } \approx \text{ amp-hour rating / current draw} \label{2.9} \]
Esta ecuación se usa mejor como una guía aproximada. Si el consumo de corriente es considerablemente mayor que la corriente a la que se probó la batería, la vida útil prevista será demasiado optimista. Por otro lado, si el consumo de corriente es considerablemente menor, es probable que la batería dure más de lo previsto.
La salida de corriente máxima de una batería es igualmente limitada. Si no fuera así, podríamos esperar que incluso baterías muy pequeñas produzcan corrientes fenomenalmente grandes durante periodos de tiempo muy cortos. Este no es el caso.
En la Figura {{template.index (ID:1)} se muestra un gráfico de curvas de descarga a diversas corrientes de carga. Observe cómo el voltaje de la batería comienza en los 1.5 voltios nominales y luego comienza a caer. Después de cierto punto, la tasa de disminución se acelera y “cae de un acantilado”. La vida útil real también dependerá de la aplicación, ya que algunos dispositivos pueden tolerar un voltaje más bajo que otros. Por ejemplo, una linterna anticuada seguirá funcionando con baterías en gran parte agotadas, simplemente no será tan brillante. Si tuviéramos que considerar el 75% de la tensión nominal como el límite inferior útil (un poco más de 1.1 voltios), vemos que a un consumo de 50 mA, la batería durará alrededor de 18 horas, logrando alrededor de 900 mAh. A 100 mA, durará alrededor de 7 horas, rindiendo 700 mAh. Si usáramos 1.0 voltios como nuestro límite inferior utilizable, llegaríamos a 1.05 Ah y 910 mAh, respectivamente.
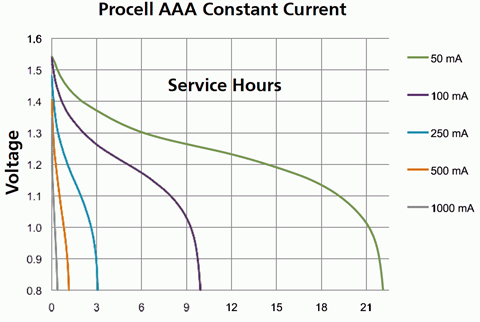
Figura 2.6.1 : Curvas de descarga de baterías para diversas corrientes de carga a temperatura ambiente. Cortesía de Duracell
Cierta batería tiene una clasificación de 10 Ah. Aproximadamente ¿cuánto tiempo durará con un consumo de 0.5 amperios?
\[Lifespan \approx \frac{Ah}{I} \nonumber \]
\[Lifespan \approx \frac{10 Ah}{500mA} \nonumber \]
\[Lifespan \approx 20 hours \nonumber \]
Recuerda, 20 horas es sólo una aproximación. Para una representación más precisa, considere el siguiente ejemplo.
Usando el gráfico de la Figura 2.6.1 , determine la vida útil esperada con un consumo de 100 miliamperios para un límite de voltaje inferior de 1.2 voltios. Determine también la calificación efectiva amp-hora en este punto.
La curva de 50 mA (púrpura) pasa a través de 1.2 voltios aproximadamente a las 5 horas. Esta es la vida útil esperada. La calificación correspondiente amp-hora es
\[Ah \approx I \times t \nonumber \]
\[Ah \approx 50mA \times 5 hours \nonumber \]
\[Ah \approx 250mAh \nonumber \]
Las baterías también tienden a mostrar un rendimiento disminuido con reducciones en la temperatura. Esto se muestra en la Figura 2.6.2 . Para esta batería en particular, la capacidad de congelación (0\(^{\circ}\) C) es aproximadamente la mitad de lo que es a temperatura ambiente (21\(^{\circ}\) C). La capacidad de corriente máxima también se puede reducir con la temperatura. Esto es cierto en muchos tipos de baterías, incluidas las grandes baterías automotrices de 12 voltios. Esta es una razón importante por la que los autos suelen ser mucho más difíciles de arrancar en días muy fríos; su capacidad actual se reduce, reduciendo así la salida del motor de arranque.
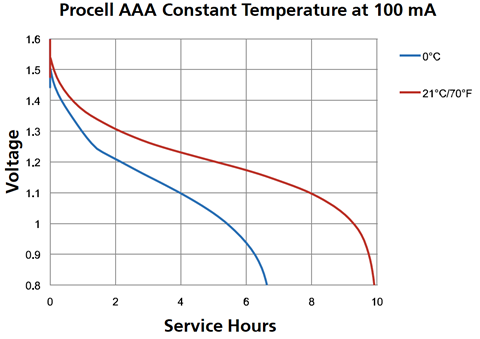
Figura 2.6.2 : Curvas de descarga de baterías para diferentes temperaturas. Cortesía de Duracell
En la Tabla {{template.index (ID:1)} se muestra una tabla de clasificaciones típicas de amperios-hora para tamaños de batería comunes. Estos valores son apropiados para baterías alcalinas de buena calidad. El NiMH recargable (hidruro de níquel-metal) sería aproximadamente el mismo. Recuerden, estas son solo aproximaciones.
| Tamaño de la batería | Capacidad (mAh) |
|---|---|
| AAA | 1000 |
| AA | 2500 |
| C | 5000 |
| D | 10000 |
| 9 Voltios | 500 |
Referencias
1 Recuerde, la potencia es la tasa de consumo de energía por unidad de tiempo, y así multiplicar la potencia por el tiempo produce energía. Un kWh es aproximadamente igual a 3.6 megajuulos.


