2.7: Resistencia y Conductancia

Hemos visto que tanto la corriente como la tensión tratan con el movimiento de carga. En consecuencia, en cualquier sistema eléctrico, el voltaje y la corriente están interrelacionados. Consideremos el caso más sencillo. Esto implicaría una sola fuente de voltaje, como una batería, accionando un solo elemento homogéneo como una longitud de cable o un bloque de un material dado. Las características físicas de este ítem dictarán cuánta corriente fluirá. En términos generales,

\[Effect = \frac{Cause}{Oppostion} \nonumber \]

En este caso la causa es la fuente de voltaje y el efecto es la corriente resultante. La oposición es la característica del ítem en cuestión, es decir, su capacidad para restringir el flujo de corriente. A esto le llamamos resistencia característica. En otras palabras, la resistencia es una medida de lo difícil que es establecer un flujo de corriente (es decir, “resistencia al flujo de corriente”) bajo un conjunto dado de circunstancias. Se denota por la letra\(R\) y tiene unidades de ohmios, en honor a Georg Ohm, investigador de principios del siglo XIX. La unidad se denota con la letra griega mayúscula omega,\( \Omega \).

A veces es más conveniente utilizar la visión inversa de este fenómeno, y en lugar de referirnos a lo difícil que es establecer una corriente, nos interesaría lo fácil que es establecer una corriente. Esto se llama conductancia y es el recíproco de la resistencia. La conductancia se denota por la letra\(G\) y tiene unidades de siemens, que llevan el nombre de Werner von Siemens. La unidad se abrevia como S.

\[R = \frac{1}{G} \\ G = \frac{1}{R} \label{2.10} \]

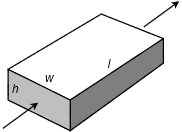
Figura 2.7.1 : Definición de resistencia.

En este sencillo escenario, la resistencia es una función del material por el que pasa la corriente junto con su forma. Esto se ilustra en la Figura 2.7.1 donde la flecha muestra la dirección del flujo de corriente. Una pregunta obvia es “¿De qué está hecho este bloque?” No debería sorprender que el material elegido tenga un gran impacto en la corriente. Ya hemos visto que los metales como el cobre son buenos conductores de la electricidad. Otros materiales, como ciertos plásticos y cerámicas, no lo son. Estos materiales se denominan aislantes.

La medida de la capacidad inherente y general de un material para restringir el flujo de corriente se llama resistividad. La resistividad se denota con la letra griega\(\rho\) (rho). Siendo iguales todos los demás factores, cuanto mayor sea la resistividad, mayor será la resistencia. Además, cuanto mayor sea la longitud del material por el que debe pasar la corriente, mayor es la resistencia. Finalmente, a medida que crece el área superficial de la sección transversal (es decir, la cara), la resistencia disminuye. Expresado como una fórmula

\[R = \frac{\rho l}{A} \label{2.11} \]

Dónde

\(R\)es la resistencia en ohmios,

\(\rho\)es la resistividad,

\(l\)es la longitud del material,

\(A\)es el área de la cara (\(h\)veces\(w\)).

La resistividad a menudo se especifica en ohmios-centímetros con la longitud y el área especificados de manera similar en centímetros y centímetros cuadrados, respectivamente. Una tabla de valores de resistividad para una variedad de materiales se muestra en la Tabla 2.7.1 . Tenga en cuenta que la resistividad no es necesariamente constante a través de la temperatura. En efecto, este cambio puede ser aprovechado como un medio para medir la temperatura. En otras aplicaciones, podríamos necesitar que sea lo más estable posible a través de la temperatura. Esta necesidad condujo a la creación de las aleaciones Constantan y Manganina a finales del siglo XIX que exhiben una estabilidad muy alta a través de la temperatura.

De esta tabla podemos ver que la plata tiene menor resistividad que el cobre que a su vez es menor que el oro. Esto significa que si fabricamos alambres de tamaño idéntico de estos tres materiales, la versión plateada tendría la menor resistencia y el oro el más alto. ¿Por qué entonces, los cables de audio y video suelen tener chapado en oro? Ciertamente, no se debe a una menor resistividad y mayor conductividad. La razón es que el oro es un metal noble, es decir, que no se empaña. En contraste, la superficie tanto de plata como de cobre se oxidará, creando una pátina (la “mancha” oscura que se nota en los implementos de plata vieja y cobre). El óxido creará una capa de alta resistencia y reducirá la integridad de la conexión.

Es importante señalar que la Fórmula\ ref {2.11} no incluye un término para la masa del material. Sólo se refiere a la forma del artículo. Esta es una distinción importante. Si alteráramos la masa pero mantuviéramos igual la relación entre la longitud y el área, la resistencia resultante no cambiaría. En general, el aumento de masa por sí mismo no necesariamente altera la resistencia pero puede tener un impacto en la capacidad de manejo de potencia del dispositivo.

Tabla 2.7.1 : Valores de resistividad para diversos materiales.

Material	Resistividad\(\rho (\Omega \cdot \) cm) a 20\(^{\circ}\) C	Coeficiente de temperatura (K\(^{−1}\))
Plata	1.59\(\times 10^{−6}\)	0.0038
Cobre	1.68\(\times 10^{−6}\)	0.00404
Oro	2.44\(\times 10^{−6}\)	0.0034
Aluminio	2.65\(\times 10^{−6}\)	0.0039
Zinc	5.90\(\times 10^{−6}\)	0.0037
Níquel	6.99\(\times 10^{−6}\)	0.006
Hierro	9.7\(\times 10^{−6}\)	0.005
Platino	1.06\(\times 10^{−5}\)	0.00392
Estaño	1.09\(\times 10^{−5}\)	0.0045
Titanio	4.20\(\times 10^{−5}\)	0.0038
Manganina	4.82\(\times 10^{−5}\)	0.000002
Constantan	4.90\(\times 10^{−5}\)	0.000008
Acero inoxidable	6.90\(\times 10^{−5}\)	0.00094
Nichrome	1.10\(\times 10^{−4}\)	0.0004
Carbono (amorfo)	5\(\times 10^{−4}\) a 8\(\times 10^{−3}\)	−0.0005
Silicio	6.4\(\times 10^{4}\)	−0.075
Vidrio	1\(\times 10^{13}\) a 1\(\times 10^{17}\)
Carbono (diamante)	1\(\times 10^{14}\)
Caucho duro	1\(\times 10^{15}\)
Aire	\(10^{11}\)a\(10^{17}\)
MASCOTA	1\(\times 10^{23}\)
Teflón	1\(\times 10^{25}\) a 1\(\times 10^{27}\)

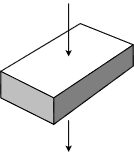
Figura 2.7.2 : La resistencia cambiará debido a la alteración del área y la longitud con la masa sin cambios.

Por el contrario, si tomamos esa masa original y la reformamos, o simplemente aplicamos la corriente a una cara de diferencia, de tal manera que el área de superficie efectiva y la longitud cambian, entonces la resistencia resultante también cambiará. Esto se ilustra en la Figura 2.7.2 . Aquí hemos tomado el ítem que se muestra en la Figura 2.7.1 y hemos dirigido el flujo de corriente de arriba a abajo en lugar de a través del lado. En esta orientación, la superficie se incrementa mucho y se reduce considerablemente la longitud a través de la cual debe recorrer la corriente. En consecuencia, la resistencia efectiva en esta orientación será considerablemente menor que la vista en el original.

Ejemplo 2.7.1

Un determinado material tiene una resistividad de 0.2 ohm-centímetros. Determinar la resistencia de una pieza que tenga 0.3 cm de ancho, 0.5 cm de alto y 4 cm de largo.

\[A = h \times w \nonumber \]

\[A = 0.5cm \times 0.3cm \nonumber \]

\[A = 0.15 cm^2 \nonumber \]

\[R = \frac{ \rho l}{A} \nonumber \]

\[R = \frac{0.2 \Omega cm \times 4cm}{0.15cm^2} \nonumber \]

\[R = 5.333 \Omega \nonumber \]

Para nuestro siguiente ejemplo, consideremos un carrete de alambre. En muchos casos tratamos el alambre de manera ideal, como si no tuviera resistencia. Si bien esto puede ser una buena aproximación en muchos casos, especialmente con tramos de alambre relativamente cortos, tal no siempre es el caso.

Ejemplo 2.7.2

Un cierto calibre de alambre de cobre tiene un diámetro de 0.6 mm. Determine la resistencia si el carrete tiene 200 metros de largo.

El cuadro 2.7.1 indica que la resistividad del cobre es de 1.68E−6 ohm-centímetros. El truco aquí es que debemos mantener las unidades consistentes. Como hay 100 centímetros al metro, la longitud es de 200 metros por 100, o 20,000 centímetros (es decir, 20E3). Dado que hay 10 milímetros al centímetro, el diámetro debe disminuirse en un factor de diez, produciendo un diámetro de 0.06 cm y con ello un radio de 0.03 cm.

\[A = \pi r^2 \nonumber \]

\[A = \pi (0.03cm)^2 \nonumber \]

\[A = 2.83E-3cm^2 \nonumber \]

\[R = \frac{ \rho l}{A} \nonumber \]

\[R = \frac{1.68E-6 \Omega cm \times 20E3 cm}{2.83E-3cm^2} \nonumber \]

\[R = 11.9 \Omega \nonumber \]

La cantidad de resistencia que se ve en el Ejemplo 2.7.2 se consideraría excesiva si el elemento a conectar es algo tan simple como un altavoz, que normalmente estaría alrededor de 8\( \Omega \). Y aunque probablemente nadie necesitaría 200 metros de cable para conectar un altavoz en su casa, ese tipo de distancia no sería nada destacable en un estadio grande o terminal del aeropuerto. No lo olvides, necesitaríamos cables hacia y desde el altavoz, logrando una separación total de 100 metros como máximo.

Varios grosores de cables y alambres se utilizan para una amplia variedad de propósitos. Para que esto sea más fácil, se han estandarizado los espesores de alambre. El estándar más común en América del Norte es el Calibre de Alambre Americano, o AWG. Se trata de una especificación no métrica con orígenes a mediados del siglo XIX. Cuanto mayor sea el número de calibre, menor será el diámetro del cable y menor será la corriente que puede transportar de manera segura. Para poner los números de calibre en perspectiva, los electrodomésticos pequeños típicos usan cables de calibre 16 o 18, el cableado doméstico básico usa calibre 12 (con un disyuntor de 20 amperios) y el cable de conexión utilizado en una placa de pruebas sin soldadura de laboratorio de circuitos eléctricos o electrónica es comúnmente de calibre 22 o 24.

Para el cableado de uso general, el cobre es, con mucho, el metal más común utilizado porque es altamente conductor y relativamente económico. Algunos otros metales se utilizan en casos especiales, por ejemplo, el aluminio se utiliza para líneas de transmisión de energía de larga distancia.

Tabla 2.7.2 : Datos de cable AWG para conductores de cobre.

AWG	Diámetro (pulg)	Diámetro (mm)	Resistencia/longitud (\(\Omega\)/km)	Resistencia/longitud (\(\Omega\)/1000ft)
0000 (4/0)	0.4600	11.684	0.1608	0.04901
00 (2/0)	0.3648	9.266	0.2557	0.07793
0 (1/0)	0.3249	8.251	0.3224	0.09827
2	0.2576	6.544	0.5127	0.1563
4	0.2043	5.189	0.8152	0.2485
6	0.1620	4.115	1.296	0.3951
8	0.1285	3.264	2.061	0.6282
10	0.1019	2.588	3.277	0.9989
12	0.0808	2.053	5.211	1.588
14	0.0641	1.628	8.286	2.525
16	0.0508	1.291	13.17	4.016
18	0.0403	1.024	20.95	6.385
20	0.0320	0.812	33.31	10.15
22	0.0253	0.644 5	52.96	16.14
24	0.0201	0.511	84.22	25.67
26	0.0159	0.405	133.9	40.81
32	0.00795	0.202	538.3	164.1
40	0.00314	0.0799	3441	1049

Una tabla de tamaños de calibre y parámetros asociados se muestra en la Tabla 2.7.2 . Esta tabla asume que se está utilizando cobre para el cable. Tenga en cuenta que a medida que disminuye el diámetro del alambre, la cantidad de resistencia para una longitud particular aumenta, como se esperaba de la Ecuación\ ref {2.11}.

Usando esta tabla podemos realizar una comprobación cruzada rápida del Ejemplo 2.7.2 . El diámetro de alambre utilizado en ese ejemplo fue de 0.6 mm que es un poco más pequeño que AWG 22 como se indica en la tabla. Además, se indica que el cable #22 tiene una resistencia de aproximadamente 53\( \Omega \) por km. Para 200 metros, como se usa en el problema del ejemplo, esto funciona a 10.6\( \Omega \). Como el alambre #22 es ligeramente mayor en diámetro, esperamos que muestre una resistencia ligeramente menor que el valor calculado de 11.9\( \Omega \), lo que hace.

Si bien puede no ser inmediatamente aparente, los números de calibre proceden de una manera logarítmica basada en el diámetro. Al aumentar un número de calibre (por ejemplo, de #10 a #11) se disminuye el diámetro en un factor de aproximadamente 0.89. Como la resistencia es inversamente proporcional al cuadrado del diámetro (es decir, el área), la resistencia aumenta en más de 25%. Los tamaños numerados pares son particularmente comunes en uso y un salto al siguiente número de calibre par más alto (por ejemplo, #18 a #20) produce un aumento de resistencia de casi 60%.

Resistencias y el código de color de la resistencia

Las resistencias son dispositivos utilizados para controlar las corrientes y tensiones en un circuito. Están disponibles en muchas formas y tamaños, y normalmente están diseñados para mantener valores óhmicos estables a pesar de los cambios ambientales como la temperatura y la humedad. Una muestra de diferentes estilos de resistencia se muestra en la Figura 2.7.3 . Como regla general, cuanto mayor sea la resistencia, mayor será la potencia que puede manejar. En la parte posterior de la figura hay una gran resistencia de potencia cerámica que utiliza una carcasa rectangular de aluminio. Este dispositivo está clasificado para 200 vatios de disipación. Inmediatamente delante y a la derecha de ella hay varias resistencias de potencia de cerámica más pequeñas con clasificaciones en el rango de 5 a 20 vatios. A lo largo del lado izquierdo hay un conjunto de resistencias de película de carbono y composición de carbono que van desde 1 vatio hasta una décima vatio en disipación. Hacia el centro hay una resistencia de chip de múltiples conductores que contiene varias resistencias en un paquete. Con pocas excepciones, todos estos artículos se clasifican como componentes de “orificio pasante”, es decir, sus cables están diseñados para pasar por agujeros pretaladrados en una placa de circuito impreso. Estos son también los componentes más utilizados en un laboratorio eléctrico, ya que los cables encajan en placas de prueba sin soldadura y los componentes son de un tamaño conveniente.

Figura 2.7.3 : Una variedad de resistencias diferentes.

Con el creciente deseo de encoger componentes, los diseños de producción modernos utilizan técnicas de montaje en superficie en lugar de la construcción de orificios pasantes. En la parte inferior central hay un punto pequeño que es, de hecho, una resistencia de montaje en superficie capaz de 1/2 vatio de disipación de potencia. Un primer plano se muestra en la Figura 2.7.4 . Obviamente, estos dispositivos son demasiado pequeños para ser prácticos de usar sin equipo especial.

Figura 2.7.4 : Cierre de una resistencia de montaje en superficie.

Las resistencias son dispositivos bilaterales lineales. Al ser lineales, su relación corriente-voltaje se puede dibujar como una línea recta. Bilateral significa que la polaridad del voltaje o la dirección de la corriente no importará. En otras palabras, a diferencia de una batería, estos dispositivos no pueden insertarse en un circuito hacia atrás porque cualquiera de las dos orientaciones funciona de la misma manera. Si el eje horizontal es voltaje y el vertical es corriente, entonces la pendiente de la línea produce la conductancia. Así, cuanto más pronunciada es la línea, menor es su resistencia. Esto se ilustra en la Figura 2.7.5 .

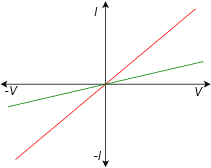
Figura 2.7.5 : Gráfica corriente-voltaje de dos resistencias.

No todos los componentes eléctricos son lineales y bilaterales. Un buen ejemplo es el diodo semiconductor, un dispositivo de uso común en sistemas electrónicos. El gráfico de corriente-voltaje de un diodo se muestra en la Figura 2.7.6 para comparación. Tenga en cuenta que la trama no es una simple línea recta, por lo tanto no es lineal. Además, las respuestas del primer y tercer cuadrante son tremendamente diferentes, lo que indica que la polaridad es de suma importancia. Claramente, importa de qué manera se insertan este tipo de dispositivos en un circuito.

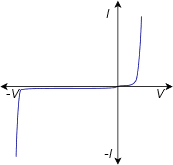
Figura 2.7.6 : Gráfica corriente-voltaje de un diodo: ni lineal ni bilateral.

Las resistencias están disponibles en valores óhmicos estandarizados y en clasificaciones de potencia estandarizadas (ver Apéndice A). Junto con su valor de resistencia, las resistencias también tienen una tolerancia especificada. Esto especifica un rango permisible de variación del valor declarado. Por ejemplo, una resistencia de 220 ohmios puede tener una tolerancia del 10%. Esto significa que el valor real de cualquier espécimen dado de una caja de estas resistencias puede estar fuera de la placa de identificación o valor nominal en 10% o 22 ohmios. Por lo tanto, cualquier resistencia en particular podría ser tan alta como 242 ohmios o tan baja como 198 ohmios.

Las resistencias de propósito general utilizan un código de color para denotar su valor y tolerancia. Normalmente, esto implicará cuatro franjas de color: dos para la precisión/mantisa, una para la potencia de diez, y la cuarta para indicar la tolerancia. Para mayor precisión, se puede usar una versión de cinco bandas con las tres primeras denotando la precisión/ mantisa. Como alternativa, las resistencias de alta precisión pueden tener su valor nominal impreso directamente sobre ellas. Consulte la Figura 2.7.7 para ver un ejemplo de la variedad básica.

Figura 2.7.7 : Ejemplo de código de color básico de resistencia de cuatro bandas.

Las dos primeras bandas, aquí amarillo y violeta, indican la precisión o los dígitos iniciales. La tercera banda, aquí naranja, indica la potencia de diez o “número de ceros” a sumar. La cuarta banda, plateada en este ejemplo, indica la tolerancia. Tenga en cuenta que la cuarta banda está espaciada de las demás para evitar revertir accidentalmente el orden.

El código de color se muestra en la Figura 2.7.8 . Para ayudar a recordar la secuencia, se han utilizado varias ayudas mnemotécnicas, comenzando la primera letra de cada palabra con la misma letra que el color correspondiente. Un ejemplo es el “Picnic Basket Mnemonic” que es: Osos Negros Robaron Nuestras Deliciosas Golosinas Golpeando a Varios Lobos Grises. Otra posibilidad es señalar que la sección media sigue un arcoíris con blanco y negro en los extremos extremos.

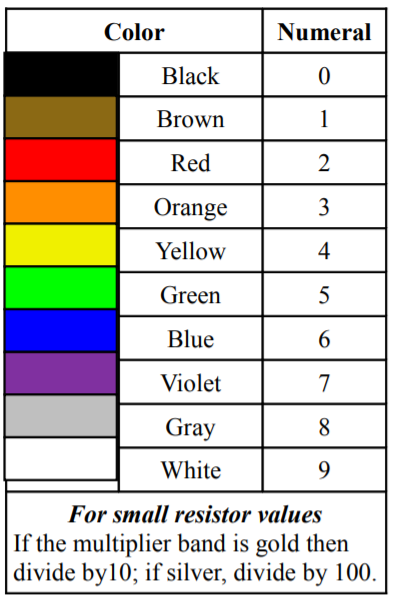
Figura 2.7.8 : Código de color de resistencia.

Los colores de la banda de tolerancia son los siguientes: Para las partes básicas la plata es\(\pm\) del 10% y el oro es\(\pm\) del 5%. Si se omite la cuarta banda, esto indica una tolerancia del\(\pm\) 20%, aunque rara vez se usa en diseños modernos. Para piezas de precisión se reutilizan algunos colores pero siguen los números del código de color: El marrón es\(\pm\) 1% de tolerancia y el rojo es\(\pm\) 2% de tolerancia. Tolerancias más ajustadas también están disponibles. A veces se agrega una banda extra que indica un índice de confiabilidad o coeficiente de temperatura. En tales casos, lo mejor es consultar las hojas de datos del fabricante para obtener detalles. No vamos a seguir adelante con estos.

Ejemplo 2.7.3

Determine los valores nominales, máximos y mínimos de resistencia aceptables para la resistencia que se muestra en la Figura 2.7.2 .

Los colores son amarillo-violeta-naranja. Esto se traduce en 4, 7 y 3. El valor es “47 con 3 ceros”, o 47000 ohmios. La cuarta banda plateada indica 10% de tolerancia. Así, la resistencia en la foto es nominalmente 47 k\( \Omega \) con\(\pm\) 10% de variación alrededor del valor nominal siendo aceptable. La tolerancia rinde\(\pm\) 4.7 k\( \Omega \), por lo que el rango aceptable es de 42.3 k\( \Omega \) a 51.7 k\( \Omega \).

Ejemplo 2.7.4

Una resistencia de precisión tiene un código de color naranja-azul-verde-marrón-marrón. Determinar su valor y rango aceptable.

La banda final indica que se trata de un componente de tolerancia\(\pm\) del 1%. Los primeros cuatro colores se traducen a 3, 6, 5 y 1. El valor es “365 con 1 cero”, y así 3650 ohmios, o 3.65 k\( \Omega \). El rango permitido es de 3.65 k\( \Omega \)\(\pm\) 36.5\( \Omega \).

Ejemplo 2.7.5

Determinar el valor nominal y la tolerancia de una resistencia con el código de color verde-azul-oro-plata.

Los dos primeros colores se traducen a 5 y 6. Oro en la tercera banda significa “multiplicar por 0.1”. La banda final indica que se trata de un componente de tolerancia del\(\pm\) 10%. Por lo tanto, el valor nominal es 5.6\( \Omega \). El rango permitido es 5.6\( \Omega \)\(\pm\) 0.56\( \Omega \).

Un ejemplo de una hoja de datos de resistencia se muestra en la Figura 2.7.9 . Esta hoja de datos es para una serie de resistencias de chip de montaje en superficie. Los grados de tolerancia disponibles varían de 0.5% a 20%. Además, para cada variante hay dos coeficientes de temperatura disponibles siendo el más estable 100 ppm/\(^{\circ}\) C (ppm es corto para “partes por millón”, así 100 ppm equivale a 0.01%). Tenga en cuenta que estos dispositivos son demasiado pequeños para usar el código de color de la resistencia. En cambio, se imprime directamente sobre ellos un código numérico que sigue las reglas para las bandas de color, lo que significa que el dígito final es el multiplicador. Así, “150” es 15\( \Omega \) (1-5 sin ceros). La excepción son valores muy pequeños donde se usa la letra “R” en lugar de un punto decimal. En consecuencia, “2R4” es 2.4\( \Omega \).

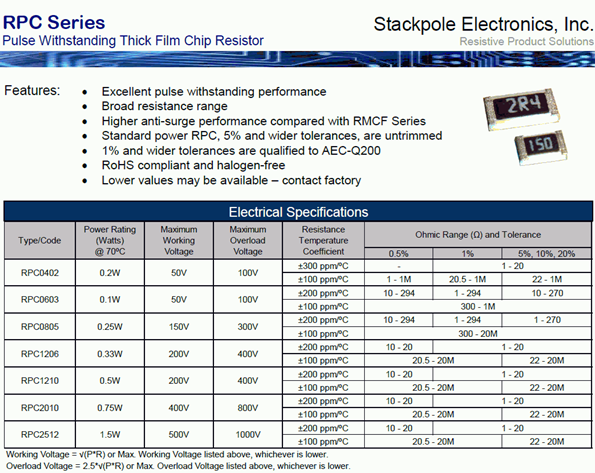
Figura 2.7.9 : Hoja de datos de ejemplo de resistencia. Cortesía de Stackpole Electronics

Una característica particularmente importante de la mayoría de los dispositivos electrónicos es su capacidad de manejo de energía. Para esta serie hay varias variaciones con manejo de potencia de 0.1 watts a 1.5 watts, y voltajes de trabajo máximos de hasta 500 voltios. El manejo de energía también es una función de la temperatura ambiente. En general, los dispositivos tienen una temperatura interna máxima que pueden alcanzar antes de que se dañen. El control del calor tiende a ser un problema importante en muchos diseños de sistemas. Si la temperatura ambiente aumenta, hay menos “espacio libre” para el aumento de temperatura del dispositivo y, por lo tanto, el dispositivo no podrá disipar tanta energía. Esto se ilustra en la gráfica de la Figura 2.7.10 .

Observe cómo la disipación de potencia es constante a temperaturas de 70\(^{\circ}\) C. Esta temperatura se considera la temperatura máxima de funcionamiento normal para este dispositivo y la disipación de potencia a esta temperatura es la citada en la hoja de datos. Si el dispositivo se opera en un ambiente más cálido, la disipación de potencia se reduce en el porcentaje dado en la gráfica. Por ejemplo, a 100\(^{\circ}\) C la disipación es solo alrededor del 65% de la calificación nominal. De particular importancia, a 155\(^{\circ}\) C el dispositivo ya no puede disipar ninguna potencia, y por lo tanto esta temperatura sirve como techo absoluto. Después de todo, una resistencia que no puede disipar ninguna potencia es una resistencia que no puede tener ninguna corriente a través de ella o voltaje a través de ella sin quemarse. Es esencialmente no funcional.

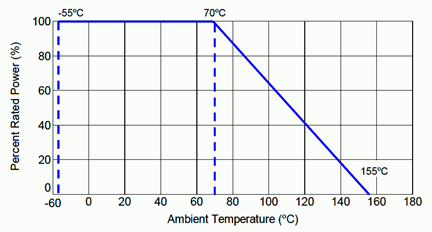
Figura 2.7.10 : Gráfico de reducción de potencia de resistencia. Cortesía de Stackpole Electronics

Por supuesto, al igual que una sartén en una estufa, estos dispositivos no se calientan instantáneamente, es decir, exhiben una constante de tiempo térmico. Tardan cierta cantidad de tiempo en calentarse (y también en enfriarse). Por períodos cortos, los dispositivos pueden manejar considerablemente más potencia que su clasificación a largo plazo. El gráfico de la Figura 2.7.11 , muestra la disipación de potencia para pulsos individuales. En algunos casos, estas resistencias pueden manejar potencias de un orden de magnitud mayor. Por ejemplo, considere el tipo RPC0402 (línea inferior). De la hoja de datos de la Figura 2.7.9 se especifica que este dispositivo tiene una clasificación a largo plazo de 0.2 vatios. En contraste, la gráfica de la Figura 2.7.11 muestra que es capaz de soportar un solo pulso mayor a 20 vatios por 100 microsegundos, poco menos de 10 vatios para un pulso de milisegundos y aproximadamente 2 vatios para un pulso de una décima de segundo.

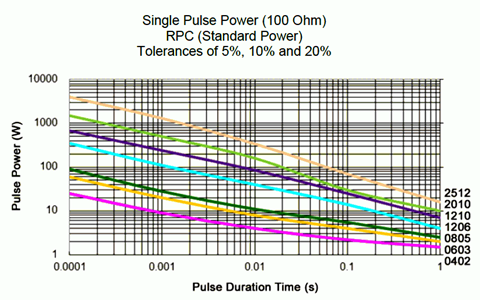
Figura 2.7.11 : Disipación de potencia de pulso. Cortesía de Stackpole Electronics

Otros dispositivos resistivos

Junto con las resistencias fijas estándar, existen varios otros tipos de dispositivos resistivos que han sido diseñados para ser sensibles a los cambios en su entorno. Así, pueden servir como sensores ya que a medida que cambia su resistencia, impacta el flujo de corriente y el voltaje resultante. Veremos ejemplos de esto en los próximos trabajos. Algunos de los insumos ambientales incluyen temperatura, fuerza y niveles de luz.

Resistencia de detección de fuerza (FSR)

La resistencia de detección de fuerza consta de dos capas de material con una distancia de separación nominal. Se presenta como una membrana plana que suele ser redonda o rectangular, y quizás con un respaldo adhesivo. Un ejemplo de una FSR se muestra en la Figura 2.7.12 . Sin aplicar fuerza, el dispositivo muestra una resistencia extremadamente alta, bien en los megohmios. A medida que se aplica fuerza a la superficie, las dos capas entran en mejor contacto lo que disminuye la resistencia neta. Esto se constata en la gráfica de la Figura 2.7.13 . El gráfico muestra aproximadamente una respuesta de línea recta entre resistencia y fuerza cuando se representa en una escala logarítmica y logarítmica. En los niveles de fuerza más altos, la resistencia puede caer a solo unos cientos de ohmios.

Figura 2.7.12 : Una resistencia de detección de fuerza (FSR).

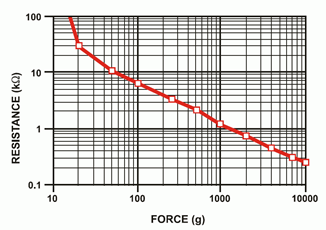
Figura 2.7.13 : Curva de respuesta de FSR. Cortesía de Interlink Electronics

Fotorresistor

Como su nombre lo indica, las fotorresistencias son sensibles a los cambios en el nivel de luz. También se les llama LDR, abreviatura de Resistor Dependiente de Luz. Se pueden usar diferentes materiales en su construcción, pero el más común es el sulfuro de cadmio, CdS. Como consecuencia, las fotorresistencias a veces se denominan genéricamente “células CDs”.

Una fotorresistencia se muestra en la Figura 2.7.14 junto con su correspondiente gráfica de resistencia en la Figura 2.7.15 . En total oscuridad el dispositivo exhibe una resistencia muy alta. A medida que aumentan los niveles de luz, la resistencia disminuye. Al igual que con la FSR, vemos una relación inversa entre la resistencia y el factor ambiental: a medida que aumenta el aporte ambiental (fuerza, nivel de luz), la resistencia hace lo contrario y disminuye. Y una vez más, vemos una línea recta cuando se traza con escalas log-log. Técnicamente, nos referimos a esto como una relación negativa porque la pendiente de la línea de la trama es negativa.

Figura 2.7.14 : Un fotoresitor, o LDR.

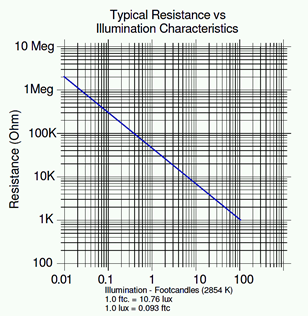
Figura 2.7.15 : Curva de respuesta del fotoresitor. Cortesía de Advanced Photonix

Para poner el brillo de la luz en términos comunes, 0.01 velas de pie (aproximadamente 0.1 lux) equivale a una noche clara iluminada por la Luna. En este nivel, la fotorresistencia está mostrando más de 1 megaohm de resistencia. En contraste, velas de 100 pies (aproximadamente 1000 lux) equivale a un día nublado (como referencia, la luz solar directa es quizás 100 veces más fuerte). En este nivel, el valor de la fotorresistencia ha bajado a unos 1000 ohmios.

Un punto digno de mención es que la luz que la fotorresistencia “ve” no es necesariamente la misma que la que ve un humano. La sensibilidad del dispositivo a varias longitudes de onda (es decir, colores) puede diferir marcadamente de la visión humana. De hecho, diferentes materiales exhiben diferentes sensibilidades a diversas longitudes de onda. Algunas de estas pueden ser longitudes de onda que el ojo humano sin ayuda no puede ver en absoluto (infrarrojo o ultravioleta, por ejemplo).

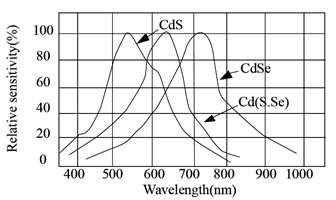
Figura 2.7.16 : Curvas de sensibilidad del fotorresitor. Cortesía de Token Electronics

Un ejemplo de curvas de sensibilidad se muestra en la Figura 2.7.16 . Observe las variaciones entre los diferentes materiales, siendo los CD uno de los tres (lado izquierdo). Las sensibilidades máximas varían al igual que las formas precisas. En la práctica, esto significa que algunas de estas unidades serán más o menos sensibles a ciertos colores que otras unidades. La curva de CdS indica una sensibilidad máxima de aproximadamente 540 nm, la cual corresponde al verde. En comparación, la celda de CdSe (seleniuro de cadmio) exhibe un pico de poco más de 700 nm, lo que corresponde a rojo. En algunas longitudes de onda, la respuesta relativa de un material puede ser no más del 10% de la respuesta de un material diferente.

Es importante señalar que el uso de cadmio, como en celdas de CD y similares, está severamente restringido por la directiva RoHS (ver Capítulo Uno).

Termistor

Un termistor es un dispositivo cuya resistencia es una función de la temperatura. Estos dispositivos están disponibles en dos tipos básicos. Ya sea PTC, para Coeficiente de Temperatura Positivo; o NTC, para Coeficiente de Temperatura Negativo. Los dispositivos PTC muestran un aumento en la resistencia a medida que aumenta la temperatura y los dispositivos NTC muestran una disminución en la resistencia a medida que aumentan las temperaturas. Idealmente, estas son relaciones lineales con las gráficas que muestran líneas rectas. La realidad es que la linealidad solo puede asumirse a través de rangos de temperatura bastante estrechos. Para rangos más amplios, habrá una desviación notable de una línea recta ya que la curva es de naturaleza logarítmica. Un termistor NTC básico se muestra en la Figura 2.7.17 .

Figura 2.7.17 : Termistor NTC.

Los gráficos genéricos de rendimiento del termistor se muestran en la Figura 2.7.17 con la respuesta de línea recta idealizada en la parte superior y la respuesta no lineal más realista a continuación. Los termistores se especificarán en términos de su resistencia a temperatura ambiente (generalmente se toma como 25\(^{\circ}\) C) junto con su sensibilidad que se denota como beta (\(\beta\)). Cuanto mayor sea el valor de beta, más pronunciada es la curva y mayor es la sensibilidad. Las curvas etiquetadas como Beta 2 muestran mayor sensibilidad, lo que significa que habrá un mayor cambio en la resistencia para un cierto cambio de temperatura.

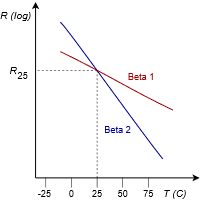
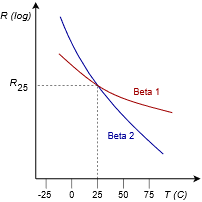
Figura 2.7.18 : Curvas de respuesta del termistor NTC: Ideal (arriba) y real.

La siguiente ecuación puede ser utilizada para determinar la resistencia de un termistor a alguna otra temperatura de interés con mayor precisión que usando una simple aproximación lineal. Todo lo que se necesita es una temperatura de referencia y resistencia correspondiente, el valor beta y la nueva temperatura de interés. Usando una temperatura de referencia de 25\(^{\circ}\) C:

\[R_T = R_{25} e^{\beta \left( \frac{1}{T} − \frac{1}{298.15} \right)} \label{2.12} \]

Dónde

\(R_T\)es la resistencia a la nueva temperatura Kelvin\(T\),

\(R_{25}\)es la resistencia a 25\(^{\circ}\) C,

\(T\)es la temperatura de interés en kelvin,

\(\beta\)es la versión beta del dispositivo.

Obsérvese que la constante “298.15” en la Ecuación\ ref {2.12} es equivalente a la temperatura de referencia de 25\(^{\circ}\) C (0 K es −273.15\(^{\circ}\) C). En consecuencia, si se utiliza un punto de referencia diferente, simplemente inserte la nueva temperatura de referencia en su lugar y use la resistencia correspondiente en lugar de\(R_{25}\).

Varistor

Los varistores se utilizan como dispositivos limitadores, principalmente para suprimir picos de voltaje no deseados en equipos electrónicos. El varistor es un dispositivo único en el sentido de que tiene una característica de corriente-voltaje altamente no lineal. Esto se muestra en la Figura 2.7.19 . Recuerde, cuando se traza con el voltaje en el eje horizontal, la pendiente de la línea representa la conductancia. En consecuencia, el varistor muestra una región de conductancia cercana a cero o resistencia extremadamente alta (la sección horizontal), y dos secciones que son casi verticales, lo que indica conductancia extremadamente alta o resistencia cercana a cero. Esta característica permite que el varistor actúe como un dispositivo limitador.

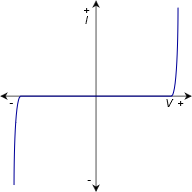
Figura 2.7.19 : Característica de corriente-voltaje de un varistor

Imagínese que un rayo afecta a una línea eléctrica local. Esto creará un pico repentino pero de corta duración en el voltaje. Una salida de pared normal de 120 voltios normalmente produce picos regulares de aproximadamente 170 voltios. Un rayo podría agregar varios cientos de voltios a esto. El voltaje resultante podría ser tan alto que dañaría los equipos electrónicos conectados a la toma de corriente. Para aliviar este problema, se puede colocar un varistor a través de las líneas de voltaje de entrada. Los voltajes del punto de ruptura vertical se establecerían para un valor poco más de 170 voltios, el máximo normal. En circunstancias típicas el varistor vería una tensión en su región horizontal y así se comportaría como una resistencia muy alta. Prácticamente no drenaría corriente de la salida, y en consecuencia no tendría ningún impacto en el resto de los circuitos. Por otro lado, si un pico grande golpea la línea, el varistor oscilará hacia la región vertical, mostrará una resistencia muy reducida y actuará como un camino de derivación para la corriente del pico. Fijará efectivamente el voltaje a algún valor nominal máximo. Por supuesto, el varistor tiene que absorber la energía que presenta ese pico, y los parámetros importantes de un varistor incluyen la cantidad de energía que puede absorber (en julios) y su capacidad máxima de corriente, junto con el voltaje máximo de sujeción.

Calibrador extensométrico

La galga extensiométrica es un dispositivo utilizado para medir la tensión mecánica en algún artículo. La tensión ocurre cuando un artículo está bajo compresión (su longitud se acorta o se reduce) o cuando está bajo tensión (se alarga o estira). Ambas cosas pueden suceder simultáneamente, por ejemplo cuando una barra está experimentando flexión o par (un lado está bajo compresión mientras que el otro está bajo tensión). La deformación de ingeniería se define como el cambio en la longitud sobre la longitud inicial. Si un artículo experimenta demasiada tensión, puede deformarse permanentemente o fallar (por ejemplo, el tren de aterrizaje en una aeronave o los componentes de la suspensión en un automóvil). En pocas palabras, se utilizan galgas extensométricas para medir este efecto.

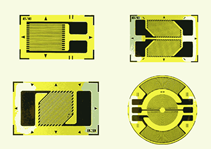
Figura 2.7.20 : Calibres de deformación. Cortesía de Zemic

Una galga extensiométrica está hecha típicamente de lámina metálica muy delgada en un patrón específico. Consulte la Figura 2.7.20 para ver ejemplos de formas. Por lo general, la forma es la de una serie de líneas finas conectadas en un patrón de ida y vuelta, los dos extremos terminan en almohadillas más grandes para soldar en cables de conexión. En funcionamiento, la galga extensiométrica se pega al material que se investiga, por ejemplo, una barra metálica que forma parte de un sistema de suspensión. A medida que se pegan entre sí, la galga extensiométrica experimenta la misma deformación que la barra de metal. Cualquier deformación creará cambios en la longitud de los alambres de lámina de la galga extensiométrica, así como en su área de superficie frontal. Por ejemplo, bajo tensión, la longitud aumenta mientras que el área superficial disminuye (el área de superficie debe disminuir porque el alambre de aluminio tiene masa finita). Recordando la relación básica de resistencia, Ecuación\ ref {2.11}, ambos efectos harán que la resistencia suba. Cuanto mayor sea la tensión bajo tensión, mayor será el aumento de la resistencia. Lo contrario ocurrirá bajo compresión y la resistencia disminuirá. Estos cambios en la resistencia no son grandes pero son suficientes para alterar la tensión o corriente asociada que luego se puede calibrar para determinar la tensión aplicada.