2.10: Ejercicios

Última actualización
Guardar como PDF

Page ID: 86061

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Análisis

1. Un multímetro digital de 2000 cuentas tiene una especificación de precisión de$\pm$ 1%. Si lee un voltaje de 34.2 voltios, ¿cuál es el rango posible del voltaje verdadero?

Respuesta 1

33.858V a 34.542V

2. Un multímetro digital de 4000 cuentas tiene una especificación de precisión de$\pm$ 0.5%. Si lee una corriente de 142.0 mA, ¿cuál es el rango posible de la corriente verdadera?

3. Determinar las escalas de voltaje esperadas para un medidor de dígitos estándar de “tres y medio” entre 1 y 1000 voltios.

Respuesta 3

Básculas de 2 Volt, 20Volt y 200 Volt

4. Determinar las escalas de corriente esperadas para un medidor de dígitos estándar de “tres y medio” entre 1 mA y 1 amperio.

5. Un multímetro digital de 2000 cuentas tiene una especificación de precisión de$\pm$ 2% y$\pm$ 5 recuentos. Si lee un voltaje de 7.00 voltios, ¿cuál es el rango posible del voltaje verdadero?

Respuesta 5

6.81V a 7.19V

6. Un multímetro digital de 50000 cuentas tiene una especificación de precisión de$\pm$ 0.1% y$\pm$ 4 recuentos. Si lee un voltaje de 7.00 voltios, ¿cuál es el rango posible del voltaje verdadero?

7. ¿Cuál es la carga en culombios de un millón de ($10^{12}$) electrones?

Respuesta 7

$1.602 \times 10^{-7} Coulombs$

8. ¿Cuál es la carga en culombios de$10^{15}$ electrones?

9. ¿Cuántos electrones serían necesarios para una carga de 20 culombios?

Respuesta 9

$1.248 \times 10^{20} electrons$

10. ¿Cuántos electrones serían necesarios para una carga de 1 microculombio?

11. Si una carga de 2 culombios pasa a través de un cable en 5 segundos, ¿cuál es la corriente?

Respuesta 11

0.4 Amperios

12. Si una carga de 300 miliculombios pasa a través de un cable en 0.1 segundos, ¿cuál es la corriente?

13. ¿Cuánta carga se debe transferir en 0.1 segundos para lograr una corriente de 5 amperios?

Respuesta 13

0.5 Coulombs

14. ¿Cuánta carga se debe transferir en 20 segundos para lograr una corriente de 10 microamperios?

15. Determine el voltaje resultante si se necesitan 2 julios para mover 10 culombios de carga.

Respuesta 15

0.2 Voltios

16. Determine el voltaje si se utilizan 15 julios para mover 0.5 culombios de carga.

17. ¿Cuánta energía se requiere para crear una diferencia de potencial de 10 voltios con una carga de 2 culombos?

Respuesta 17

20 Julios

18. ¿Cuánta energía se requiere para crear una diferencia de potencial de 50 milivoltios con una carga de 0.1 culomb?

19. ¿Cuál es el equivalente en potencia de dos caballos de fuerza (2 hp)?

Responder 19

1492 Watts

20. ¿Cuál es el equivalente de los caballos de fuerza de 1000 vatios?

21. Si un dispositivo consume 2 amperios de corriente de una batería de 12 voltios, determine la potencia entregada.

Respuesta 21

24 Watts

22. Si un dispositivo consume 10 miliamperios de corriente de una batería de 1.5 voltios, determine la potencia entregada.

23. Un motor de 2 hp extrae 1800 vatios de su fuente. Determinar su eficiencia.

Respuesta 23

82.9%

24. Un motor de 5 hp extrae 4.5 kw de su fuente. Determinar su eficiencia.

25. Un amplificador de potencia de audio está clasificado para 500 vatios de salida de audio máxima con una eficiencia del 80%. Determinar la cantidad de energía desperdiciada.

Responder 25

125 Watts

26. Un compresor extrae 10 amperios de corriente de una fuente de 120 voltios. Su potencia nominal es de 1 hp. Determinar la eficiencia.

27. Una aplicación requiere una batería para entregar 15 mA durante al menos 200 horas. Determine la clasificación requerida de amperios-hora (suponga que la batería puede suministrar el 100% de su energía).

Respuesta 27

3Ah

28. Determine la clasificación requerida para que una batería entregue 0.8 A durante al menos 30 horas.

29. Una cierta batería de 12 voltios tiene una clasificación de 6 Ah. Determine la duración esperada de la batería usando un consumo de 5 mA. Asumir 100% de consumo de energía.

Respuesta 29

1200 horas

30. Cierta batería AA tiene una clasificación de 800 mAh. Determine la duración esperada de la batería usando un consumo de 20 mA.

31. Supongamos que cierta pieza de material tiene una resistencia de 80 ohmios. Determine la nueva resistencia si se duplica la longitud de la pieza y no se cambian otros parámetros.

Respuesta 31

$160 \Omega$

32. Supongamos que cierta pieza de material tiene una resistencia de 2 k ohmios. Determine la nueva resistencia si el ancho y la altura de la pieza se duplican y no se cambian otros parámetros.

33. Supongamos que cierta pieza de material tiene una resistencia de 4 ohmios. Determinar la nueva resistencia si la resistividad se duplica y no se cambian otros parámetros.

Respuesta 33

$8 \Omega$

34. Supongamos que cierta pieza de material tiene una resistencia de 10 k ohmios. Determine la nueva resistencia si el largo, ancho y alto de la pieza están todos reducidos a la mitad.

35. Un determinado material tiene una resistividad de 100 ohm-centímetros. Determinar la resistencia de una pieza que tenga 1 cm de ancho, 0.5 cm de alto y 6 cm de largo.

Respuesta 35

$1200 \Omega$

36. Un determinado material tiene una resistividad de 2000 ohm-centímetros. Determinar la resistencia de una pieza que tenga 2 mm de ancho, 4 mm de alto y 10 mm de largo.

37. Una resistencia de 40 ohmios tiene una dimensión de 0.4 cm de ancho por 0.2 cm de alto por 1 cm de largo. Determinar la resistividad en ohmios-centímetros.

Respuesta 37

$3.2 \Omega \cdot cm $

38. Una resistencia de 5000 ohmios tiene dimensiones de 5 mm de ancho por 3 mm de alto por 6 mm de largo. Determinar la resistividad en ohmios-centímetros.

39. Una resistencia con el código de color amarillo-violeta-rojo-plata tiene un valor medido de 4806 ohmios. ¿Esta resistencia está dentro de la tolerancia? Como porcentaje, ¿qué tan lejos está del valor nominal?

Respuesta 39

sí, +2.26%

40. Una resistencia con el código de color naranja-naranja-amarillo-oro tiene un valor medido de 33.9 k ohmios. ¿Esta resistencia está dentro de la tolerancia? Como porcentaje, ¿qué tan lejos está del valor nominal?

41. Una resistencia con el código de color marrón-negro-naranja-plata tiene un valor medido de 9980 ohmios. ¿Esta resistencia está dentro de la tolerancia? Como porcentaje, ¿qué tan lejos está del valor nominal?

Respuesta 41

sí, -0.2%

42. Una resistencia con el código de color verde-azul-negro-oro tiene un valor medido de 50 ohmios. ¿Esta resistencia está dentro de la tolerancia? Como porcentaje, ¿qué tan lejos está del valor nominal?

43. Determinar el valor de las resistencias que se muestran en la Figura 2.10.1 (de izquierda a derecha: rojo-negro-amarillo, azul-gris-naranja, rojo-violeta-rojo-plata).

Respuesta 43

$200 k\Omega, 68 k\Omega, 2.7 k\Omega$

44. Determinar el valor de las resistencias que se muestran en la Figura 2.10.2 (de izquierda a derecha: rojo-rojo-naranja-oro, marrón-negro-rojo-oro, amarillo-violeta-naranja-plata).

45. Determinar el valor de las resistencias que se muestran en la Figura 2.10.3 (de izquierda a derecha: naranja-naranja-verde-plata, blanco-marrón-negro-plata, naranja-blanco-marrón-oro).

Respuesta 45

$3.3 M\Omega, 91\Omega, 390\Omega$

46. Determinar el valor de las resistencias que se muestran en la Figura 2.10.4 (de izquierda a derecha: plata-naranja-violeta-amarillo, verde-azul-amarillo-oro, oro-negro-naranja-amarillo).

47. Determine los valores máximos y mínimos permitidos de las resistencias que se muestran en la Figura 2.10.1 .

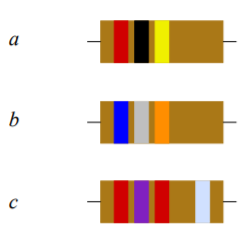
2.42.png

Figura 2.10.1

Respuesta 47

160k a 240k
54.4k a 81.6k
2.43k a 2.97k

48. Determine los valores máximos y mínimos permitidos de las resistencias que se muestran en la Figura 2.10.2 .

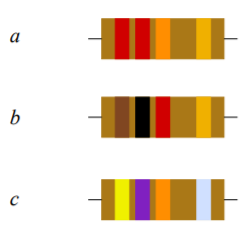
2.43.png

Figura 2.10.2

49. Determine los valores máximos y mínimos permitidos de las resistencias que se muestran en la Figura 2.10.3 .

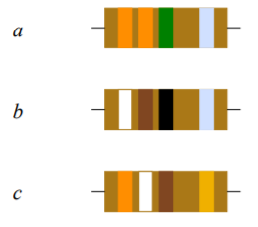
2.44.png

Figura 2.10.3

Respuesta 49

2.97M a 3.63M
81.9 a 100.1
370.5 a 409.5

50. Determine los valores máximos y mínimos permitidos de las resistencias que se muestran en la Figura 2.10.4 .

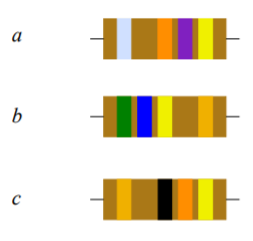
2.45.png

Figura 2.10.4

Diseño

51. Determine el código de color de la resistencia para los siguientes valores óhmicos usando 5% de tolerancia:

a) 47$\Omega$

b) 22 k$\Omega$

c) 390 k$\Omega$

d) 2.2 k$\Omega$

e) 560$\Omega$

Respuesta 51

amarillo-violeta-negro-dorado
Rojo-rojo-naranja-oro
Naranja-Blanco-Amarillo-Oro
marrón-rojo-oragne-dorado
violeta-verde-marrón-dorado

52. Determine el código de color de la resistencia para los siguientes valores óhmicos usando 10% de tolerancia:

a) 56$\Omega$

b) 33 k$\Omega$

c) 470 k$\Omega$

d) 1.2 k$\Omega$ e) 750$\Omega$

Desafío

53. Un transmisor de radio está clasificado para 100 vatios de salida máxima con una eficiencia del 90%. Si se alimenta desde una fuente de 120 voltios, determine el consumo de corriente.

Respuesta 53

Potencia de entrada:$frac{100 W}{0.9} = 111.11 W$
Actual:$I = frac{P}{V} = frac{111.11}{120}=0.93A$

54. Una cierta bombilla incandescente de 75 vatios produce 71 watts de calor y el resto en forma de luz. Determinar su eficiencia como dispositivo de iluminación y su eficiencia como dispositivo de calefacción.

55. Supongamos que una tostadora de 1800 vatios tarda 3 minutos en tostar un bagel “justo”. Si tostas un bagel todas las mañanas durante un año y la electricidad cuesta 15 céntimos/kWh, ¿cuánto habrás gastado en ese año para tostar bagels?

Respuesta 55

Minutos/año =$3 \times 365 = 1095 \: minutes$
Horas/año =$1095 \: minutes \times \frac{1 hour}{60 minutes} = 18.25 \: hours$
Energía =$1.8kW \times 18.25 \: hours = 32.85kWh$
Costo =$32.85kWh \times 15 \frac{cents}{kWh}+ = $4.93$

56. Suponga que puede comprar bombillas incandescentes estándar de 60 vatios por 50 centavos cada una y que cada una tiene una vida útil esperada de 1000 horas. En comparación, se puede comprar una bombilla LED que produce la misma cantidad de luz pero solo consume 7 watts. Las bombillas LED cuestan $5.50 cada una y tienen una vida útil esperada de 20,000 horas. Suponiendo que la electricidad cuesta 14 centavos/kWh, determine el costo total de funcionamiento de las luces incandescentes frente a los LEDs por 40,000 horas.

57. Dada una batería de 1.5 voltios con una clasificación de 500 mAh, ¿cuánta corriente puede producir continuamente durante 25 horas?.

58. Dada una batería de 9 voltios con una clasificación de 100 mAh, determinar el almacenamiento total de energía en julios.

59. Se utiliza un DMM de 2000 cuentas con$\pm$ 1% de precisión para medir la resistencia de un carrete de cable AWG 22. Si la medición es de 4.50$\Omega$, determine la longitud del cable y la posible inexactitud (en pies o metros).

60. Una longitud de cable AWG 26 está unida a un extremo de una longitud de cable AWG 32. La longitud total de los dos cables es de 200 metros. Determinar la longitud y resistencia de cada pieza si la resistencia total es de 75$\Omega$.