4.3: Combinación de componentes paralelos

Nuestro primer paso es determinar cómo combinar componentes paralelos para crear un solo componente equivalente. A diferencia de las conexiones en serie, esto puede llevar un poco más de tiempo.

Fuentes en Paralelo

Primero, las fuentes de voltaje no se colocan en paralelo como regla general, consulte la Figura 4.3.1 . La razón es porque una conexión en paralelo requiere el mismo voltaje en cada componente. Esto sería imposible de lograr con cada fuente tratando de mantener un voltaje diferente a través de los mismos dos nodos. Esto puede resultar en daños a las fuentes (por ejemplo, baterías explosivas). La principal excepción a esta regla es si las fuentes tienen el mismo potencial y el objetivo es extender la vida útil (por ejemplo, múltiples baterías de celdas D en paralelo).

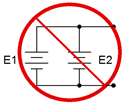
Figura 4.3.1 : No coloque fuentes de voltaje en paralelo.

Cuando se trata de fuentes de corriente, simplemente pueden sumarse, sin embargo, al igual que las fuentes de voltaje en serie, la polaridad es importante. Haciendo referencia a las tres fuentes de corriente paralelas en la Figura 4.3.2 , las fuentes media y derecha están bombeando corriente al nodo superior mientras que la fuente izquierda está alimentando el nodo inferior. También se puede pensar en la fuente izquierda como drenar el nodo superior. Así, estas tres fuentes juntas se comportan como una sola fuente de cinco amperios que alimenta el nodo superior (ocho amperios adentro, tres amperios fuera).

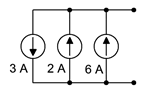
Figura 4.3.2 : Fuentes actuales en paralelo.

Resistencias en Paralelo

Cuando se coloca en paralelo, los valores de resistencia no agregan la forma en que lo hacen en las conexiones en serie. La razón de esto es obvia si observamos la ecuación de resistencia básica del Capítulo 2, Ecuación 2.11:

\[R = \frac{\rho l}{A} \nonumber \]

Si consideramos dos resistencias idénticas colocadas en paralelo, lado a lado como en la Figura 4.3.3 , el área efectiva se duplicaría manteniendo la resistividad y longitud sin cambios. El resultado combinado sería una reducción a la mitad de la resistencia de sólo una de ellas. Así vemos que colocar resistencias en paralelo da como resultado una disminución de la resistencia neta, lo opuesto al caso de la serie.

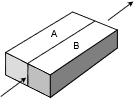
Figura 4.3.3 : Resistencias en paralelo.

Esta situación se simplifica si consideramos conductancia en lugar de resistencia. Recordando que la conductancia, G, es el recíproco de la resistencia, podemos reescribir la ecuación de resistencia:

\[G = \frac{A}{\rho l} \nonumber \]

Ahora podemos ver que el incremento de área crea un incremento proporcional en la conductividad. Si generalizamos esto para\(N\) resistencias encontramos que la conductancia equivalente de un grupo de resistencias paralelas es su suma:

\[G_{Total} = G_1+G_2+G_3+ \dots +G_N \label{4.2} \]

Como tratamos normalmente con valores de resistencia de componentes en lugar de valores de conductancia, la Ecuación\ ref {4.2} puede ser reescrita en términos de resistencia equivalente:

\[\frac{1}{R_{Parallel}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_N} \\ R_{Parallel} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_N}} \label{4.3} \]

Entre otras cosas, la Ecuación\ ref {4.3} nos dice que la resistencia equivalente de un grupo de resistencias paralelas siempre será menor que la resistencia más pequeña de ese grupo. También indica que si tenemos resistencias\(N\) idénticas de valor\(R\), el equivalente será\(R/N\) (por ejemplo, 3\( \Omega \) resistencias paralelas de 3.6 k son equivalentes a una sola\( \Omega \) resistencia de 1.2 k). Por conveniencia, es común utilizar dos líneas paralelas,\(||\), como una forma abreviada de decir “en paralelo con”, como en\(R_1 || R_2\). Además,\(||\) tiene mayor precedencia operativa que +.

Regla de Suma de Producto

Se puede crear un atajo práctico para dos resistencias paralelas a partir de la ecuación\ ref {4.3}. Comenzamos por escribir la versión para solo dos resistencias paralelas,

\[R_{Parallel} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} \nonumber \]

Multiplique la fracción por\(R_1\)\(R_2\) y simplifique:

\[R_{Parallel} = \frac{R_1 R_2}{R_1+R_2} \label{4.4} \]

Por razones obvias, la Ecuación\ ref {4.4} se conoce como la regla de producto-suma. Solo es aplicable a dos resistencias, sin embargo, se puede usar repetidamente en pares de resistencias dentro de grupos más grandes en lugar de usar la Ecuación\ ref {4.3}. Por ejemplo, un grupo de cuatro resistencias se puede reducir a dos pares, y luego esos dos equivalentes se pueden reducir como un tercer par. Esta puede ser una técnica útil para obtener estimaciones rápidas.

Podemos llevar la regla de producto-suma un paso más allá escribiendo\(R_2\) como un múltiplo de\(R_1\):

\[R_2 = N R_1 \nonumber \]

Sustituyendo esto en la Ecuación\ ref {4.4} produce:

\[R_{Parallel} = \frac{R_1 N R_1}{R_1+N R_1} \nonumber \]

\[R_{Parallel} = \frac{N R_1^2}{(N+1)R_1} \nonumber \]

\[R_{Parallel} = \frac{N}{N+1} R_1 \label{4.5} \]

La ecuación\ ref {4.5} es útil para estimaciones rápidas de pares de resistencias paralelas. Por ejemplo, si tenemos una\( \Omega \) resistencia de 24 k en paralelo con una\( \Omega \) resistencia de 8 k, esa es una relación (\(N\)) de 3:1. Por lo tanto, el equivalente será\(N/(N+1)\), o 3/4ths, de la resistencia más pequeña, dando 6 k\( \Omega \). De igual manera, un 180\( \Omega \) en paralelo con un 90\( \Omega \) produciría 2/3rds de 90\( \Omega \), o 60\( \Omega \).

Ejemplo 4.3.1

Un grupo de resistencias se coloca en paralelo como se muestra en la Figura 4.3.4 . Determinar el valor paralelo equivalente.

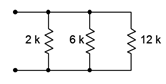
Figura 4.3.4 : Disposición de resistencias para Ejemplo 4.3.1 .

Existen varias rutas de solución. Los probaremos todos y compararemos. Primero, probemos la forma de conductancia:

\[R_{Parallel} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_N}} \nonumber \]

\[R_{Parallel} = \frac{1}{\frac{1}{2k \Omega } + \frac{1}{6k \Omega } + \frac{1}{12 k \Omega }} \nonumber \]

\[R_{Parallel} \approx 1.333 k \Omega \nonumber \]

También podríamos usar la regla de producto-suma dos veces. Primero usaremos la resistencia media y la más a la derecha (aunque cualquier emparejamiento lo haría, pero este emparejamiento es conveniente):

\[R_{23} = \frac{R_2 R_3}{R_2+R_3} \nonumber \]

\[R_{23} = \frac{6k \Omega 12 k \Omega }{6 k \Omega +12k \Omega } \nonumber \]

\[R_{23} = 4 k \Omega \nonumber \]

\[R_{Parallel} = \frac{R_1 R_{23}}{R_1+R_{23}} \nonumber \]

\[R_{Parallel} = \frac{2 k \Omega 4 k \Omega }{2 k \Omega +4k \Omega } \nonumber \]

\[R_{Parallel} \approx 1.333 k \Omega \nonumber \]

Finalmente, podríamos usar la técnica de ratio. Primero, considere el par de\( \Omega \) resistencias de 6 k\( \Omega \) y 12 k. Esa es una relación 2:1, por lo que el resultado será 2/3rds de la resistencia más pequeña, y 2/3rds de 6 k\( \Omega \) es 4 k\( \Omega \). La relación entre esta y la\( \Omega \) resistencia de 2 k también es 2:1, y 2/3rds de 2 k\( \Omega \) es aproximadamente 1.333 k\( \Omega \).

La técnica de relación resultó funcionar bien aquí debido a los convenientes valores de resistencia con relaciones enteras perfectas. Ese no siempre será el caso.