7.3: Análisis de malla
- Page ID
- 85995
En algunos aspectos, el análisis de malla es un espejo del análisis ganglionar. Mientras que el análisis nodal aprovecha KCL para crear una serie de ecuaciones de nodos que se utilizan para resolver tensiones de nodo, el análisis de malla utiliza KVL para crear una serie de ecuaciones de bucle que se pueden resolver para corrientes de malla. Una corriente de malla no debe confundirse con una corriente de derivación. Mientras que las corrientes de ramificación representan la corriente que fluye a través de un componente particular, las corrientes de malla se combinan para crear corrientes Es decir, la corriente a través de cualquier componente particular puede ser una corriente de malla individual o una combinación de dos corrientes de malla. Los circuitos que utilizan una disposición compleja serie-paralelo con múltiples fuentes de voltaje y/o corriente pueden resolverse usando esta técnica. Sin embargo, se limita a circuitos planos. Los circuitos planos son aquellos que se pueden dibujar en un plano plano sin tener ninguno de sus cables cruzados. En esencia, estos circuitos se pueden dibujar para que aparezcan como una serie de cristales de ventana. Los circuitos no planos pueden tener una apariencia 3D y en dicho circuito se vuelve imposible definir las ecuaciones de bucle ya que cualquier componente dado podría tener más de dos corrientes de malla.
Método General
Considere el circuito de la Figura 7.3.1 . Comenzamos designando una serie de bucles. Estos bucles deben ser de tamaño mínimo y cubrir todos los componentes al menos una vez. Por convención, los bucles se dibujan en sentido horario. No hay nada de magia en que estén en el sentido de las agujas del reloj, es solo cuestión de consistencia. La trayectoria de corriente a lo largo de un bucle se conoce como una corriente de malla. En el circuito de la Figura 7.3.1 tenemos dos bucles, y por lo tanto, dos corrientes de malla,\(I_1\) y\(I_2\). Tenga en cuenta que todos los componentes existen en al menos un bucle (y a veces en más de un bucle, como\(R_3\)). Dependiendo de los valores del circuito, una o más de las direcciones de estos bucles pueden ser de hecho opuestas a la realidad. Esto no es un problema. Si este es el caso, las corrientes aparecerán como valores negativos, y así sabemos que realmente están fluyendo en sentido antihorario.
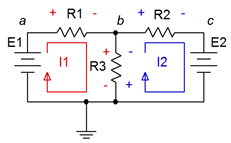
Figura 7.3.1 : Circuito para análisis de malla.
Comenzamos por escribir ecuaciones KVL para cada bucle.
\[\text{Loop 1: } E_1 = \text{ voltage across } R_1 + \text{ voltage across } R_3 \nonumber \]
\[\text{Loop 2: }−E_2 = \text{ voltage across } R_2 + \text{ voltage across } R_3 \nonumber \]
\[(E_2 \text{ is negative as } I_2 \text{ is drawn flowing out of its negative terminal.)} \nonumber \]
Amplíe los términos de voltaje usando la ley de Ohm.
\[\text{Loop 1: } E_1 = I_1 \cdot R_1 + (I_1 − I_2) R_3 \nonumber \]
\[\text{Loop 2: } −E_2 = I_2 \cdot R_2 + (I_2 − I_1) R_3 \nonumber \]
Ampliar y recopilar términos rendimientos:
\[\text{Loop 1: } E_1 = (R_1 + R_3) I_1 − R_3 \cdot I_2 \nonumber \]
\[\text{Loop 2: }: −E_2 = R_3 \cdot I_1 + (R_2 + R_3) I_2 \nonumber \]
Suponiendo que se conocen los valores de resistencia y los voltajes de fuente, tenemos dos ecuaciones con dos incógnitas. Estos se pueden resolver para\(I_1\) y\(I_2\) utilizando técnicas de solución de ecuaciones simultáneas como determinantes o eliminación de Gauss-Jordan.
Encuentra\(V_b\) y\(V_{bc}\) para el circuito de Figura 7.3.2 .
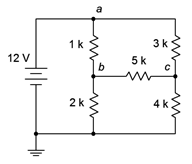
Figura 7.3.2 : Circuito por ejemplo 7.3.1 .
El primer paso es definir un conjunto de bucles en sentido horario que sean de tamaño mínimo y que cubran todos los componentes. Estos bucles se dibujan en la Figura 7.3.3 . Además, las polaridades de las caídas de voltaje producidas por estas corrientes se dibujan junto a los componentes en el mismo color para una fácil identificación. Tenga en cuenta que algunos componentes ven solo una corriente, como la\( \Omega \) resistencia de 3 k que solo ve\(I_2\); y algunos ven dos corrientes en direcciones opuestas, como la\( \Omega \) resistencia de 5 k que ve ambas\(I_2\) y\(I_3\). Con múltiples direcciones de corriente fluyendo a través de un solo componente, obedecer las polaridades de voltaje resultantes se vuelve muy importante.
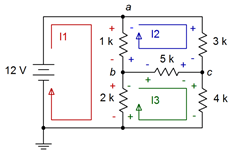
Figura 7.3.3 : Circuito de Ejemplo 7.3.1 con bucles de corriente y polaridades agregadas.
Ahora escribimos sumaciones KVL alrededor de cada bucle. Si la corriente que pasa a través de un componente ve una polaridad de + a − entonces esto se cuenta como una caída de voltaje mientras que el reverso cuenta como un aumento de voltaje. Esto es cierto incluso para fuentes de voltaje (es decir, una fuente de voltaje puede aparecer negativa en un bucle y positiva en otro).
\[\sum V_{rises} = \sum V_{drops} \nonumber \]
\[\text{Loop 1: } 12 V = V_{1k}+V_{2k} \nonumber \]
\[\text{Loop 2: } 0V = V_{3k}+V_{5k}+V_{1k} \nonumber \]
\[\text{Loop 3: } 0V = V_{5k}+V_{4k}+V_{2k} \nonumber \]
Estos se expanden usando la ley de Ohm. La corriente para el bucle en consideración se considera positiva mientras que cualquier corriente opuesta (es decir, mallada) se considera negativa:
\[\text{Loop 1: } 12 V = 1k(I_1 −I_2 )+2 k(I_1 −I_2 ) \nonumber \]
\[\text{Loop 2: } 0V = 3 k(I_2 )+5k(I_2 −I_3 )+1k(I_2 −I_1 ) \nonumber \]
\[\text{Loop 3: } 0V = 5 k(I_3 −I_2 )+4k(I_3 )+2k(I_3 −I_1 ) \nonumber \]
Se amplían los términos:
\[\text{Loop 1: } 12 V = 1k I_1 −1 k I_2+2 k I_1 −2 k I_3 \nonumber \]
\[\text{Loop 2: } 0V = 3 k I_2+5k I_2 −5k I_3+1k I_2 −1 k I_1 \nonumber \]
\[\text{Loop 3: } 0V = 5 k I_3 −5k I_2+4k I_3+2k I_3 −2k I_1 \nonumber \]
Se agrupan términos similares, creando de nuevo columnas alineadas para los coeficientes actuales:
\[\text{Loop 1: } 12 V = (1k+2k)I_1 −1 k I_2 −2 k I_3 \nonumber \]
\[\text{Loop 2: } 0V = −1k I_1+(3 k+5k+1k) I_2 −5k I_3 \nonumber \]
\[\text{Loop 3: } 0V = −2k I_1 −5k I_2+(5k+4k+2k)I_3 \nonumber \]
Lo que simplifica a:
\[\text{Loop 1: } 12 V = 3k I_1 −1k I_2 −2 k I_3 \nonumber \]
\[\text{Loop 2: } 0V = −1k I_1 +9 k I_2 −5k I_3 \nonumber \]
\[\text{Loop 3: } 0V = −2k I_1 −5k I_2+11 k I_3 \nonumber \]
Tenga en cuenta que tenemos simetría diagonal. La solución es\(I_1\) = 5.729 mA,\(I_2\) = 1.6258 mA y\(I_3\) = 1.7806 mA. Para encontrar\(V_b\) necesitamos encontrar la corriente neta a través de la\( \Omega \) resistencia de 2 k. Eso es\(I_1 − I_3\), o 5.729 mA − 1.7806 mA, que es 3.9484 mA. Cuando se multiplica por 2 k\( \Omega \) encontramos\(V_b\) = 7.8968 voltios. Del mismo modo,\(V_{bc} = (I_3 − I_2)\) 5 k\( \Omega \) = (1.7806 mA − 1.6258 mA) 5 k\( \Omega \), o 774 mV.
Simulación por Computadora
Para verificar los resultados del análisis, el circuito se ingresa a un simulador y se coloca un voltímetro virtual a través de la\( \Omega \) resistencia de 5 k. Esto se muestra en la Figura 7.3.4 . Los resultados concuerdan muy bien con el análisis original.
Por agradable que sea esto, en un circuito práctico necesitamos preocuparnos por los efectos de la tolerancia de los componentes. Sería extraordinariamente extraño si durante la producción cada resistencia fuera igual precisamente al valor nominal especificado. En realidad, cada resistencia tendrá una tolerancia declarada. Por lo tanto, con las cinco resistencias cambiando ligeramente de una unidad a otra, debemos esperar que las corrientes y tensiones también varíen. La pregunta es, ¿cuál sería un spread típico? Esto se puede abordar a través de un análisis de Montecarlo. Este análisis es, de hecho, una serie de simulaciones. Cada simulación utiliza valores de componentes aleatorios que se encuentran dentro de la dispersión de tolerancia establecida. Por ejemplo, si especificamos que la\( \Omega \) resistencia de 1 k tiene una tolerancia del 5%, entonces la resistencia real utilizada para una simulación será un valor generado aleatoriamente entre 950\( \Omega \) y 1050\( \Omega \). Luego indicamos cuántos ensayos nos gustaría, cada uno usando sus propios valores aleatorios únicos para cada componente.
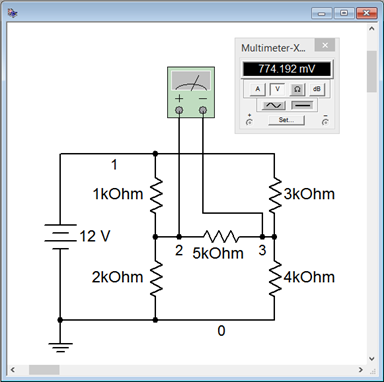
Figura 7.3.4 : Circuito de la Figura 7.3.2 en un simulador con un voltímetro virtual.
En la Figura {{Template.index (ID:5)} se muestran los resultados de un análisis de Monte Carlo utilizando la simulación de punto operativo DC. Se generaron diez ensayos aleatorios para el valor de\(V_b\). A cada una de las cinco resistencias se le asignó una tolerancia del 5%. Como se puede ver, pueden resultar valores de voltaje tanto por encima como por debajo de la simulación nominal.
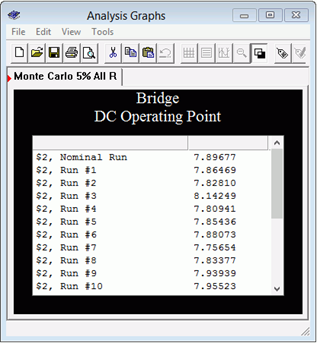
Figura 7.3.5 : Resultados del análisis de Montecarlo para el circuito de la Figura 7.3.2 .
Método de Inspección
Al igual que el análisis nodal, existe un método para generar las ecuaciones por inspección. Simplemente concéntrese en un bucle, que llamaremos el bucle bajo inspección, y haga las siguientes preguntas: ¿cuál es el voltaje total de la fuente en este bucle? Esto produce la constante de voltaje para la ecuación. Luego suma todos los valores de resistencia en el bucle bajo inspección. Esto arroja el coeficiente para ese término actual. Para los coeficientes de corriente restantes en esta ecuación, sumar las resistencias que están en común entre el bucle bajo inspección y los otros bucles, respectivamente. Estos valores siempre serán negativos. Repita este proceso para todos los bucles, con cada bucle a su vez convirtiéndose en el bucle bajo inspección. Como fue el caso del análisis nodal, el conjunto de ecuaciones producidas debe exhibir simetría diagonal, es decir, si se dibuja una diagonal de la parte superior izquierda a la inferior derecha a través de los\(I_R\) pares, entonces los coeficientes encontrados por encima de la diagonal tendrán que coincidir con los que se encuentran debajo de la diagonal.
Si bien es posible extender esta técnica para incluir fuentes de corriente, a menudo es más fácil y menos propenso a errores convertir las fuentes de corriente en fuentes de voltaje y continuar con el método de inspección directa descrito anteriormente. De cualquier manera, es importante recordar que el número de bucles determina el número de ecuaciones a resolver.
Encuentra\(V_c\) para el circuito de la Figura 7.3.6 .
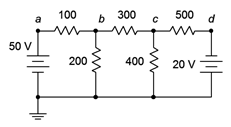
Figura 7.3.6 : Circuito por ejemplo 7.3.2 .
Primero, etiquetaremos los bucles, como se muestra en la Figura 7.3.7 .
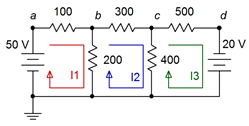
Figura 7.3.7 : Circuito de Ejemplo 7.3.2 con bucles actuales identificados.
Ahora, comenzando con el bucle 1, suma todas las fuentes de voltaje en este bucle. Eso es +50 voltios. En segundo lugar, sumar todas las resistencias en este bucle. Eso son 100\( \Omega \) + 200\( \Omega \), o 300\( \Omega \). Este es el coeficiente para el\(I_1\) término. El coeficiente para el\(I_2\) término es la suma de todas las resistencias que están en común entre los bucles 1 y 2. Eso es sólo la\( \Omega \) resistencia 200. El coeficiente para el\(I_3\) término sería la suma de todas las resistencias que están en común entre el bucle 1 y el bucle 3. En este circuito, no hay ninguno así que el coeficiente es cero. La primera ecuación es:
\[\text{Loop 1: } 50 V = 300I_1 −200I_2 −0I_3 \nonumber \]
Repita el proceso para los bucles 2 y 3:
\[\text{Loop 2: } 0V = −200I_1 +900I_2 −400I_3 \nonumber \]
\[\text{Loop 3: } 20V = −0I_1 −400I_2 +900I_3 \nonumber \]
Tenga en cuenta que la fuente de 20 voltios se muestra positiva debido a la dirección de\(I_3\) (dentro del terminal negativo y fuera del terminal positivo).
Según se requiera, tenemos simetría diagonal. La solución es\(I_1\) = 214.47 mA,\(I_2\) = 71.698 mA y\(I_3\) = 54.088 mA. \(V_c\)es la corriente neta a través de la\( \Omega \) resistencia 400 veces 400\( \Omega \). La corriente neta es\(I_2 − I_3\), o 71.698 mA − 54.088 mA, que es 17.61 mA. Cuando se multiplica por 400\( \Omega \) encontramos\(V_b\) = 7.044 voltios. Tenga en cuenta que usamos\(I_2 − I_3\) y no\(I_3 − I_2\). La razón es porque estamos tratando de encontrar el voltaje de nodo\(c\) a tierra, y\(I_2\) es la corriente que fluye en esa dirección. En contraste, el uso\(I_3 − I_2\) produciría el voltaje de tierra a nodo\(c\); la misma magnitud pero signo opuesto.
Como comprobación cruzada, KVL establece que\(V_c + V_{500}\) tiene que ser igual a la fuente de −20 voltios. La caída a través del 500\( \Omega \) es de 54.088 mA por 500\( \Omega \), o 27.044 voltios de izquierda a derecha. Comenzando en el nodo\(c\) de 7.044 voltios y luego cayendo 27.044 voltios produce − 20 voltios como se esperaba.
Supermesh
A veces puede encontrarse con una fuente de corriente que no tiene resistencia interna asociada, como la que se encuentra en el circuito de la Figura 7.3.8 . Esto es similar a la situación vista previamente bajo análisis nodal donde una fuente de voltaje no tiene una resistencia interna especificada. Hay dos formas de resolver esta situación. El primero es agregar una resistencia muy grande en paralelo con la fuente de corriente y luego realizar una conversión de fuente en el par para que se pueda seguir el método de inspección de malla. Cuanto mayor sea el valor de esta resistencia, mayor será la precisión que se obtiene. Como regla general debe ser, como mínimo, al menos un par de órdenes de magnitud más grande que cualquier resistencia circundante, y preferiblemente mayor. El segundo método es usar supermesh. Una supermalla es un bucle de malla más grande que contiene otros bucles de malla dentro de él.
Considere el circuito que se muestra en la Figura 7.3.8 . En el centro tenemos una fuente de corriente,\(I_s\), que carece de una resistencia interna asociada. Dos bucles de malla tradicionales,\(I_1\) y\(I_2\), están etiquetados como de costumbre. El problema aquí es que no podemos usar una caída de\(IR\) voltaje basada en la ley de Ohm para\(V_b\). No tenemos forma de expresar esto ya que el voltaje a través\(I_s\) es un desconocido. Por otro lado, lo que sí sabemos es que\(I_s\) debe igualar la combinación de las corrientes tradicionales de malla\(I_1\) y\(I_2\). Es decir, desde la perspectiva del primer bucle,\(I_s = I_1 − I_2\). Recuerde, una o ambas corrientes de malla podrían ser negativas, y así girar en sentido antihorario.
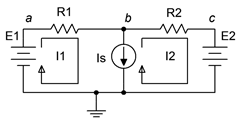
Figura 7.3.8 : Circuito para supermesh.
En este punto invocamos la idea de un bucle supermesh. Primero, reemplazamos la fuente de corriente infractora con su resistencia interna ideal (una abierta). Se dibuja el bucle supermesh que abarca los dos bucles originales. Esto se muestra en la Figura 7.3.9 . El bucle supermesh se dibuja en rojo y se etiqueta.
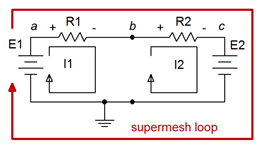
Figura 7.3.9 : Supermesh etiquetada.
Ahora realizamos una suma KVL alrededor del bucle supermesh, similar a lo que hemos hecho anteriormente. La diferencia esta vez es que necesitamos reconocer que cada uno de los componentes ve una de las corrientes de malla originales; es decir,\(I_1\) o\(I_2\) en este caso. No resolvemos para una corriente de supermalla, simplemente usamos la supermalla para definir el bucle para la suma KVL. La suma sigue:
\[ \sum V_{rises} = \sum V_{drops} \nonumber \]
\[E_1 = V_{R1}+V_{R2}+E_2 \nonumber \]
Las caídas de voltaje a través de las resistencias se pueden expandir usando la ley de Ohm, usando la corriente de malla original asociada con cada resistencia.
\[E_1 −E_2 = I_1 R_1+I_2 R_2 \nonumber \]
Por inspección,
\[I_s = I_1 −I_2 \text{ or} \nonumber \]
\[I_2 = I_1 −I_s \nonumber \]
Ahora tenemos dos ecuaciones con dos incógnitas y podemos resolver por\(I_1\) y\(I_2\). Este procedimiento se ilustra en el siguiente ejemplo.
Encuentra\(V_b\) para el circuito de Figura 7.3.10 .
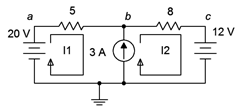
Figura 7.3.10 : Circuito para Ejemplo 7.3.3 .
Primero, etiquetaremos los bucles, como se muestra en la Figura 7.3.11 .
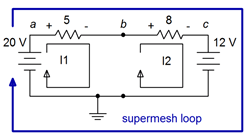
Figura 7.3.11 : Circuito de la Figura 7.3.10 con supermalla etiquetada.
A continuación, realizaremos una suma KVL alrededor del bucle supermesh.
\[\sum V_{rises} = \sum V_{drops} \nonumber \]
\[20 V = V_{R1}+V_{R2} +12V \nonumber \]
Expandir usando la ley de Ohm y reorganizar:
\[20 V −12 V = 5 \Omega I_1+8 \Omega I_2 \nonumber \]
\[8V = 5 \Omega I_1+8 \Omega I_2 \nonumber \]
Por inspección sabemos
\[3A = I_2 −I_1 \text{ or} \nonumber \]
\[I_2 = I_1+3A \nonumber \]
Podemos sustituir esta expresión en la expresión de supermesh anterior y resolver para I1:
\[8 V = 5 \Omega I_1+8 \Omega I_2 \nonumber \]
\[8 V = 5 \Omega I_1+8 \Omega (I_1+3A) \nonumber \]
\[8 V = 5 \Omega I_1+8 \Omega I_1+24 V \nonumber \]
\[−16 V = 13 \Omega I_1 \nonumber \]
\[I_1 \approx−1.231A \nonumber \]
Así,\(I_2\) = −1.231 A + 3 A, o 1.769 A. Para determinar simplemente\(V_b\) restamos la caída a través de la\( \Omega \) resistencia 5 de la fuente de 20 voltios.
\[V_b = 20 V − I_1 5 \Omega \nonumber \]
\[V_b = 20 V − (−1.231 A)5 \Omega \nonumber \]
\[V_b \approx 26.15 V \nonumber \]
Como comprobación cruzada, también podríamos agregar el voltaje a través de la\( \Omega \) resistencia 8 a la fuente de 12 voltios:
\[V_b = 12V +I_2 8 \Omega \nonumber \]
\[V_b = 12V +1.769 A 8 \Omega \nonumber \]
\[V_b \approx26.15 V \nonumber \]
Comparación de Nodal y Mesh
En comparación con el análisis nodal, el análisis de malla tiene la ventaja de tratar con resistencias en lugar de conductancias al escribir el sistema de ecuaciones. Además, el método de inspección de malla funciona con fuentes de voltaje, lo que tiende a ser conveniente para muchos circuitos, mientras que el método de inspección nodal requiere fuentes de corriente. En el lado negativo, el conjunto resultante de corrientes de malla requiere un procesamiento adicional para encontrar corrientes de ramificación o voltajes de nodo, mientras que el análisis nodal produce voltajes de nodo directamente sin procesamiento adicional. La malla también tiene la desventaja de estar limitada a circuitos planos mientras que no hay tales límites para nodal.


