Saltar al contenido principal
LibreTexts Español

8.6: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    86126

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Análisis

    1. Para el circuito que se muestra en la Figura 8.6.1 , determine la capacitancia efectiva.

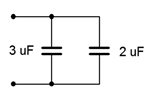
    clipboard_e81f7e6e091a00b9ae5bbcdcf00f0c7dc.png

    Figura 8.6.1

    2. Determinar la capacitancia efectiva de la configuración mostrada en la Figura 8.6.2 .

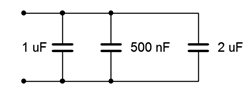
    clipboard_e4314808ccef91d45b0d1211d126b9aab.png

    Figura 8.6.2

    3. Dada la red de condensadores que se muestra en la Figura 8.6.3 , determinar el valor efectivo.

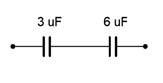
    clipboard_e64dfcf53dd3f4828c493da9ebcbe18c3.png

    Figura 8.6.3

    4. Determinar la capacitancia efectiva de la red que se muestra en la Figura 8.6.4 .

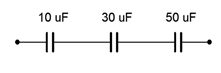
    clipboard_ed627b243ed361c86360ade9fa179e7c8.png

    Figura 8.6.4

    5. Determine el voltaje a través de cada condensador para el circuito que se muestra en la Figura 8.6.5 .

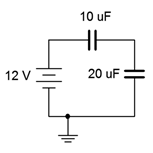
    clipboard_e07ba7e553ab742f52fd716a57e3e3b12.png

    Figura 8.6.5

    6. Determine el voltaje a través de cada condensador para el circuito que se muestra en la Figura 8.6.6 .

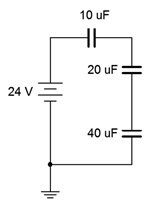
    clipboard_eb32395ee995d0dc397497724948843a4.png

    Figura 8.6.6

    7. Determine el voltaje inicial a través de cada componente para el circuito que se muestra en la Figura 8.6.7 .

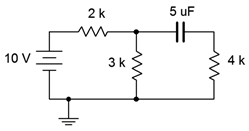
    clipboard_e0b1c41fe683d2dd3641f906a86ca9523.png

    Figura 8.6.7

    8. Dada la red que se muestra en la Figura 8.6.7 , determinar la tensión de estado estacionario a través de cada componente.

    9. Para el circuito que se muestra en la Figura 8.6.8 , determine el voltaje del condensador 3 microsegundos después de que se encienda la alimentación.

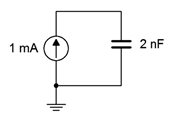
    clipboard_ec9395ed2dbef6663c8c24220485e8ae3.png

    Figura 8.6.8

    10. Para el circuito que se muestra en la Figura 8.6.9 , determine la tensión del condensador 5 segundos después de que se encienda la alimentación.

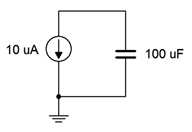
    clipboard_eb2c326ee49d3d752b36f001e3d15f73a.png

    Figura 8.6.9

    11. Determine la constante de tiempo y el tiempo requerido para alcanzar el estado estacionario para el circuito que se muestra en la Figura 8.6.10 .

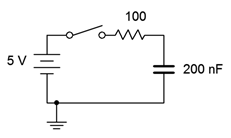
    clipboard_e30d1b6ca93b1815b3edcbdebe31874ea.png

    Figura 8.6.10

    12. Para el circuito que se muestra en la Figura 8.6.10 , determine el voltaje del condensador y la corriente circulante 20 microsegundos y 100 milisegundos después de que se lance el interruptor.

    13. Dado el circuito que se muestra en la Figura 8.6.11 , determinar el voltaje del condensador y la corriente circulante 200 milisegundos y 10 segundos después de que se lanza el interruptor.

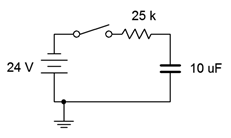
    clipboard_ec2d34ebbfbde33e3cb240e47bb9e2f62.png

    Figura 8.6.11

    14. Determine la constante de tiempo y el tiempo requerido para alcanzar el estado estacionario para el circuito que se muestra en la Figura 8.6.11 .

    15. Determine la constante de tiempo y el tiempo requerido para alcanzar el estado estacionario para el circuito mostrado en la Figura 8.6.12 , cambiar la posición 1.

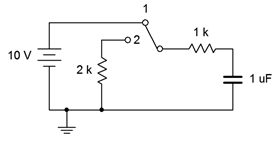
    clipboard_e876134bbb813459a5b2189643906117e.png

    Figura 8.6.12

    16. Determine las constantes de tiempo de carga y descarga para el circuito que se muestra en la Figura 8.6.13 .

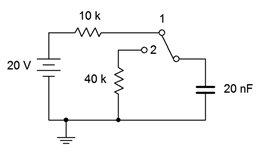
    clipboard_e8f670bb41876d029bd0ba752573e6568.png

    Figura 8.6.13

    17. Dado el circuito que se muestra en la Figura 8.6.12 , determine el voltaje del condensador 10 milisegundos después de que se encienda la alimentación. En este punto, el interruptor se lanza a la posición 2. Determine cuánto tiempo tardará el condensador en descargarse a casi cero voltios.

    18. Para el circuito que se muestra en la Figura 8.6.13 , determine el voltaje del condensador 400 microsegundos después de que se encienda la alimentación. En este punto, el interruptor se lanza a la posición 2. Determine cuánto tiempo tardará el condensador en descargarse a casi cero voltios.

    19. Determine la constante de tiempo y el tiempo requerido para alcanzar el estado estacionario para el circuito mostrado en la Figura 8.6.14 , cambiar la posición 1.

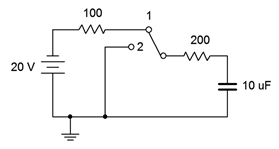
    clipboard_e90d969fa806e2f39369b8e803689eb9c.png

    Figura 8.6.14

    20. Dado el circuito que se muestra en la Figura 8.6.14 , determine el voltaje del condensador 12 milisegundos después de que se encienda la alimentación. En este punto, el interruptor se lanza a la posición 2. Determine cuánto tiempo tardará el condensador en descargarse a casi cero voltios.

    Diseño

    21. Dado el circuito de la Figura 8.6.10 , determinar un nuevo valor de resistencia de tal manera que se alcance el estado estacionario en 2 milisegundos.

    22. Dado el circuito de la Figura 8.6.11 , determinar un nuevo valor de resistencia de tal manera que se alcance el estado estacionario en 5 segundos.

    23. Cuando se enciende un amplificador de audio, la sobretensión puede causar un pop audible desde el altavoz. Para evitar esto, los amplificadores a menudo se conectan al altavoz a través de un relé. El relé se energiza para conectar el altavoz una vez que la salida se ha asentado, típicamente unos segundos después de que se aplique la energía. Este retraso se puede crear a través de una red RC. Supongamos que el circuito de accionamiento es de 5 voltios y el relé se activa a 4 voltios. Además, la resistencia de carga asociada es de 10 k\(\Omega\). Determinar la capacitancia requerida para lograr un tiempo de retardo de 2 segundos.

    Desafío

    24. Determine la constante de tiempo y el tiempo requerido para alcanzar el estado estacionario para el circuito que se muestra en la Figura 8.6.15 .

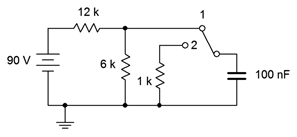
    clipboard_e48f7d52adf16a1b1cbbfb6524dc0c6f2.png

    Figura 8.6.15

    25. Para el circuito que se muestra en la Figura 8.6.15 , determine el voltaje del condensador 1 segundo después de que se encienda la alimentación. En este punto, el interruptor se lanza a la posición 2. Determine cuánto tiempo tardará el condensador en descargarse a casi cero voltios.

    Simulación

    26. Realizar un análisis transitorio para verificar el tiempo hasta el estado estacionario de la Figura 8.6.10 (problema 11).

    27. Realizar un análisis transitorio para verificar el tiempo hasta el estado estacionario de la Figura 8.6.11 (problema 14).

    28. Utilizar un análisis transitorio para verificar el diseño del problema 21.

    29. Utilizar un análisis transitorio para verificar el diseño del problema 22.

    30. Utilice un análisis transitorio para verificar el funcionamiento del circuito que se muestra en la Figura 8.6.15 como se especifica en el problema 25. Es posible que desee hacer esto como dos simulaciones separadas, una para cada posición del interruptor, con la segunda posición usando un condensador precargado.

    This page titled 8.6: Ejercicios is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by James M. Fiore via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.