9.3: Análisis inicial y de estado estacionario de circuitos RL
- Page ID
- 86081
Al analizar los circuitos resistor-inductor, recuerde que la corriente a través de un inductor no puede cambiar instantáneamente ya que esto requeriría una fuente de voltaje infinita. Cuando un circuito es energizado por primera vez, la corriente a través del inductor seguirá siendo cero, lo cual es característico de las aperturas. Una vez en estado estacionario, la corriente se ha nivelado y por lo tanto el voltaje a través del inductor se acercará a cero, lo que es característico de los cortocircuitos. Así, podemos exponer el comportamiento general de los inductores al inicio y al final del ciclo de carga:
\[\text{For DC analysis, initially inductors appear as opens.} \label{9.11} \]
\[\text{At steady-state, inductors appear as shorts.} \label{9.12} \]
Esto es lo contrario de lo que se vio con los capacitores. Por ejemplo, en el circuito de la Figura 9.3.1 , inicialmente\(L\) está abierto, dejándonos con\(R_1\) y\(R_2\) en serie con la fuente,\(E\). En estado estacionario, corta\(L\) hacia fuera, dejando\(R_1\) en serie con la combinación paralela de\(R_2\) y\(R_3\). Todos los inductores prácticos exhibirán alguna resistencia interna, por lo que a menudo es mejor pensar en un inductor como una inductancia ideal con una pequeña resistencia (\(R_{coil}\)) en serie con él.
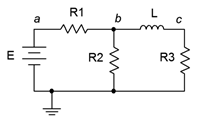
Figura 9.3.1 : Circuito RL básico.
Suponiendo que la corriente inicial a través del inductor es cero en el circuito de la Figura 9.3.2 , determine el voltaje a través de la\( \Omega \) resistencia de 2 k cuando se aplique energía y después de que el circuito haya alcanzado el estado estacionario. Dibuja cada uno de los circuitos equivalentes.
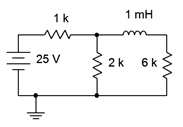
Figura 9.3.2 : Circuito por ejemplo 9.3.1 .
Primero, volveremos a dibujar el circuito para el equivalente de estado inicial. Para ello, abra el inductor. El nuevo equivalente se muestra en la Figura 9.3.3 . Al abrir el inductor, la\( \Omega \) resistencia de 6 k se ha eliminado del circuito y no ve voltaje. Lo que nos queda es un divisor de voltaje entre la fuente y las\( \Omega \) resistencias de 1 k\( \Omega \) y 2 k.
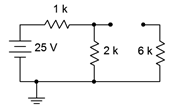
Figura 9.3.3 : Equivalente al estado inicial del circuito de la Figura 9.3.2 .
Usando la regla del divisor de voltaje,
\[V_{2k} = E \frac{R_x}{R_x+R_y} \nonumber \]
\[V_{2k} = 25 V \frac{2k \Omega}{ 2k \Omega +1 k \Omega} \nonumber \]
\[V_{2k} \approx 16.67V \nonumber \]
Para el estado estacionario, redibujamos usando un corto en lugar del inductor, como se muestra en la Figura 9.3.4 . Aquí tenemos otro divisor de voltaje, esta vez entre la\( \Omega \) resistencia de 1 k y la combinación paralela de 2 k\( \Omega \) y 6 k\( \Omega \), o 1.5 k\( \Omega \).
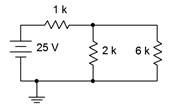
Figura 9.3.4 : Equivalente en estado estacionario del circuito de la Figura 9.3.2 .
\[V_{2k} = E \frac{R_x}{R_x+R_y} \nonumber \]
\[V_{2k} = 25 V \frac{1.5k \Omega}{ 1.5k \Omega +1k \Omega} \nonumber \]
\[V_{2k} = 15V \nonumber \]
Simulación por Computadora
Para verificar los resultados del Ejemplo 9.3.1 , el circuito se introduce en un simulador como se muestra en la Figura 9.3.5 . Se ejecuta un análisis de punto de operación DC y los resultados se muestran en la Figura 9.3.6 .
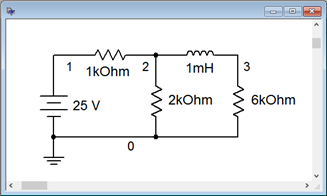
Figura 9.3.5 : Circuito de la Figura 9.3.2 en un simulador.
El potencial de estado estacionario en el nodo 2 corresponde al voltaje a través de la\( \Omega \) resistencia de 2 k y concuerda con el cálculo teórico de 15 voltios. Tenga en cuenta que el nodo 3 también es de 15 voltios, lo que indica que el voltaje de estado estacionario a través del inductor es cero, lo que significa que se está comportando como un corto, exactamente como se esperaba.
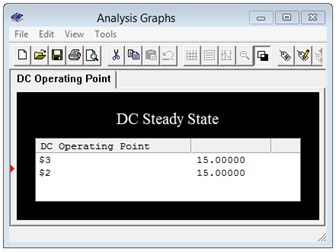
Figura 9.3.6 : Resultados de simulación para el circuito de la Figura 9.3.2 .


