9.4: Análisis inicial y de estado estacionario de circuitos RLC

Última actualización
Guardar como PDF

Page ID: 86067

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Al analizar los circuitos resistor-inductor-condensador, recuerde que el voltaje del condensador no puede cambiar instantáneamente, así, inicialmente, los condensadores se comportan como un cortocircuito. Una vez que el condensador ha sido cargado y está en estado estacionario, se comporta como un circuito abierto. Esto es opuesto al inductor. Como hemos visto, inicialmente un inductor se comporta como un abierto, pero una vez alcanzado el estado estacionario, se comporta como un corto. Por ejemplo, en el circuito de la Figura 9.4.1 , inicialmente\(L\) está abierto y\(C\) es un corto, dejándonos con\(R_1\) y\(R_2\) en serie con la fuente,\(E\). En estado estacionario, los\(L\) pantalones cortos hacia fuera ambos\(C\) y\(R_2\), dejando todo caer\(E\) a través\(R_1\). Para una mayor precisión, reemplace el inductor con una inductancia ideal en serie con el\(R_{coil}\) valor correspondiente. Del mismo modo, los capacitores prácticos pueden considerarse como una capacitancia ideal en paralelo con una resistencia muy grande (fuga).

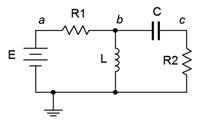
Figura 9.4.1 : Circuito RLC básico.

Ejemplo 9.4.1

Suponiendo que la corriente inicial a través del inductor es cero y el condensador está descargado en el circuito de la Figura 9.4.2 , determine la corriente a través de la\(\Omega\) resistencia de 2 k cuando se aplique potencia y después de que el circuito haya alcanzado el estado estacionario. Dibuja cada uno de los circuitos equivalentes.

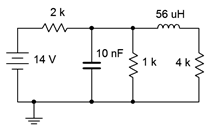
Figura 9.4.2 : Circuito por ejemplo 9.4.1 .

Para el equivalente de estado inicial abrimos el inductor y cortocircuitamos el condensador. El nuevo equivalente se muestra en la Figura 9.4.3 . El condensador cortocircuitado elimina todo a su derecha del circuito. Todo lo que queda es la fuente y la\(\Omega\) resistencia de 2 k.

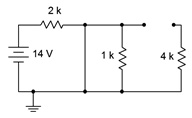
Figura 9.4.3 : Equivalente al estado inicial del circuito de la Figura 9.4.2 .

Podemos encontrar la corriente a través de la\(\Omega\) resistencia de 2 k usando la ley de Ohm.

\[I_{2k} = \frac{E}{R} \nonumber \]

\[I_{2k} = \frac{14 V}{2k \Omega} \nonumber \]

\[I_{2k} = 7 mA \nonumber \]

El estado estacionario se vuelve a dibujar en la Figura 9.4.4 , usando un cortocircuito en lugar del inductor, y un circuito abierto para el condensador. Nos quedamos con una resistencia de 2 k\(\Omega\) en serie con la combinación paralela de 1 k\(\Omega\) y 4 k\(\Omega\), o 2.8 k\(\Omega\) en total.

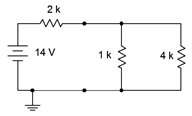
Figura 9.4.4 : Equivalente en estado estacionario del circuito de la Figura 9.4.2 .

\[I_{2k} = \frac{E}{R} \nonumber \]

\[I_{2k} = \frac{14 V}{2.8k \Omega} \nonumber \]

\[I_{2k} = 5mA \nonumber \]