9.5: Respuesta Transitoria de Circuitos RL
- Page ID
- 86075
La respuesta transitoria de los circuitos RL es casi la imagen especular de la de los circuitos RC. Para apreciar esto, considere el circuito de la Figura 9.5.1 .
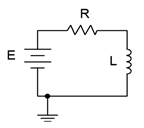
Figura 9.5.1 : Circuito RL para análisis de respuesta transitoria.
Nuevamente, la clave de este análisis es recordar que la corriente inductora no puede cambiar instantáneamente. Cuando se aplica la energía por primera vez, la corriente circulante debe permanecer en cero. Por lo tanto, no se produce caída de voltaje a través de la resistencia, y por KVL, el voltaje a través del inductor debe ser igual a la fuente,\(E\). Esto establece la tasa inicial de cambio de corriente a través de la Ecuación 9.2.9\((di/dt = E/L)\) y se representa por la línea roja discontinua en la gráfica de la Figura 9.5.2 . A medida que la corriente comienza a aumentar, la caída de voltaje a través de la resistencia comienza a aumentar. Esto reduce el voltaje disponible para el inductor, ralentizando así la tasa de cambio de corriente. Esto es representado por la curva roja sólida en la gráfica. Mientras tanto, la curva azul sólida representa el voltaje decreciente del inductor. Así, en el circuito RL, la curva de voltaje del inductor hace eco de la curva de corriente del circuito RC (o curva de voltaje de resistencia), y la curva de corriente RL hace eco de la curva de voltaje del condensador del circuito RC.
Las curvas presentadas en la Figura 9.5.2 son idénticas a las presentadas en el Capítulo 8 cuando discutimos los capacitores. Se reproducen aquí para su conveniencia.
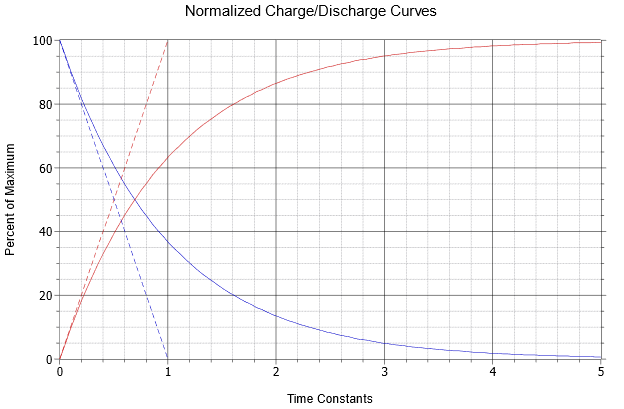
Figura 9.5.2 : Curvas normalizadas de carga y descarga.
Como se señaló anteriormente, la tasa de cambio actual versus tiempo es igual a\(\mathcal{v}/L\), y por lo tanto en este caso,\(E/L\). Si la tasa inicial de cambio continuara sin disminuir, la corriente máxima (de estado estacionario),\(E/R\), se alcanzaría en\(L/R\) segundos 1. Por lo tanto, la constante de tiempo para un circuito RL es:
\[\tau = \frac{L}{R} \label{9.13} \]
Una vez más, cinco constantes lograrán el estado estacionario.
Siguiendo el trabajo previo sobre capacitores, las ecuaciones relevantes para el circuito RL se pueden mostrar como 2:
\[V_L (t) = E \epsilon^{− \frac{t}{\tau}} \label{9.14} \]
\[V_R (t) = E \left(1 − \epsilon^{− \frac{t}{\tau}} \right) \label{9.15} \]
\[I (t) = \frac{E}{R} \left(1 − \epsilon^{− \frac{t}{\tau}} \right) \label{9.16} \]
Dónde
\(V_L(t)\)es el voltaje del inductor en el momento\(t\),
\(V_R(t)\)es el voltaje del resistor en el momento\(t\),
\(I(t)\)es la corriente en el momento\(t\),
\(E\)es el voltaje de la fuente,
\(R\)es la resistencia en serie,
\(t\)es el momento de interés,
\(\tau\)es la constante de tiempo,
\(\varepsilon\)(también escrito\(e\)) es la base de logaritmos naturales, aproximadamente 2.718.
Tiempo para un ejemplo.
Dado el circuito de la Figura 9.5.3 , supongamos que el switch está cerrado en el momento\(t = 0\). Determine la constante de tiempo de carga, la cantidad de tiempo después de que el interruptor se cierre antes de que el circuito alcance el estado estacionario, y el voltaje y la corriente del inductor a\(t = 0\),\(t = 2\) microsegundos y\(t = 1\) milisegundos. Supongamos que el inductor está inicialmente descargado.
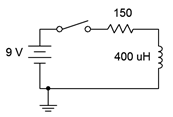
Figura 9.5.3 : Circuito por ejemplo 9.5.1 .
Primero, la constante de tiempo:
\[\tau = \frac{L}{R} \nonumber \]
\[\tau = \frac{400 \mu H}{150 \Omega} \nonumber \]
\[\tau \approx 2.667 \mu s \nonumber \]
El estado estacionario se alcanzará en cinco constantes de tiempo, o aproximadamente 13.33 microsegundos. Así sabemos que\(V_L(0) = 9\) voltios y\(V_L(1 ms) = 0\) voltios. Debido a que el inductor es un abierto inicialmente,\(I_L(0) = 0\) amperios. A\(I_L\) (1 ms), el circuito está en estado estacionario y el inductor actúa como un corto. Por lo tanto, toda la fuente de 9 voltios cae a través de la\(\Omega\) resistencia 150, para 60 mA.
Para encontrar\(V_L\) (2\ mu s) simplemente resolvemos la Ecuación\ ref {9.14}.
\[V_L (t) = E \epsilon^{− \frac{t}{\tau}} \nonumber \]
\[V_L (2 \mu s) = 9V \epsilon^{− \frac{2 \mu s}{2.667 \mu s}} \nonumber \]
\[V_L (2 \mu s) \approx 4.251 V \nonumber \]
Este valor también se puede determinar gráficamente a partir de la Figura 9.5.2 . El tiempo de 2 microsegundos representa 75% de una constante de tiempo. Encuentre este valor en el eje horizontal y luego siga recto hasta la curva azul sólida que representa el voltaje del inductor de carga. El punto de intersección es justo alrededor del 47% del valor máximo en el eje vertical. El valor máximo aquí es el voltaje de fuente de 9 voltios. Por lo tanto, el inductor habrá alcanzado aproximadamente 47% de 9 voltios, o poco más de 4.2 voltios.
La corriente se puede encontrar de manera similar usando la Ecuación\ ref {9.16}.
\[I_L (t) = \frac{E}{R} \left(1 − \epsilon^{− \frac{t}{\tau}} \right) \nonumber \]
\[I_L (2 \mu s) = \frac{9V}{150 \Omega} \left( 1 − \epsilon^{− \frac{2 \mu s}{2.667 \mu s}} \right) \nonumber \]
\[I_L (2 \mu s) = 60mA \left( 1 − \epsilon^{−0.75} \right) \nonumber \]
\[I_L (2 \mu s) = 31.66mA \nonumber \]
Simulación por Computadora
Para verificar nuestro análisis, el circuito de la Figura 9.5.3 se introduce en un simulador, como se muestra en la Figura 9.5.4 . Para reflejar la noción de un circuito variable en el tiempo con un interruptor, la fuente de voltaje de CC de 9 voltios ha sido reemplazada por una fuente de voltaje de pulso rectangular. Esta fuente arranca a 0 voltios y luego inmediatamente aumenta hasta 9 voltios. Permanece en este nivel durante 20 microsegundos antes de volver a caer a 0 voltios.
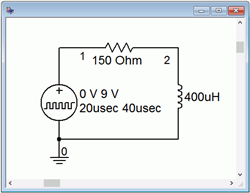
Figura 9.5.4 : El circuito de la Figura 9.5.3 en un simulador.
Los resultados de un análisis transitorio se muestran en la Figura 9.5.5 . La forma de onda mostrada rastrea el voltaje del inductor en el nodo 2 con respecto a tierra.
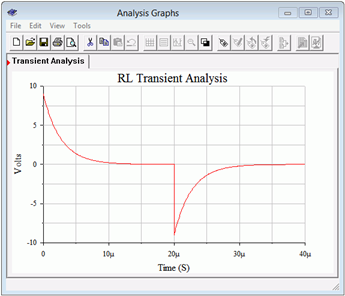
Figura 9.5.5 : Resultados de simulación para el circuito de la Figura 9.5.3 .
Podemos ver que el voltaje inicia en 9 voltios como se esperaba. Luego vuelve a caer a cero y se encuentra en estado estacionario en menos de 15 microsegundos, tal como se predijo. A los 20 microsegundos, la fuente de pulso vuelve a cero voltios. En este instante, la corriente a través del inductor debe seguir siendo la corriente de estado estacionario de 60 miliamperios. Esta corriente seguirá fluyendo en el sentido de las agujas del reloj, por lo que producirá una caída de 9 voltios a través de la\(\Omega\) resistencia 150 con una polaridad de + a − de izquierda a derecha. Esto efectivamente coloca al nodo 2 negativo con respecto al suelo. El resultado es que la polaridad del voltaje del inductor se voltea, con el inductor ahora actuando como una fuente de corta duración. Esto lo vemos en el análisis transitorio como un pico negativo de 9 voltios. La constante de tiempo de descarga es idéntica a la constante de carga, y así vemos que el voltaje del inductor vuelve a caer a cero en la misma cantidad de tiempo.
Dado el circuito de la Figura 9.5.6 , encuentra\(V_L\) en\(t = 1\) microsegundos después de que el circuito esté energizado. Supongamos que el inductor está inicialmente descargado.
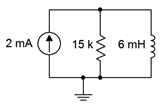
Figura 9.5.6 : Circuito por ejemplo 9.5.2 .
Primero, la constante de tiempo:
\[\tau = \frac{L}{R} \nonumber \]
\[\tau = \frac{6 mH}{15 k\Omega} \nonumber \]
\[\tau = 400 ns \nonumber \]
El estado estacionario se alcanzará en cinco constantes de tiempo, o 2 microsegundos, momento en el que el voltaje del inductor será cero ya que se comportará como un corto. En contraste, como el inductor es inicialmente abierto\((I_L(0) = 0)\), toda la corriente de la fuente fluirá hacia la\(\Omega\) resistencia de 15 k, produciendo 30 voltios a través de esta red paralela. Por lo tanto, podemos afirmar que\(V_L(0) = 30\) voltios y\(V_L\) (2\ mu s) = 0 voltios, definiendo los extremos. Para encontrar\(V_L\) (1\ mu s), podemos usar la Ecuación\ ref {9.14}.
\[V_L (t) = E \epsilon^{− \frac{t}{\tau}} \nonumber \]
\[V_L (1 \mu s) = 30 V \epsilon^{− \frac{1 \mu s}{0.4 \mu s}} \nonumber \]
\[V_L (1 \mu s) \approx 2.463 V \nonumber \]
Hay algunas formas diferentes de realizar una comprobación cruzada de este valor. Para empezar, podemos determinar la corriente del inductor usando una ligera modificación de la Ecuación\ ref {9.16} (el valor de la fuente de corriente se usa en lugar de\(E/R\) ya que la ecuación requiere efectivamente la corriente máxima o de estado estacionario).
\[I_L (t) = I \left( 1 − \epsilon^{− \frac{t}{\tau}} \right) \nonumber \]
\[I_L (1 \mu s) = 2mA \left( 1 − \epsilon^{− \frac{1 \mu s}{0.4 \mu s}} \right) \nonumber \]
\[I_L (1 \mu s) = 1.836mA \nonumber \]
El voltaje inductor de 2.463 voltios también tendría que aparecer a través de la\(\Omega\) resistencia paralela de 15 k. Esto produce 2.463 V/15 k\(\Omega\), o 0.164 mA de corriente de resistencia. Por KCL, el resto de la corriente de fuente de 2 mA debe fluir hacia abajo a través del inductor. Esto produce una corriente neta de inductor de 2 mA − 0.164 mA, o 1.836 mA, verificando nuestro resultado anterior.
Ejemplo 9.5.2 también refuerza el concepto de que la constante de tiempo es inversamente proporcional a la resistencia, en lugar de directamente proporcional como en el caso RC. En el circuito de la Figura 9.5.6 , debería ser obvio que cuanto mayor sea el valor de resistencia, mayor será el voltaje de estado inicial resultante. De la Ecuación 9.2.9 se puede observar que si se incrementa el voltaje a través del inductor, entonces la tasa inicial de cambio de corriente con respecto al tiempo aumentará, y eso implica una constante de tiempo más corta.
Para circuitos más complejos, el teorema de Thévenin puede ser utilizado para determinar el voltaje efectivo de la fuente y la resistencia de carga. Como vimos con los circuitos RC, también es posible que la resistencia de descarga sea considerablemente diferente de la resistencia de carga. En tal caso, las curvas de carga y descarga pueden ser altamente asimétricas tanto en tiempo como en amplitud. Generalmente, cuanto mayor sea la resistencia de descarga cuando se compara con la resistencia de carga, mayor es el voltaje y más corto en el tiempo será el pico de descarga (piense en términos de que el área bajo la curva se mantenga constante).
Supongamos que la corriente inicial a través del inductor es cero en la Figura 9.5.7 . Determinar la constante de tiempo. Además, determine el voltaje del inductor y el voltaje a través de la\(\Omega\) resistencia de 6 k 200 nanosegundos después de que se cierre el interruptor.
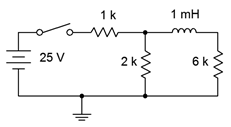
Figura 9.5.7 : Circuito para Ejemplo 9.5.3 .
Este circuito se basa en el circuito presentado en la Figura 9.3.2 como se usa en el Ejemplo 9.3.1. En ese análisis se descubrió que la tensión en estado estacionario para las\(\Omega\) resistencias de 6 k\(\Omega\) y 2 k fue de 15 voltios, estando el par en paralelo. Además, el voltaje inicial a través de la\(\Omega\) resistencia de 2 k y el inductor fue de 16.67 voltios y para la\(\Omega\) resistencia de 6 k, 0 voltios.
Para el circuito Thévenin, el voltaje de circuito abierto en el inductor sería el potencial a través de la\(\Omega\) resistencia de 2 k, que se obtiene de un divisor de voltaje entre éste y la\(\Omega\) resistencia de 1 k, o 16.67 voltios. La resistencia equivalente se obtiene cortocircuitando la fuente de voltaje que deja las\(\Omega\) resistencias de 1 k\(\Omega\) y 2 k en paralelo, que luego se encuentra en serie con la\(\Omega\) resistencia de 6 k, produciendo aproximadamente 6.667 k\(\Omega\). El equivalente se muestra en la Figura 9.5.8 .
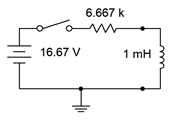
Figura 9.5.8 : Thévenin equivalente del circuito de la Figura 9.5.7 accionando el inductor.
De inmediato, podemos ver que el voltaje de estado inicial a través del inductor se confirma en el circuito equivalente. Ahora podemos determinar la constante de tiempo.
\[\tau = \frac{L}{R} \nonumber \]
\[\tau = \frac{1mH}{6.667 k \Omega} \nonumber \]
\[\tau = 150 ns \nonumber \]
El estado estacionario se alcanzará en 750 nanosegundos. Para encontrar el voltaje del inductor podemos usar la Ecuación\ ref {9.14}.
\[V_L (t) = E \epsilon^{− \frac{t}{\tau}} \nonumber \]
\[V_L (200 ns) = 16.67V \epsilon^{− \frac{200 ns}{150 ns}} \nonumber \]
\[V_L (200 ns) \approx 4.39 V \nonumber \]
Refiriéndose de nuevo al circuito original, para determinar el voltaje a través de la\(\Omega\) resistencia de 6 k podemos encontrar la corriente a través de él y usar la ley de Ohm. La corriente sería la misma que la corriente del inductor ya que las dos están en serie. Así, la Ecuación\ ref {9.16} haría el truco.
\[I_L (t) = \frac{E}{R} \left( 1 − \epsilon^{− \frac{t}{\tau}} \right) \nonumber \]
\[I_L (200 ns) = \frac{16.67V}{6.667 k \Omega} \left( 1 − \epsilon^{− \frac{200 ns}{150 ns}} \right) \nonumber \]
\[I_L (200 ns) = 2.5mA \left( 1 − \epsilon^{−1.333} \right) \nonumber \]
\[I_L (200 ns) \approx 1.841mA \nonumber \]
Y finalmente,
\[V_{6k} (200 ns) = I R \nonumber \]
\[V_{6k} (200 ns) = 1.841 mA 6 k \Omega \nonumber \]
\[V_{6k} (200 ns) \approx 11.05 V \nonumber \]
Además, el voltaje a través de la\(\Omega\) resistencia de 2 k debe ser la suma, o aproximadamente 15.44 voltios.
Simulación por Computadora
Los resultados de Example 9.5.3 son verificados en un simulador. Una vez más el circuito se construye usando un generador de pulsos, como se muestra en la Figura 9.5.9 .
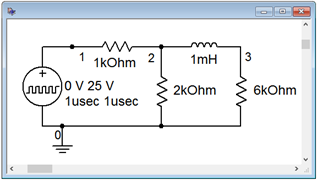
Figura 9.5.9 : Circuito de la Figura 9.5.7 en un simulador.
Se realiza un análisis transitorio a 1 microsegundo que se encuentra modestamente en estado estacionario. Se representan los voltajes de nodo 2 y 3, como se muestra en la Figura 9.5.10 . El voltaje inicial a través de la\(\Omega\) resistencia de 2 k (nodo 2) es como se predijo, aproximadamente 16.7 voltios, y cae a 15 voltios en estado estacionario, aproximadamente 750 nanosegundos después. El voltaje a través de la\(\Omega\) resistencia de 6 k (nodo 2) comienza en cero voltios y también termina a 15 voltios en estado estacionario, tal como se predijo. Además, tenga en cuenta que se verifican los voltajes predichos a través de las\(\Omega\) resistencias de 2 k\(\Omega\) y 6 k a 200 nanosegundos.
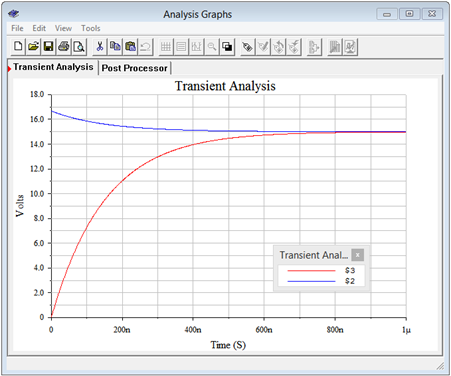
Figura 9.5.10 : Simulación de análisis transitorio del circuito de la Figura 9.5.7 .
El voltaje a través del inductor es el nodo 2 menos el nodo 3. Este diferencial se traza por separado en la Figura 9.5.11 . Los voltajes esperados iniciales, de estado estacionario y de 200 nanosegundos son los predichos.
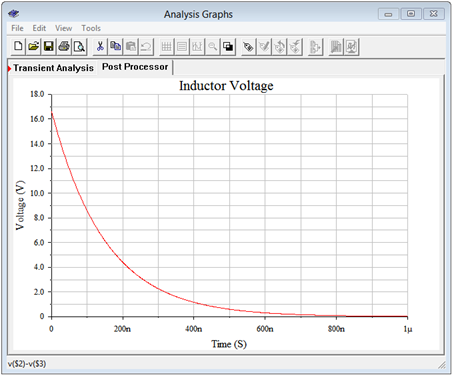
Figura 9.5.11 : Simulación del voltaje del inductor frente al tiempo para el circuito de la Figura 9.5.7 .
Una observación muy importante es que si un circuito RL es alterado o abierto abruptamente, pueden ocurrir picos de voltaje muy grandes. Esto se debe a que la corriente del inductor no puede cambiar instantáneamente. Si el circuito está abierto, el abierto representa una resistencia muy grande. La ley de Ohm indica que la corriente del inductor multiplicada por esta resistencia muy grande puede producir un voltaje muy grande a través del nuevo abierto. De hecho, el potencial puede ser suficiente para provocar una chispa o arco. Tenga en cuenta que debido a que la corriente no puede cambiar instantáneamente (tanto de magnitud como de dirección), el inductor ahora se comporta como una fuente de voltaje de muy alta magnitud y con polaridad inversa. Este fenómeno se utiliza para crear la chispa de encendido en motores de combustión interna. En definitiva, la bobina de encendido está cargada, creando cierto flujo de corriente. Luego se interrumpe el circuito dejando solo la bobina en serie con la bujía, siendo la bujía poco más que un espacio de tamaño preciso entre dos electrodos. Esto da como resultado que se desarrolle un voltaje grande a través de la brecha de la bujía, típicamente en la vecindad de 20,000 voltios, que es suficiente para crear un pequeño arco (es decir, la chispa) que luego enciende la mezcla de aire-combustible en el pistón.
Un ejemplo de producción de un pico de voltaje de descarga que es considerablemente mayor que el voltaje de la fuente se puede ilustrar con el circuito de la Figura 9.5.12 . Supondremos que el inductor está inicialmente descargado cuando se aplica potencia, y que el interruptor se encuentra en la posición 1. En este caso, el circuito consiste solo en la fuente de 12 voltios, la\(\Omega\) resistencia de 2.2 k y el inductor. El circuito alcanza el estado estacionario en aproximadamente 227 nanosegundos. En ese punto el inductor se comporta como un cortocircuito, dejando que la fuente completa de 12 voltios caiga a través de la\(\Omega\) resistencia de 2.2 k. Esto produce una corriente en sentido horario de aproximadamente 5.455 mA.
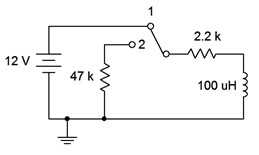
Figura 9.5.12 : Circuito que ilustra un pico de voltaje de descarga grande.
Si ahora movemos el interruptor a la posición 2, esta corriente debe mantenerse porque la corriente a través del inductor no puede cambiar instantáneamente. La nueva resistencia de descarga es ahora la combinación en serie de las dos resistencias, o 49.2 k\(\Omega\). La ley de Ohm y KVL dictan que el voltaje del inductor resultante debe ser 49.2 k\(\Omega\) por 5.455 mA, o justo más allá de −268 voltios. Este potencial es negativo porque la corriente en sentido horario fluye hacia arriba a través de la\(\Omega\) resistencia de 47 k, produciendo una caída + a − desde tierra hacia arriba. El aumento de la resistencia también acorta la constante de tiempo y ahora el estado estacionario se alcanzará en solo 10.1 nanosegundos. Así, vemos un pico de magnitud mucho mayor (más de veinte veces el de la tensión de la fuente) con una duración de tiempo mucho más corta (menos de una vigésima parte del tiempo de carga).
Dependiendo del tipo de interruptor que se utilice, las cosas pueden ser incluso más extremas de lo que se acaba de describir. Los interruptores vienen en dos variedades básicas: make-before break y break-fore-make. El primero hace contacto con la segunda posición antes de que rompa el contacto con la primera posición, mientras que el segundo hace lo contrario. El comportamiento que se acaba de describir supone que se está utilizando un interruptor de hacer antes de romper. Por el contrario, si se usa un interruptor de interrupción antes de hacer, veríamos un resultado drásticamente diferente.
Volvamos a recoger en estado estacionario con 5.455 mA fluyendo a través del inductor. Ahora lanzamos el interruptor a la posición 2. Este nuevo interruptor rompe el contacto con el cable que conduce de nuevo a la fuente de voltaje antes de que haga contacto con la\(\Omega\) resistencia de 47 k. Por un corto instante de tiempo el interruptor no está haciendo contacto con nada y la resistencia resultante en el bucle está determinada por el entrehierro entre los contactos del interruptor. Incluso si esto fuera un mero 10 M\(\Omega\), el potencial resultante sería de más de 50,000 voltios. Esto seguramente creará una chispa y habremos recreado inadvertidamente el escenario de la bujía. Ojalá no haya gases combustibles cerca.
Referencias
1 Es decir,\(E/L\) amperios por segundo veces\(L/R\) segundos produce\(E/R\) amperios.
2 Véase también el Apéndice C.


