10.6: Ejercicios

Última actualización
Guardar como PDF

Page ID: 86108

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Análisis

1. En el circuito magnético mostrado en la Figura 10.6.1 , supongamos que la sección transversal es de 1 cm por 1 cm con una longitud de trayectoria de 8 cm. Todo el núcleo está hecho de chapa de acero y hay 100 vueltas en el devanado. Determine la corriente para establecer un flujo de 8E−5 webers.

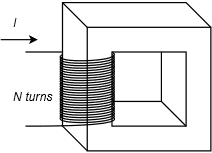
Figura 10.6.1

2. Repita el problema 1 usando acero fundido para el núcleo.

3. Dado el núcleo mostrado en la Figura 10.6.1 , supongamos que la sección transversal es de 2 cm por 2 cm con una longitud de trayectoria de 10 cm. Todo el núcleo está hecho de acero fundido y hay 200 vueltas en el devanado. Determine la corriente para establecer un flujo de 4E−4 webers.

4. Repita el problema 3 usando chapa de acero para el núcleo.

5. En el circuito magnético mostrado en la Figura 10.6.1 , supongamos que la sección transversal es de 1 cm por 1 cm con una longitud de trayectoria de 8 cm. Todo el núcleo está hecho de chapa de acero. Determine el número de vueltas necesarias para establecer un flujo de 8E−5 webers dada una corriente de 50 mA.

6. Dado el núcleo mostrado en la Figura 10.6.1 , supongamos que la sección transversal es de 2 cm por 2 cm con una longitud de trayectoria de 10 cm. Todo el núcleo está hecho de chapa de acero Determine el número de vueltas requeridas para establecer un flujo de 4E−4 webers dada una corriente de 200 mA.

7. En el circuito magnético mostrado en la Figura 10.6.2 , supongamos que la sección transversal es de 1 cm por 1 cm. La Sección A es de chapa de acero con una longitud de trayectoria de 6 cm. La Sección B es de acero fundido con una longitud de 2 cm. Hay 500 vueltas en el devanado. Determine la corriente para establecer un flujo de 5E−5 webers.

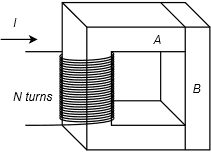
Figura 10.6.2

8. En el circuito magnético mostrado en la Figura 10.6.2 , supongamos que la sección transversal es de 1 cm por 1 cm. La Sección A es de chapa de acero con una longitud de trayectoria de 6 cm. La Sección B es de acero fundido con una longitud de 2 cm. Determine el número de vueltas en la bobina para establecer un flujo de 6E−5 webers con una corriente de 50 mA.

9. Un transformador se muestra en la Figura 10.6.3 , supongamos que la sección transversal es de 5 cm por 5 cm. El núcleo es de chapa de acero con una longitud de trayectoria de 20 cm. \(N1\)es de 500 vueltas y\(N2\) es de 200 vueltas. Determine la corriente secundaria\((I2)\) si una corriente primaria\((I1)\) de 1 amperio establece un flujo de 1.5E−3 webers.

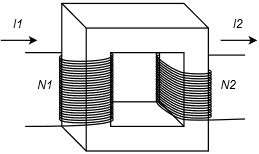
Figura 10.6.3

10. Dadas las mismas condiciones del problema 9, alterar los giros secundarios\((N2)\) para que la corriente secundaria\((I2)\) sea de 3 amperios dada la corriente primaria original de 1 amp.

11. En general, ¿cómo cambiaría el desempeño señalado en el problema 9 si se sustituyera el acero fundido por chapa de acero?

12. Dados los resultados de los problemas del 9 al 11, ¿qué\(N2\) representa la relación de\(N1\) a en términos de rendimiento idealizado y qué pasos se deben tomar para que el transformador funcione lo más cerca posible de lo ideal posible?

13. Dado el circuito magnético mostrado en la Figura 10.6.4 , supongamos que la sección transversal es de 1 cm por 2 cm con una longitud de trayectoria de 6 cm. Todo el núcleo está hecho de chapa de acero con la excepción de un espacio de aire de 1 mm. Determine la corriente requerida para establecer un flujo de 4E−4 webers si\(N = 1000\) gira.

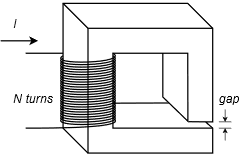
Figura 10.6.4

14. Utilizando los datos dados en el problema 13, determinar el número de vueltas requeridas para establecer el mismo flujo cuando la corriente de entrada es de 200 mA.

15. Un transformador ideal tiene una relación de reducción de voltaje de 6:1. Si el primario es accionado por 24 VCA y la carga es 100\(\Omega\), determine el voltaje y la corriente de carga, y la corriente del lado primario.

16. Se especifica que un transformador de 120 VCA tiene un secundario con toma central de 36 voltios. Si cada lado del secundario está conectado a su propia\(\Omega\) carga 50, determine las corrientes de carga y la corriente del lado primario.

17. Un transformador ideal tiene una relación reductora de voltaje de 12:1. Si el secundario está conectado a una\(\Omega\) carga 10, ¿qué impedancia se ve desde el lado primario?

18. Un transformador ideal tiene una relación de elevación de voltaje de 1:5. Si el secundario está conectado a una\(\Omega\) carga 2, ¿qué impedancia se ve desde el lado primario?

Diseño

19. Un transformador reductor\(N=8\) tiene un secundario RMS de 15 voltios que está conectado a una carga con un valor efectivo de 5\(\Omega\). Determinar la clasificación VA mínima aceptable del transformador.

20. Un transformador elevador con\(N=.5\) es accionado desde una fuente de 120 VCA. El secundario está conectado a una carga con un valor efectivo de 150\(\Omega\). Determine la clasificación VA mínima aceptable del transformador.

Desafío

21. Un transformador especificado como que tiene un primario de 120 VCA con un secundario de 18 voltios se conecta accidentalmente hacia atrás, con su secundario conectado a la fuente y su primario conectado a una\(\Omega\) carga de 16. Determine la corriente de carga tanto en las conexiones normales como invertidas. También determine la clasificación VA del transformador requerida para ambas conexiones.

22. Considere el sistema de direcciones públicas distribuidas para un aeropuerto como se muestra en la Figura 10.6.5 . Consiste en un amplificador de potencia de audio con una salida RMS nominal de 70 voltios que se conecta a cuatro altavoces remotos, cada uno separado de los demás y a unos 150 metros del amplificador. Cada conjunto de altavoces incluye un transformador reductor de voltaje 10:1 que alimenta la impedancia del altavoz de 8\(\Omega\) (resistiva) de su secundario. Estas cuatro líneas son alimentadas en paralelo por el amplificador. Determine la potencia entregada a cada altavoz y la corriente total entregada por el amplificador de potencia. Supongamos que los transformadores son ideales e ignora cualquier resistencia del cable.

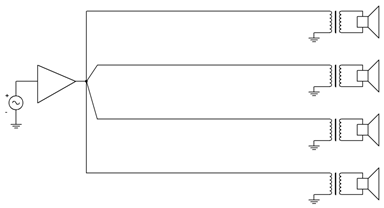
Figura 10.6.5

23. Continuando con el problema anterior, supongamos que el cableado que conecta cada transformador de nuevo al amplificador es AWG 22. Determine la pérdida de energía en cada una de las secciones de cable dual de 150 metros de largo. Además, supongamos que el sistema se reconfigura sin los transformadores y la salida del amplificador se baja a 7 voltios RMS para compensar. Determine la pérdida de energía en cada una de las alimentaciones de cable bajo la nueva configuración.

Simulación

24. Utilizar un análisis transitorio para verificar los resultados del problema 15.

25. Utilizar un análisis transitorio para verificar los resultados del problema 16.