2.4: Modulación analógica

Las formas de onda y los espectros de las señales con métodos comunes de modulación analógica se muestran en la Figura\(\PageIndex{1}\). La señal moduladora se conoce generalmente como la señal de banda base y contiene toda la información a transmitir e interpretar en el receptor. Las formas de onda en la Figura\(\PageIndex{1}\) son estilizadas. Se presentan de esta manera para que los efectos de la modulación se puedan ver más fácilmente. La señal de banda base (Figura\(\PageIndex{1}\) (a)) se muestra como teniendo un periodo que no es mucho mayor que el periodo de la portadora (Figura\(\PageIndex{1}\) (b)). En realidad habría cientos o miles de ciclos de RF por cada ciclo de la señal de banda base de manera que el componente de frecuencia más alta de la señal de banda base sea una pequeña fracción de la frecuencia portadora. En esta situación, los espectros mostrados a la derecha en la Figura\(\PageIndex{1}\) (c—e) serían demasiado estrechos para permitir ver cualquier detalle.

2.4.1 Modulación de Amplitud

La modulación de amplitud (AM) es el método de modulación analógica más simple de implementar. Aquí se utiliza una señal para variar lentamente la amplitud de la portadora según el nivel de la señal moduladora. Con AM (Figura\(\PageIndex{1}\) (c)) se modula la amplitud de la portadora, y esto da como resultado una ampliación del espectro de la portadora, como se muestra en la Figura\(\PageIndex{1}\) (c) (ii). Este espectro contiene el componente portador original y las bandas laterales superior e inferior, designadas como U y L, respectivamente. En AM, las dos bandas laterales contienen información idéntica, por lo que toda la información contenida en la señal de banda base se transmite si solo se transmite una banda lateral.

La señal AM básica\(x(t)\) tiene la forma

\[\label{eq:1}x(t)=A_{c}\left[1+my(t)\right]\cos (2\pi f_{c}t) \]

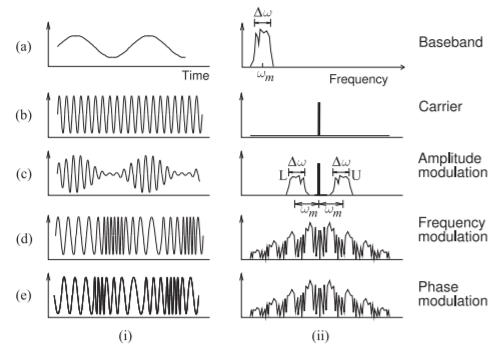
Figura\(\PageIndex{1}\): Modulación analógica básica que muestra la (i) forma de onda y (ii) el espectro para (a) señal de banda base; (b) portadora; (c) portadora modulada mediante modulación de amplitud; (d) portadora modulada mediante modulación de frecuencia; y (e) portadora modulada usando modulación de fase.

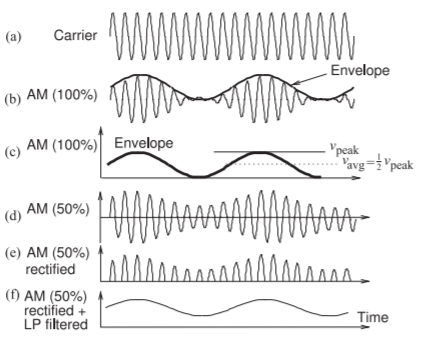
Figura\(\PageIndex{2}\): AM que muestra la relación entre la portadora y la envolvente de modulación: (a) portadora; (b) portadora modulada en\(100\%\) amplitud; (c) señal modulada o de banda base; (d) portadora\(50\%\) modulada en amplitud; (e) señal modulada\(50\%\) AM rectificada; y (f) rectificada y paso bajo (LP) señal\(50\%\) modulada filtrada. La envolvente contiene solo información de amplitud y para AM la envolvente es la misma que la señal de banda base.

donde\(m\) está el índice de modulación,\(y(t)\) es la señal portadora de información de banda base que tiene componentes de frecuencia que son mucho más bajos que la frecuencia portadora\(f_{c}\), y el valor máximo de\(|y(t)|\) es uno. Siempre que\(y(t)\) varíe lentamente en relación con el portador,\(x(t)\) parece un portador cuya amplitud varía lentamente. Para tener una idea de cuán lentamente varía la amplitud en un sistema real, considere una radio AM que transmita en\(1\text{ MHz}\) (que está en medio de la banda de transmisión AM). El componente de frecuencia más alta de la señal moduladora correspondiente a la voz es aproximadamente\(4\text{ kHz}\). Así, la amplitud de la portadora requiere ciclos de\(250\) portadora para pasar por una variación de amplitud completa. En todo momento un ciclo de la portadora modulada, la pseudo-portadora, parece ser periódico, pero de hecho no lo es del todo.

El concepto de la envolvente de una señal de RF modulada se introduce en la Figura\(\PageIndex{2}\). La envolvente es un concepto importante y está directamente relacionada con la distorsión introducida por el hardware analógico y con los requisitos de alimentación de CC que determinan la duración de la batería de las radios móviles. La Figura\(\PageIndex{2}\) (a) es la portadora y la portadora modulada en amplitud se muestra en la Figura\(\PageIndex{2}\) (b). El contorno de la portadora modulada se denomina envolvente, y para AM esto es idéntico a la señal moduladora, es decir, de banda base. El sobre se muestra nuevamente en la Figura\(\PageIndex{2}\) (c). En el pico de la envolvente, la señal de RF tiene una potencia máxima a corto plazo (considerando la potencia de un solo ciclo de RF). Con\(100\%\) AM,\(m = 1\) en Ecuación\(\eqref{eq:1}\), no hay potencia de RF a corto plazo cuando la envolvente está en su mínimo. La señal modulada con\(50\%\) modulación,\(m = 0.5\), se muestra en la Figura\(\PageIndex{2}\) (d) y en todo momento existe una potencia de señal RF apreciable.

Se requiere un hardware analógico muy simple para demodular la señal modulada en amplitud básica, es decir, una señal AM con una portadora y ambas bandas laterales. El receptor requiere filtrado de paso de banda para seleccionar el canal de la señal de radio entrante y luego rectificar la salida del filtro de paso de banda. La forma de onda después de la rectificación de una señal\(50\%\) AM se muestra en la Figura\(\PageIndex{2}\) (e) y contiene componentes de frecuencia en banda base y bandas laterales alrededor de armónicos de la portadora, y los armónicos de la propia portadora. El filtrado de paso bajo de la forma de onda rectificada extrae la señal de banda base original y completa la demodulación, ver Figura\(\PageIndex{2}\) (f). La única electrónica requerida es

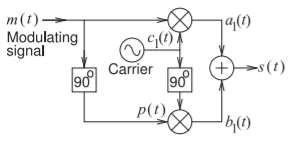
Figura\(\PageIndex{3}\): Modulador Hartley implementando modulación de portadora suprimida de banda única (SSB-SC). Los bloques “\(90^{\circ}\)” desplazan la fase de la señal por\(+90^{\circ}\). El mezclador indicado por el círculo con una cruz es un multiplicador ideal, e.g\(a_{1}(t) = m(t) \cdot c_{1}(t)\).

un solo diodo. La desventaja es que se usa más espectro del requerido y la señal más grande es la portadora que no transmite información pero causa interferencia en otras radios. Sin que se transmitan la portadora y ambas bandas laterales es necesario usar DSP para demodular la señal.

No es posible representar una señal de banda base real de una manera sencilla y emprender las derivaciones analíticas que ilustran las características de la modulación. En cambio, es habitual usar una señal de un tono o de dos tonos, derivar resultados y luego extrapolar los resultados para una señal de banda base de ancho de banda finito. Para una señal de banda base de un solo tono\(y(t) = \cos (\omega_{m}t + \phi )\), entonces la señal modulada AM básica, de la ecuación\(\eqref{eq:1}\), es

\[\begin{align}x(t)&=\left[1+m\cos (\omega_{m}t+\phi )\right]\cos (\omega_{c}t)\nonumber \\ \label{eq:2}&=\cos (\omega_{c}t)+\frac{1}{2}m\left[\cos ((\omega_{c}-\omega_{m})t-\phi)+\cos ((\omega_{c}+\omega_{m})t+\phi )\right]\end{align} \]

que tiene tres componentes de frecuencia (radián), uno en la frecuencia portadora\(\omega_{c}\), uno justo debajo de la portadora en\(\omega_{c}-\omega_{m}\), y uno justo arriba en\(\omega_{c} +\omega_{M}\) (desde\(\omega_{m} ≪ \omega_{c}\)). La extensión a una señal de banda base de ancho de banda finito, ver Figura\(\PageIndex{1}\) (a) (ii), es imaginar que ωm va desde un valor más bajo\(\omega_{m}− \frac{1}{2}\Delta\omega\) a un valor más alto\(\omega_{m}+ \frac{1}{2}\Delta\omega\). Los tonos discretos en la señal modulada por debajo y por encima de la portadora se convierten entonces en bandas laterales de ancho de banda finito con una banda lateral inferior L centrada en\(\omega_{c} −\omega_{m}\) y una banda lateral superior U centrada en\((\omega_{c} +\omega_{m})\) cada una teniendo el mismo ancho de banda\(\Delta\omega\), como la señal de banda base, ver Figura\(\PageIndex{1}\) (c) (ii).

El modulador AM descrito hasta ahora produce una señal modulada con una portadora y dos bandas laterales. Esta modulación se llama modulación de doble banda lateral (DSB). Hay información idéntica en cada una de las bandas laterales y por lo tanto solo se necesita transmitir una de las bandas laterales. La portadora no contiene información, por lo que si solo se transmitió una banda lateral, entonces la señal SC de portadora suprimida de banda lateral única (SSB) recibida (junto SSB-SC) tiene toda la información necesaria para recuperar la señal de banda base original. Sin embargo, el simple proceso de demodulación mediante rectificación como se describió anteriormente en esta sección ya no funciona. El receptor necesita usar DSP pero el espectro se usa de manera eficiente.

Un circuito que implementa SSB-SC AM es el modulador Hartley que se muestra en la Figura\(\PageIndex{3}\). Como se verá, esta arquitectura básica es significativa y se utiliza en todas las radios modernas. En las radios modernas el modulador Hartley, o una variante, toma una señal modulada la cual se centra a una frecuencia intermedia y la desplaza hacia arriba en frecuencia para que quede centrada en otra frecuencia un poco por debajo o un poco por encima de la portadora del modulador Hartley.

En un modulador Hartley tanto la señal\(m(t)\) moduladora como la portadora se multiplican juntas en un mezclador y luego también se mezclan versiones con\(90^{\circ}\) desplazamiento de fase antes de ser sumadas juntas. El flujo de la señal es el siguiente comenzando con\(m(t) = \cos (\omega_{m}t +\phi),\: p(t) = \cos (\omega_{m}t + \phi − π/2) = \sin (\omega_{m}t + \phi)\) y la señal portadora\(c_{1}(t)=\cos(\omega_{c}t)\):

\[\begin{align}a_{1}(t)&=\cos (\omega_{m}t+\phi )\cos (\omega_{c}t)=\frac{1}{2}\left[\cos ((\omega_{c}-\omega_{m})t-\phi )+\cos ((\omega_{c}+\omega_{m})t+\phi )\right]\nonumber \\ b_{1}(t)&=\sin (\omega_{m}t+\phi )\sin (\omega_{c}t)=\frac{1}{2}\left[\cos ((\omega_{c}-\omega_{m})t-\phi )-\cos ((\omega_{c}+\omega_{m})t+\phi )\right]\nonumber \\ \label{eq:3} s(t)&=a_{1}(t)+b_{1}(t)=\cos ((\omega_{c}-\omega_{m})t-\phi )\end{align} \]

y así se selecciona la banda lateral inferior (LSB). Una observación interesante es que la fase,\(\phi\), de la señal de banda base también se traduce hacia arriba en frecuencia. Una característica que no se explota en AM sino que está en la modulación digital.

2.4.2 Modulación de fase

En la modulación de fase (PM) la fase de la portadora depende del nivel instantáneo de la señal de banda base. La portadora modulada en fase se muestra en la Figura\(\PageIndex{1}\) (e) (i) y parece que la frecuencia de la portadora modulada está cambiando. Lo que realmente está sucediendo es que cuando la fase está cambiando más rápidamente la frecuencia aparente de la forma de onda de RF cambia. Aquí, a medida que la señal de banda base está disminuyendo, el desplazamiento de fase se reduce y el efecto es aumentar la frecuencia aparente de la señal de RF. A medida que aumenta la señal de banda base, el efecto es reducir la frecuencia aparente de la señal de RF modulada. El resultado es que con PM es que el ancho de banda de la señal variable en el tiempo se dispersa, como se ve en la Figura\(\PageIndex{4}\). PM se puede implementar usando un bucle de bloqueo de fase (PLL) pero aquí se omitirán más detalles.

Considere una señal modulada en fase\(s(t) = \cos(\omega_{c}t+\phi (t))\) donde\(\phi (t)\) está la señal de banda base que contiene la información a transmitir. El espectro de se\(s(t)\) puede determinar simplificando\(\phi (t)\) como una sinusoide con frecuencia\(f_{m} = 2π\omega_{m}\) para que\(\phi (t) =\beta \cos(\omega_{m}t)\) donde\(\beta\) esté el índice de modulación de fase. (El cambio de fase máximo posible es\(±\pi\) y luego\(\beta=\pi\).) La señal modulada en fase se convierte

\[\begin{align}s(t)&=\cos (\omega_{c}t+\beta\cos(\omega_{m}t)])\nonumber \\ \label{eq:4}&=\cos(\omega_{c}t)\cos(\cos(\beta\omega_{m}t))-\sin(\omega_{c}t)\sin(\cos(\beta\omega_{m}t))\end{align} \]

que tiene la expansión basada en la función de Bessel

\[\begin{align} &s(t)=J_{0}(\beta )\cos (\omega_{c}t) \nonumber \\ &+J_{1}(\beta )\cos (\omega_{c}+\omega_{m})t+\pi /2)+J_{1}(\beta)\cos (\omega_{c}-\omega_{m})t+\pi /2)\nonumber \\ &+J_{2}(\beta )\cos (\omega_{c}+2\omega_{m})t+\pi )+J_{2}(\beta )\cos (\omega_{c}-2\omega_{m})t+\pi ]\nonumber \\ \label{eq:5}&+J_{3}(\beta )\cos (\omega_{c}+3\omega_{m})t+3\pi /2)+J_{3}(\beta )\cos (\omega_{c}-3\omega_{m})t+3\pi /2)+\ldots\end{align} \]

donde\(J_{n}\) está la función Bessel del primer tipo de orden\(n\). El espectro de esta señal se muestra en la Figura\(\PageIndex{4}\) (a) que consiste en tonos discretos agrupados como conjuntos de banda lateral inferior y superior centrados en la portadora en\(f_{c}\). Los tonos discretos en las bandas laterales están separados entre sí y de\(f_{c}\) por\(f_{m}\). Las bandas laterales tienen menor amplitud más lejos del portador.

Si la señal moduladora tiene un ancho de banda finito, aproximado\(f_{m}\) variando desde un valor mínimo,\((f_{m} −\Delta f)\) hasta la frecuencia máxima\((f_{m} +\Delta f)\), entonces el espectro de la señal modulada se convierte en el mostrado en la Figura\(\PageIndex{4}\) (b), con los centros de bandas laterales adyacentes separados por\(f_{m}\) y las primeras bandas laterales separadas del portador por fm también. Esto es DSB

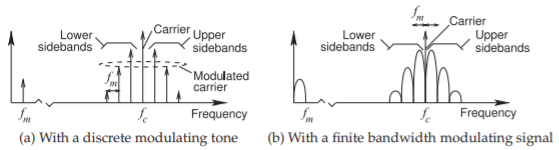
Figura\(\PageIndex{4}\): Espectro de una portadora modulada en fase que incluye la portadora en\(f_{c}\) y bandas laterales superior e inferior con el espectro de la señal moduladora discreta en\(f_{m}\).

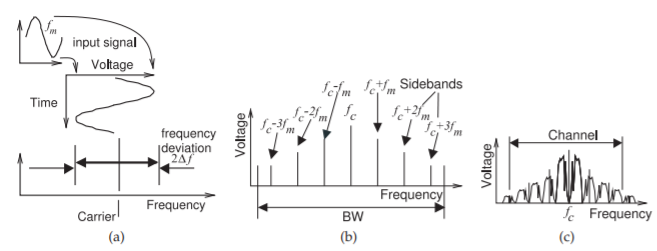
Figura\(\PageIndex{5}\): Modulación de frecuencia: (a) señal de banda base sinusoidal mostrada variando la frecuencia de la portadora y así modulando FM la portadora; (b) el espectro de la forma de onda modulada FM resultante; y (c) espectro de la portadora modulada cuando es modulada por una señal de banda base de banda ancha tal como voz .

modulación y hay una portadora (por lo que no se suprime). Las bandas laterales no llevan información idéntica y se requieren varias, quizás tres por debajo y tres por encima de la portadora, para permitir la demodulación de una señal PM. Por lo tanto, se requiere un ancho de banda bastante grande para transmitir la señal modulada.

2.4.3 Modulación de frecuencia

Los otros esquemas de modulación analógica comúnmente utilizados es la modulación de frecuencia (FM), ver Figura\(\PageIndex{1}\) (d). Las señales producidas por FM y PM parecen ser similares; la diferencia está en cómo se generan las señales. En FM, la amplitud de la señal de banda base determina la frecuencia de la portadora modulada. Considere la forma de onda FM en la Figura\(\PageIndex{1}\) (d) (i). Cuando la señal de banda base está en su valor máximo, la portadora modulada está en su frecuencia mínima, y cuando la señal está en su valor más bajo, la portadora modulada está en su frecuencia máxima. (Dependiendo de la implementación del hardware, podría ser al revés). El resultado es que el ancho de banda de la señal variable en el tiempo se extiende, como se ve en la Figura\(\PageIndex{5}\).

Una forma de implementar el modulador FM es usar un oscilador controlado por voltaje (VCO) con la señal de banda base controlando la frecuencia de un oscilador. Un receptor FM debe comprimir, en frecuencia, la señal transmitida para recrear la señal original de banda base de ancho de banda más estrecha. La demodulación FM puede considerarse como una mejora de señal o una supresión de ruido equivalente en un proceso que se puede llamar ganancia de procesamiento analógico. Solo los componentes de las señales FM originales se colapsan coherentemente a una señal de banda base de ancho de banda más estrecho, mientras que el ruido, al no estar correlacionado, todavía está extendido (aunque reorganizado). Por lo tanto, la relación de las potencias de señal a ruido aumenta, ya que después de la demodulación solo es importante la potencia del ruido en el ancho de banda más pequeño de la señal de banda base. Por lo tanto, en comparación con AM, FM aumenta significativamente la tolerancia al ruido que se puede agregar a la señal durante la transmisión. PM tiene la misma propiedad, aunque los detalles de modulación y demodulación son diferentes. Tanto para las señales de FM como de PM la amplitud máxima del fasor de RF es igual a la amplitud promedio, y así el PMEPR es\(1\) o\(0\text{ dB}\).

Considere una señal de FM\(s(t) = \cos([\omega_{c} + x(t)]t)\) donde\(x(t)\) está la señal de banda base que contiene la información a transmitir. El espectro de se\(s(t)\) puede determinar simplificando\(x(t)\) como una sinusoide con frecuencia\(f_{m} = 2π\omega_{m}\) para que\(x(t) = \beta\cos(\omega_{m}t)\) donde\(\beta\) esté el índice de modulación de frecuencia. La señal FM se convierte

\[\begin{align}s(t)&=\cos([\omega_{c}+\beta\cos(\omega_{m}t)]t)\nonumber \\ \label{eq:6}&=\cos(\omega_{c}t)\cos(\cos(\omega_{m}t)\beta t)-\sin(\omega_{c}t)\sin(\cos(\omega_{m}t)\beta t)\end{align} \]

que tiene la expansión basada en la función de Bessel

\[\begin{align}&s(t)=J_{0}(\beta t)\cos (\omega_{c}t)\nonumber \\&-J_{1}(\beta )\sin(\omega_{c}+\omega_{m})t+\pi /2)-J_{1}(\beta t)\sin(\omega_{c}-\omega_{m})t+\pi /2)\nonumber \\ &-J_{2}(\beta t)\cos(\omega_{c}-2\omega_{m})t+\pi )+K_{2}(\beta t)\cos (\omega_{c}-2\omega_{m})t+\pi ]\nonumber \\ \label{eq:7}&+J_{3}(\beta t)\sin(\omega_{c}+3\omega_{m})t+3\pi /2)+J_{3}(\beta t)\sin(\omega_{c}-3\omega_{m})t+3\pi /2)+\ldots\end{align} \]

donde\(J_{n}\) está la función Bessel del primer tipo de orden\(n\). El espectro de esta señal se muestra en la Figura\(\PageIndex{5}\) (b) que consiste en tonos discretos agrupados como conjuntos de banda lateral inferior y superior centrados en la portadora en\(f_{c}\). Los tonos discretos en las bandas laterales están separados entre sí y de\(f_{c}\) por\(f_{m}\). Las bandas laterales tienen menor amplitud más lejos del portador.

Si la señal moduladora tiene un ancho de banda finito, aproximado\(f_{m} = \omega_{m}/(2π)\) variando desde un valor mínimo (\(f_{m}− \Delta f)\)hasta la frecuencia máxima\((f_{m}+\Delta f)\), entonces el espectro de la señal modulada se convierte en el mostrado en la Figura\(\PageIndex{5}\) (c) con los centros de bandas laterales adyacentes separados por\(f_{m}\) y las primeras bandas laterales del portador por\(f_{m}\) también. Esta es la modulación DSB y hay una portadora (por lo que no se suprime sino que es más pequeña que con AM). Las bandas laterales no llevan información idéntica y se requieren varias, quizás tres a cada lado de la portadora, para permitir la demodulación de una señal FM. Por lo tanto, se requiere un ancho de banda bastante grande para transmitir la señal modulada, ya que no es suficiente transmitir solo una banda lateral para permitir la demodulación.

Regla de Carson

Las señales moduladas en frecuencia y fase tienen un espectro muy amplio y el ancho de banda requerido para transmitir de manera confiable una señal PM o FM es subjetivo. El criterio mejor aceptado para determinar el requisito de ancho de banda se llama regla de ancho de banda de Carson o simplemente regla de Carson [7, 8].

Una señal de FM se muestra en la Figura\(\PageIndex{5}\). En particular, la Figura\(\PageIndex{5}\) (a) muestra la función FM. El nivel (típicamente voltaje) de la señal de banda base determina la desviación de frecuencia de la portadora de su valor no modulado. El desplazamiento de frecuencia cuando la señal moduladora es un valor de CC\(x_{m}\) en su amplitud máxima se denomina desviación de frecuencia pico,\(\Delta f\). Entonces, si la señal moduladora cambia muy lentamente, el ancho de banda de la señal modulada es\(2\Delta f\).

Una señal moduladora sinusoidal que varía rápidamente produce una señal modulada con muchas bandas laterales discretas como se ve en la Figura\(\PageIndex{5}\) (b). Si la señal de banda base moduladora es de banda ancha, entonces las bandas laterales tienen un ancho de banda finito como se ve en la Figura\(\PageIndex{5}\) (c) y se requieren muchas para recuperar la señal de banda base original. Estas bandas laterales continúan indefinidamente en frecuencia pero reducen rápidamente su potencia alejándose de la frecuencia de la portadora no modulada. La regla de Carson proporciona una estimación del ancho\(98\%\) de banda que contiene la energía. Si la frecuencia máxima de la señal moduladora es\(f_{m}\), y el valor máximo de la forma de onda moduladora es\(x_{m}\) (lo que produciría una desviación de frecuencia de\(\Delta f\) si es CC), entonces la regla de Carson es que

\[\label{eq:8}\text{bandwidth required }=2\times (f_{m}+\Delta f) \]

FM de banda estrecha y banda ancha

El tipo más común de señal FM, como se usa en la radio de difusión FM, se llama FM de banda ancha, ya que la desviación de frecuencia máxima es mucho mayor que la frecuencia más alta de la señal moduladora o de banda base, es decir,\(\Delta f ≫ f_{m}\). En FM de banda estrecha,\(\Delta f\) está cerca de\(f_{m}\). La FM de banda estrecha utiliza menos ancho de banda pero requiere una técnica de demodulación más sofisticada.

Ejemplo\(\PageIndex{1}\): PAPR and PMEPR of FM Signals

Considera señales de FM cercanas en frecuencia pero cuyos espectros no se superponen.

1. ¿Qué son PAPR y PMEPR de una sola señal FM?
2. Qué son PAPR y PMEPR de una señal compuesta por dos señales FM de banda estrecha no correlacionadas, cada una de las cuales tiene un ancho de banda fraccional pequeño y que tiene la misma potencia promedio.

Solución

1. Una señal FM tiene una envolvente constante al igual que una sola sinusoide, y así\(\text{PAPR} = 1.414 = 3.01\text{ dB}\) y\(\text{PMEPR} = 1 = 0\text{ dB}\).
2. Dado que la modulación es relativamente lenta, cada una de las señales de FM se verá como señales de un solo tono y la señal combinada se verá como una señal de dos tonos. Sin embargo esto no es suficiente para resolver el problema. Se requiere un experimento de pensamiento para determinar la pseudo-portadora más grande cuando se combinan las señales de FM. Si la amplitud de cada tono es\(X\), entonces la amplitud cuando las formas de onda de la señal de FM se alinean es\(2X\). (Esto es lo mismo que el pico de una señal de dos tonos pero llegó de manera diferente). Entonces
   \[P_{\text{avg}}=\text{sum of the powers of each FM signal }=2k\frac{1}{2}X^{2}\nonumber \]
   donde\(k\) está una constante de proporcionalidad. Para PAPR,
   \[\label{eq:9}P_{P}=k(2X)^{2}\quad\text{and}\quad\text{PMEPR}=\frac{P_{P}}{P_{\text{avg}}}=\frac{k(2X)^{2}}{2k\frac{1}{2}X^{2}}=4=6.0\text{ dB} \]
   para PMEPR\(P_{\text{PEP}}=\text{ power of the pseudo-carrier }=k\frac{1}{2}(2X)^{2}\)
   y
   \[\label{eq:10}\text{PMEPR}=\frac{P_{P}''}{P_{\text{avg}}}=\frac{k\frac{1}{2}(2X)^{2}}{2k\frac{1}{2}X^{2}}=2=3.0\text{ dB} \]

2.4.4 Resumen de modulación analógica

La modulación analógica se utilizó en las primeras radios y en las radios celulares 1G. La transmisión de radio mediante modulación analógica, es decir, radio analógica, casi ha cesado ya que no utiliza el espectro de manera eficiente. La modulación digital junto con la corrección de errores, puede empacar mucha más información en un ancho de banda limitado. Una comparación final de las técnicas de modulación analógica se da en la Figura 2.5.1 enfatizando el PMEPR de AM y FM. El PMEPR de PM es el mismo que para FM.

Un acontecimiento particular en el desarrollo de la radio es ilustrativo de la relación entre la tecnología y los intereses empresariales. La modulación de frecuencia fue inventada por Edwin H. Armstrong y patentada en 1933 [9, 10]. FM es prácticamente libre de estática y claramente superior a la radio AM. Sin embargo, no se adoptó de inmediato en gran parte porque la radio AM se estableció en la década de 1930, y la adopción de FM habría resultado en el desguace de una gran infraestructura instalada (vista como una catástrofe comercial) y así la introducción de FM se retrasó décadas. ¡La mejor tecnología no siempre gana de inmediato! Los intereses comerciales y la gran inversión en una tecnología alternativa tienen mucho que ver con el éxito de una tecnología [11].

Con FM y PM hay dos conjuntos de bandas laterales con un conjunto por encima de la frecuencia portadora y el otro establecido a continuación. El operador en sí es de bajo nivel pero no está completamente suprimido. Ahora la modulación SSB se refiere a producir solo uno de los conjuntos de banda lateral. Hay tal cosa como SSB FM con solo unas pocas bandas laterales debajo (o por encima) del portador pero es más como una combinación de FM y AM [12], y nunca se desplegó.