2.8: Interferencia y Distorsión

La demodulación de una señal recibida equivale a reconstruir el diagrama de constelación original de la señal de modulación. Los errores son causados por interferencia, ruido y distorsión. Comúnmente, los tres efectos se agrupan y se llaman interferencia y se tratan como si tuvieran aleatoriedad gaussiana similar al ruido. Idealmente no hay interferencia para que un receptor detecte correctamente el símbolo correcto tras la demodulación. La interferencia resultará en quizás una elección incorrecta del símbolo y, por lo tanto, un error. Los errores se pueden reducir aumentando el nivel de señal en el transmisor, aumentando así la relación señal/interferencia. Esto viene con un precio ya que aumentar el nivel de señal resulta en mayores niveles de interferencia para otras radios. La solución a la que se llegó es asegurar que si hay un error, entonces el símbolo detectado incorrectamente no esté a más de un símbolo del símbolo real. Esto significa que hay como máximo un bit de error mientras que un símbolo puede transportar múltiples bits de información. La codificación de corrección de errores se puede usar entonces para eliminar errores.

Nota

Emile Baudot utilizó 'códigos grises en telegrafía en 1878 [15]. El nombre deriva de Frank Gray quien los utilizó en un esquema de codificación de modulación por código de pulso [16].

En QAM, los símbolos se asignan a puntos de constelación usando un código Gray en el que los símbolos vecinos más cercanos cambian solo en un bit [17], por ejemplo, ver Figura 2.8.18 (c). Por lo tanto, solo hay un bit de entre muchos que estará en error si hay ruido e interferencia. Si el error es mayor, entonces se usa un orden inferior de modulación de modo que si se detecta incorrectamente un símbolo, entonces el símbolo incorrecto está a lo sumo a un símbolo del símbolo transmitido real.

2.11.1 Interfaz cocanal

La señal mínima detectable en los sistemas inalámbricos convencionales está determinada por la relación señal/interferencia (SIR) en la entrada a un receptor, donde la interferencia se refiere al ruido así como a la interferencia de otras radios. En los sistemas inalámbricos celulares la interferencia dominante es de otras radios y se denomina interferencia cocanal. El grado en que se puede controlar la interferencia cocanal tiene un gran efecto en la capacidad del sistema. El control de la interferencia cocanal se logra en gran medida controlando los niveles de potencia

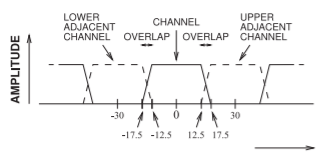
Figura\(\PageIndex{1}\): Canales adyacentes que muestran solapamiento en los sistemas celulares AMPS y DAMPS.

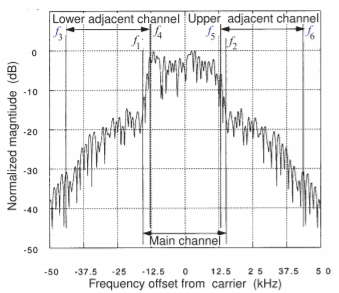
Figura\(\PageIndex{2}\): Espectro que define límites de integración de canal adyacente y canal principal mediante un esquema de modulación\(π/4\) -DQPSK.

en la estación base y en las unidades móviles.

2.11.2 Interfaz de canal adyacente

La interferencia de canal adyacente resulta de varios factores. Dado que el filtrado no es ideal, existe una superposición inherente de canales vecinos (Figura\(\PageIndex{1}\)). Por esta razón, los canales adyacentes se asignan a diferentes celdas. El comportamiento no lineal de los transmisores también contribuye a la interferencia de canales adyacentes. Por lo tanto, la caracterización de fenómenos no lineales es importante en el diseño de RF. El espectro de una señal modulada usando un esquema QPSK se muestra en la Figura\(\PageIndex{2}\). La señal entre frecuencias\(f_{1}\) y\(f_{2}\) se debe al propio esquema de modulación digital. La mayor parte de la señal fuera de esta región se debe a efectos no lineales y se denomina rebrote espectral, un proceso similar a la distorsión de una señal de dos tonos. Usando los límites de frecuencia definidos en la Figura\(\PageIndex{2}\), el ACPR de canal inferior se define como

\[\label{eq:1}\text{ACPR}_{\text{ADJ, LOWER}}=\frac{\text{Power in lower adjacent channel}}{\text{Power in main channel}}=\frac{\int_{f_{3}}^{f_{4}}X(f)df}{\int_{f_{1}}^{f_{2}}X(f)df} \]

donde\(X(f)\) es la densidad de potencia espectral de la señal de RF. El canal superior ACPR,\(\text{ACPR}_{\text{ADJ, UPPER}}\), se define de manera similar. Cuando se hace referencia a ACPR sin indicar si es ACPR superior o inferior, se usa el mayor (es decir, el peor) de\(\text{ACPR}_{\text{ADJ, LOWER}}\) y\(\text{ACPR}_{\text{ADJ, UPPER}}\). La ACPR generalmente se expresa en decibelios, y si bien la definición es tal que ACPR será menor que uno, cuando se expresa en decibelios, a menudo se usa un número positivo (por ejemplo,\(20\text{ dB}\) para un ACPR de\(0.01\) más que el correcto\(−20\text{ dB}\), así que tenga cuidado).

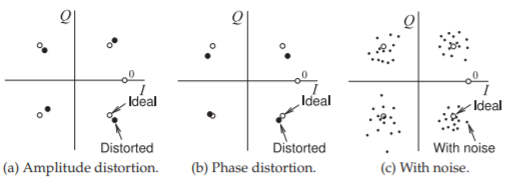
Figura\(\PageIndex{3}\): Impacto de los deterioros de señal en el diagrama de constelaciones de QPSK.

2.11.3 Diagramas de ruido, distorsión y constelación

El ruido y la distorsión no lineal afectan la capacidad de demodular correctamente las señales y determinar los símbolos transmitidos. Estos efectos de distorsión pueden describirse por su efecto sobre el diagrama de constelación recibido, ver Figura\(\PageIndex{3}\), que muestra el estado del sistema en el instante de muestreo determinado por la portadora recuperada.

La Figura\(\PageIndex{3}\) (a) muestra el efecto de los errores de distorsión de amplitud sobre la señal demodulada. El muestreo de la señal recibida será un punto de constelación distorsionado que no corresponde al punto de constelación ideal. La unidad DSP debe tomar una decisión sobre qué punto de constelación ideal corresponde al punto de constelación distorsionado. El efecto de la distorsión de fase se muestra en la Figura\(\PageIndex{3}\) (b). Tanto la distorsión de amplitud como de fase podrían ocurrir en el transmisor o receptor, o ser el resultado de efectos en la trayectoria de la señal. La Figura\(\PageIndex{3}\) (c) muestra el efecto del ruido sobre el deterioro de la señal. Nuevamente el punto de constelación extraído de la señal RF se ve afectado por el ruido y los puntos de constelación muestreados e ideales no coinciden. Asociar el punto de constelación extraído del muestreo de la forma de onda RF recibida con el punto de constelación incorrecto crea un error de símbolo y por lo tanto un error de bit. Los errores en la recuperación del portador distorsionan aún más el diagrama de constelación. Todos los sistemas de radio digital móvil ajustan el nivel de la señal RF transmitida, y adicionalmente en la radio celular 4G y 5G cambian el orden de modulación, por lo que se obtiene una BER aceptable. Usar más energía de la necesaria reduce la duración de la batería y causa interferencias adicionales en otras radios.

2.11.4 Comparación de la modulación GMSK y\(\pi /4\) DQPSK

En esta sección se presentan los resultados del tipo de análisis que se realiza para caracterizar los métodos de modulación. Existe una gran cantidad de literatura que documenta el desempeño de esquemas de modulación y suele ser el resultado de un modelo de error supuesto, es decir, el tipo de interferencia y la descripción estadística de esa interferencia, y luego simulaciones numéricas. Esta sección compara los métodos de modulación\(π/4\) GMSK y DQPSK, los primeros métodos de modulación digital celular ampliamente utilizados.

Las constelaciones de GMSK de 4 estados, ver Figura 2.6.2 (b), y\(π/4\) DQPSK, ver Figura 2.8.8 son las mismas excepto que con\(π/4\) DQPSK la constelación gira cada tick de closk. En GMSK la amplitud de la portadora modulada permanece casi constante y la frecuencia de la portadora varía lentamente. Con GMSK los símbolos corresponden a diferentes frecuencias de RF por lo que no es posible que los símbolos con frecuencias en extremos opuestos del rango de frecuencias hagan una transición directa sin atravesar los otros puntos del símbolo. Esta larga transición resulta en la reducción de la eficiencia de modulación de GMSK. Con

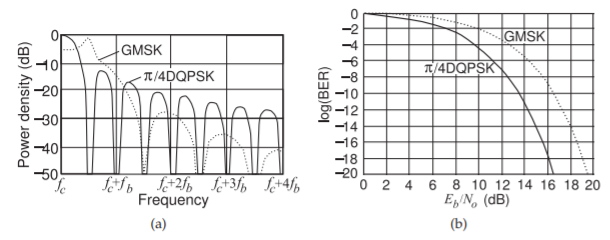
Figura\(\PageIndex{4}\): Comparación de GMSK y\(π/4\) DQPSK: (a) densidad espectral de potencia en función de la desviación de frecuencia de la portadora; y (b) BER versus relación señal/ruido (SNR) como\(E_{b}/N_{o}\) (o energía por bit dividida por ruido por bit).

\(π/4\)DQPSK hay transiciones directas y la magnitud del fasor RF no permanece constante. Entonces, si bien se obtiene una mayor eficiencia de modulación en comparación con GMSK,\(π/4\) -DQPSK tiene una envolvente significativamente variable en el tiempo.

El formato de modulación utilizado afecta la elección de los circuitos, la duración de la batería y la tolerancia del sistema al ruido. La figura\(\PageIndex{4}\) contrasta la densidad de potencia frente a la frecuencia y tasa de error de bits (BER) de la modulación GMSK y QPSK de cuatro estados. En la Figura\(\PageIndex{4}\) (a),\(f_{c}\) se encuentra la frecuencia portadora y\(f_{b}\) es la frecuencia de bits, y se ve que GMSK y QPSK tienen diferentes formas espectrales. La mayor parte de la energía está contenida dentro del ancho de banda definido por la mitad de la frecuencia de bits (esta es la frecuencia del símbolo ya que hay dos bits por símbolo). En múltiplos de la frecuencia de bits, la densidad de potencia con GMSK es mucho menor que con QPSK, lo que resulta en menos interferencia (interferencia de canal adyacente [ACI]) con radios en canales adyacentes. Esta es una métrica importante con radios que es capturada por la relación de potencia del canal adyacente (ACPR), la relación de la potencia en el canal adyacente a la potencia en el canal principal. Otra métrica importante es la BER que se incrementa por el ruido en el canal principal con diferentes formatos de modulación que difieren en su susceptibilidad a la interferencia. El nivel de ruido es capturado por la relación de la potencia en un bit,\(E_{b}\), a la potencia de ruido,\(N_{o}\), en el intervalo de tiempo de un bit. Esta relación,\(E_{b}/N_{o}\) (leída como E B N O), está directamente relacionada con la relación señal/ruido (SNR). En particular, considere la gráfica de la BER frente a la\(E_{b}/N_{o}\) mostrada en la Figura\(\PageIndex{4}\) (b), donde se puede observar que\(π/4\) DQPSK es menos susceptible al ruido que GMSK.

2.11.5 Magnitud del vector de error

La métrica de magnitud vectorial de error (EVM) caracteriza la precisión de la forma de onda en las instancias de muestreo y por lo tanto está directamente relacionada con la BER en radio digital. EVM captura el efecto combinado de las no linealidades del amplificador, los desequilibrios de amplitud\(I\) y fase de caminos separados y de\(Q\) señal, ondulación de amplitud en banda (por ejemplo, debido a filtros), ruido, mezcla no ideal, recuperación de portadora no ideal e inexactitudes DAC.

El EVM es una medida de la salida de un fasor muestreado del ideal

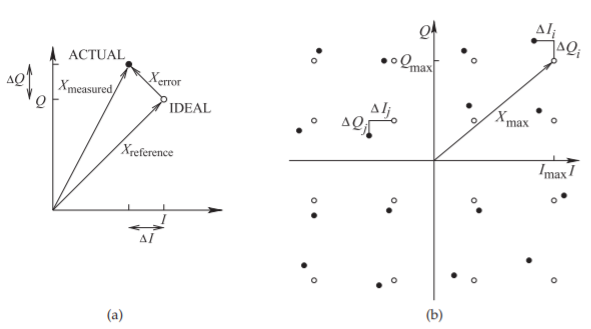
Figura\(\PageIndex{5}\): Diagrama de constelación parcial que muestra las cantidades utilizadas en el cálculo de EVM: (a) definición de señales de error y de referencia; y (b) cantidades de error utilizadas cuando los puntos de constelación tienen diferentes potencias.

fasor localizado en el punto de la constelación (ver Figura\(\PageIndex{5}\) (a)). Introduciendo un vector de error\(X_{\text{error}}\), y un vector de referencia\(X_{\text{reference}}\),, que apunta al punto de constelación ideal, el EVM se define como la relación de la magnitud del vector de error con respecto al vector de referencia de manera que

\[\label{eq:2}\text{EVM}=\frac{|X_{\text{error}}|}{|X_{\text{reference}}|} \]

Expresar el error y la referencia en términos de las facultades\(P_{\text{error}}\) y\(P_{\text{reference}}\), respectivamente, permite que la EVM se exprese como

\[\label{eq:3}\text{EVM}=\sqrt{\frac{P_{\text{error}}}{P_{\text{reference}}}} \]

en decibelios,

\[\label{eq:4}\text{EVM}_{\text{dB}}=10\log\frac{P_{\text{error}}}{P_{\text{reference}}}=20\log\frac{|X_{\text{error}}|}{|X_{\text{reference}}|} \]

o como porcentaje,

\[\label{eq:5}\text{EVM}(\%)=\frac{X_{\text{error}}}{X_{\text{reference}}}\cdot 100\% \]

Si el formato de modulación da como resultado puntos de constelación que tienen diferentes potencias (por ejemplo, con 16-QAM), el punto de constelación con la potencia más alta se usa como referencia y se promedia el error en cada punto de constelación. Con referencia a la Figura\(\PageIndex{5}\), y con puntos de\(N\) constelación,

\[\label{eq:6}\text{EVM}=\sqrt{\frac{\frac{1}{N}\sum_{i=1}^{N}(\Delta I_{i}^{2}+\Delta Q_{i}^{2})}{X_{\text{max}}^{2}}} \]

donde\(|X_{\text{max}}|\) es la magnitud del vector de referencia al punto de constelación más distante y\(\Delta I_{i}\) y\(\Delta Q_{i}\) son los\(Q\) desplazamientos\(I\) y del punto de constelación real y el punto de constelación ideal. Tenga en cuenta que para QAM el diagrama de constelación corresponde a un diagrama de fasores que se está normalizando continuamente al nivel promedio de la señal de RF recibida. En el diagrama de constelación las\(Q\) coordenadas\(I\) y corresponden a cantidades RMS. Así\(|X_{\text{max}}|\) es una cantidad RMS. La EVM se expresa tradicionalmente como un porcentaje.

Una medida similar de la calidad de la señal es la relación de error de modulación (MER), una medida de la potencia de señal promedio a la potencia de error promedio. En decibelios se define como

\[\label{eq:7}\text{MER}|_{\text{dB}}=10\log\frac{\frac{1}{N}\sum_{i=1}^{N}(I_{i}^{2}+Q_{i}^{2})}{\frac{1}{N}\sum_{i=1}^{N}(\Delta I_{i}^{2}+\Delta Q_{i}^{2})}=10\log\frac{\sum_{i=1}^{N}(I_{i}^{2}+Q_{i}^{2})}{\sum_{i=1}^{N}(\Delta I_{i}^{2}+\Delta Q_{i}^{2})} \]

La ventaja del MER es que se relaciona directamente con el SNR.

Otra cantidad relacionada tanto con los conceptos EVM como MER es el margen de implementación,\(k\). El margen de implementación es una medida del desempeño de hardware particular y es desarrollado por grupos de diseño basados en la experiencia con diseños similares. El EVM requerido se puede estimar a partir del margen de implementación de hardware:

\[\label{eq:8}\text{EVM}_{\text{required}}=\sqrt{\frac{k}{\text{SNR}\cdot\text{PMEPR}}} \]

En decibelios,

\[\label{eq:9}\text{EVM}_{\text{dB, required}}=k_{\text{dB}}-\text{SNR}_{\text{dB}}-\text{PMEPR}_{\text{dB}} \]

Ejemplo\(\PageIndex{1}\): Modulation Error Ratio

Una señal modulada 16-QAM tiene un valor máximo de rf fasor rms de\(4\text{ V}\). Si el ruido en la señal tiene un valor rms de\(0.1\text{ V}\), ¿cuál es la relación de error de modulación de la señal modulada?

Solución

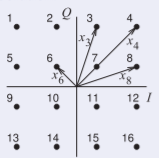
Figura\(\PageIndex{6}\)

Se debe determinar la distancia desde el origen hasta cada uno de los puntos de constelación, pero debido a la simetría solo se\(x_{8}\) deben calcular las distancias\(x_{3},\: x_{4},\: x_{7}(= x_{6})\) y. La amplitud máxima del fasor RF es\(4\text{ V}\), por lo tanto, la longitud\(x_{4} = 4\), con componentes

\[\begin{aligned}I_{4}&=Q_{4}=\sqrt{x_{4}^{2}/2}=2.828 \\ I_{6}&=\left(-\frac{1}{3}\right)\cdot I_{4}=-0.943 =-Q_{6},\text{ so }x_{6}=1.333 \\ I_{3}&=0.943;\: Q_{3}=2.828,\text{ so }x_{3}=2.981=x_{8}\end{aligned}\nonumber \]

y

\[\text{MER}=\frac{\sum_{i=1}^{16}(x_{i}^{2})}{\sum_{i=1}^{16}(x_{\text{noise}}^{2})}\nonumber \]

El cálculo se simplifica considerando solo un cuadrante y el ruido,\(x_{\text{noise}} = 0.1\), es el mismo para cada punto de constelación.

\[\begin{aligned}\text{MER}&=\frac{4(x_{3}^{2}+x_{4}^{2}+x_{6}^{2}+x_{8}^{2})}{16\cdot x_{\text{noise}}^{2}}\\ &=\frac{4(2.981^{2}+4^{2}+1.333^{2}+2.981^{2})}{16\cdot 0.1^{2}}=\frac{142.2}{0.16}=888.8 \\ \text{MER}|_{\text{dB}}&=10\log (888.8)=25.9\text{ dB}\end{aligned}\nonumber \]

Compare esto con la SNR calculada en los puntos individuales de la constelación:

\[\begin{aligned}\text{Point }3,\text{ SNR }&=x_{3}^{2}/0.1^{2}=888.6=29.5\text{ dB} \\ \text{Point }4,\text{ SNR }&=x_{4}^{2}/0.1^{2}=1600=32.0\text{ dB} \\ \text{Point }7,\text{ SNR }&=x_{7}^{2}/0.1^{2}=177.7=22.5\text{ dB}\end{aligned}\nonumber \]