3.14: Arquitecturas Modernas

Esta sección analiza las arquitecturas de transmisor y receptor en las generaciones anteriores a la radio definida por software (como se usa en 4G y 5G). Se trata de arquitecturas que podrían implementarse en hardware analógico.

3.7.1 Arquitecturas de receptor

Es más difícil lograr un alto rendimiento para un receptor que para un transmisor.

o un transmisor. Los receptores de comunicación suelen utilizar la mezcla de la señal de RF con una señal fija llamada LO para producir una réplica de frecuencia más baja de la señal de RF modulada. Algunas arquitecturas de receptor utilizan una etapa de mezcla, mientras que otras usan dos etapas. En los sistemas celulares, el receptor debe ser lo suficientemente sensible como para detectar señales de\(100\text{ fW}\) o menos.

Algunas de las arquitecturas utilizadas en los receptores modernos se muestran en la Figura\(\PageIndex{2}\). La figura\(\PageIndex{2}\) (a) es la arquitectura superheterodina en casi la misma forma que se ha utilizado desde hace un siglo. Las características clave de esta arquitectura son que hay dos etapas de mezcla, y el filtrado es necesario para suprimir los productos de mezcla espurios. Cada etapa de mezcla tiene su propio VCO. El receptor reduce progresivamente la frecuencia de la señal portadora de información. El mezclador de rechazo de imagen en el cuadro discontinuo logra el rechazo de la frecuencia de imagen para producir un IF (o frecuencia de banda base) que puede ser muestreado directamente. Sin embargo, es difícil lograr el equilibrio de amplitud y fase requerido. En cambio, a veces se utiliza la arquitectura que se muestra en la Figura\(\PageIndex{2}\) (b). El filtro entre los dos mezcladores puede ser bastante grande. Por ejemplo, si el

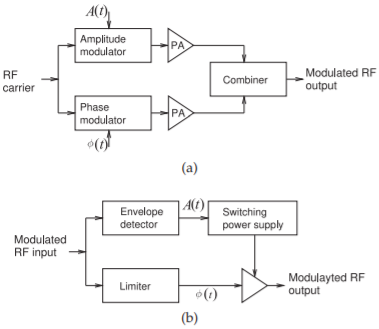
Figura\(\PageIndex{1}\): Arquitecturas de moduladores polares: (a) componentes de amplitud y fasemodulación amplificados por separado y combinados; y (b) la amplitud utilizada para modular una fuente de alimentación que impulsa un amplificador de saturación con entrada modulada en fase.

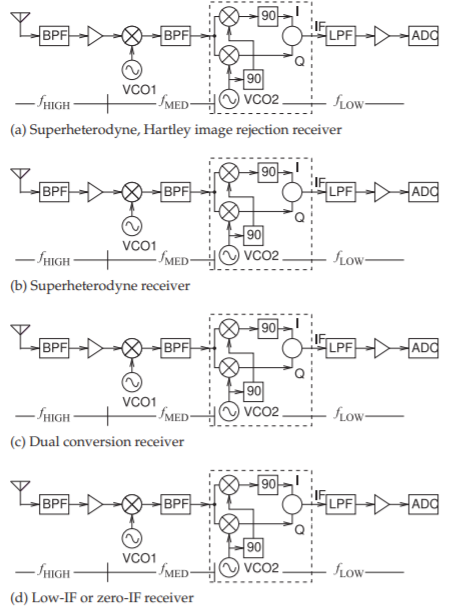
Figura\(\PageIndex{2}\): Arquitecturas de receptores modernos: (a) receptor superheterodino que utiliza la arquitectura Hartley para rechazo de imagen; (b) receptor superheterodino; (c) receptor de doble conversión; y (d) receptor de baja IF o Cero-IF. BPF, filtro paso banda; LPF, filtro paso bajo; ADC, convertidor analógico-digital; VCO, oscilador controlado por voltaje;\(90,\: 90^{\circ}\) desfasador;\(f_{\text{HIGH}},\: f_{\text{MED}},\) e\(f_{\text{LOW}}\) indican secciones de frecuencia relativamente alta, media y baja.

señal entrante es\(1\text{ GHz}\), la frecuencia de la señal después del primer mezclador podría ser\(100\text{ MHz}\).

Los filtros son más pequeños y tienen un mayor rendimiento a frecuencias más altas. Esto se explota en el receptor de doble conversión mostrado en la Figura\(\PageIndex{2}\) (c). Esto es similar a la arquitectura superheterodina tradicional excepto que el IF entre los dos mezcladores es alto. Por ejemplo, si la señal entrante es\(1\text{ GHz}\), la salida del primer mezclador podría ser\(3\text{ GHz}\). Esta arquitectura también permite un amplio funcionamiento de radio con la banda seleccionada al elegir las frecuencias de los dos osciladores locales.

El receptor de IF bajo o de IF cero que se muestra en la Figura\(\PageIndex{2}\) (d) usa menos hardware y es común en aplicaciones de comunicación menos exigentes. En sistemas de alto rendimiento, como el sistema de telefonía celular, esta arquitectura requiere más tiempo de diseño así como circuitos de calibración para recortar las rutas I y Q para que coincidan estrechamente.

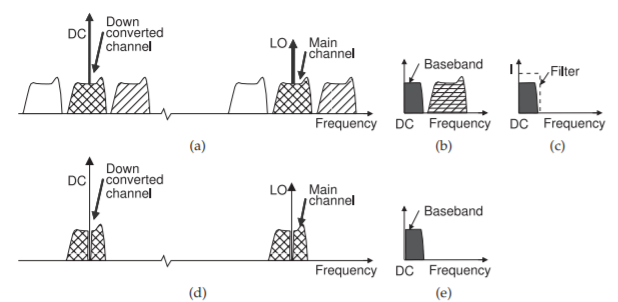
Figura\(\PageIndex{3}\): Conversión de frecuencia usando mezcla homodina: (a) el espectro con un LO grande y los productos de baja frecuencia después de la conversión descendente; (b) el espectro de banda base que muestra solo frecuencias positivas; (c) el espectro de banda base después de la mezcla; (d) espectros de conversión descendente cuando la señal de radio no tiene contenido espectral a la frecuencia portadora; y (e) la señal convertida descendentemente filtrada de paso bajo en (d).

3.7.2 Conversión de frecuencia homodina

La mezcla y detección homodina es una de las primeras tecnologías de receptor inalámbrico y se utiliza en la radio AM. En la mezcla homodina, la portadora de una señal modulada se regenera y sincroniza en fase con la frecuencia portadora entrante. La mezcla de la portadora con la señal de RF da como resultado una señal IF centrada alrededor de la frecuencia cero.

Los espectros de señal en la mezcla homodina se muestran en la Figura\(\PageIndex{3}\). En la Figura\(\PageIndex{3}\) (a), las señales de RF se muestran en el lado derecho y las señales de banda base se muestran en el lado izquierdo. Es habitual mostrar frecuencias tanto positivas como negativas en las frecuencias más bajas para que el proceso de conversión sea más fácil de ilustrar. Por supuesto, las frecuencias negativas no existen. La característica de la mezcla homodina es que el LO corresponde al portador y está en medio del canal de RF deseado. Los componentes de la señal de RF se mezclan con el LO, y parece que todo el espectro de RF se desplaza hacia abajo alrededor de CC. Por supuesto, el espectro de banda base real solo se define para frecuencias positivas, por lo que las señales de banda base de frecuencia negativa y las señales de banda base de frecuencia positiva se combinan para producir el espectro de banda base detectado que se muestra en la Figura\(\PageIndex{3}\) (b). Con otros esquemas de modulación, esta posible pérdida de información se evita usando la demodulación en cuadratura. Una señal modulada en amplitud tiene bandas laterales de modulación idénticas, por lo que el colapso de las frecuencias positivas y lo que se muestra como negativas en la banda base no da como resultado ninguna pérdida de información. Luego se usa un simple circuito de detección de amplitud, como un rectificador, y la señal rectificada se pasó (típicamente) directamente a un altavoz.

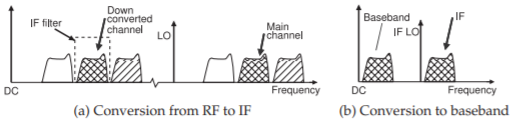
Figura\(\PageIndex{4}\): Conversión de frecuencia mediante mezcla superheterodina.

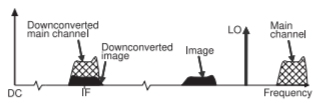
Figura\(\PageIndex{5}\): Conversión de frecuencia usando mezcla heterodina que muestra el efecto de distorsión de la imagen con la imagen convertida hacia abajo superponiendo el canal principal convertido a la baja.

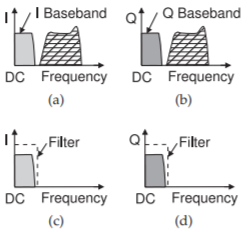
Figura\(\PageIndex{6}\): Conversión de frecuencia usando mezcla en cuadratura de conversión directa: (a) el espectro de banda base en la salida I del receptor; (b) el espectro de banda base en la salida Q del receptor; y (c y d) el espectro de los canales I y Q siguientes.

3.7.3 Conversión de frecuencia heterodina

En la mezcla heterodina, el LO generado localmente y el canal principal de RF están separados en frecuencia, como se muestra en la Figura\(\PageIndex{4}\) (a). En esta figura las señales de RF (mostradas como tres canales discretos en el lado derecho del espectro) se mezclan con el LO para producir señales a una frecuencia más baja. Esta frecuencia más baja no suele ser la frecuencia de banda base final, y así se llama la frecuencia intermedia (IF). El IF del canal principal está en la frecuencia de diferencia de la señal RF y el LO. Hay varios refinamientos importantes en esto. El primero de ellos se refiere a limitar el número de señales que pueden mezclarse con el LO. Esto se hace usando un filtro de preselección de RF. Para ver las dificultades introducidas por el canal de imagen, considere la conversión de frecuencia a una frecuencia intermedia descrita en la Figura\(\PageIndex{5}\). El filtrado reduce el nivel del canal de imagen como se muestra en la Figura\(\PageIndex{5}\) (a). Obsérvese que el canal principal y su imagen son equidistantes de la LO, ver Figura\(\PageIndex{5}\). Ambos se convierten a la misma frecuencia IF. En el peor de los casos, la imagen IF podría ser mayor que la del canal deseado.

3.7.4 Receptor de conversión directa

Los receptores de conversión directa de IF cero son similares a los receptores homodínos en cuadratura en que el LO se coloca cerca del centro del canal de RF La característica importante de los receptores de conversión directa es que solo hay un nivel de mezcla. El proceso de conversión se describe en la Figura\(\PageIndex{6}\). Una ventaja particular de la conversión directa es que se eliminan los filtros IF relativamente grandes. Se implementan invariablemente como cuadratura

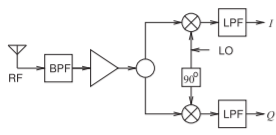
Figura\(\PageIndex{7}\): Desmodulador en cuadratura de conversión directa.

demoduladores, ver Figura\(\PageIndex{7}\). utilizado en teléfonos celulares ya que utiliza poca energía de CC, y por lo tanto extiende la duración de la batería, y es compatible con CI monolíticos. La conversión directa es ahora el método preferido de conversión descendente.

La principal no idealidad de este diseño es el desplazamiento de CC en el espectro de conversión descendente. La compensación de CC resulta principalmente de la auto-mezcla, o rectificación, de la LO. Este desplazamiento de CC puede ser mucho mayor que la señal convertida descendentemente. Una forma de hacer frente al desplazamiento de CC es filtrar paso alto la señal convertida de manera descendente, pero el filtrado paso alto requiere un componente pasivo grande (por ejemplo, un condensador en serie), al menos para evitar los problemas de rango dinámico de los filtros activos. El filtrado de paso alto de la señal convertida hacia abajo necesariamente arroja información en el espectro de la señal, y solo es satisfactorio hacer esto si hay muy poca información alrededor de DC para empezar.

El principal esfuerzo de diseño con convertidores de IF cero es superar el problema de desplazamiento de CC y, en menor medida, hacer frente a la fluctuación del LO. Sin embargo existe un esquema utilizado en 4G y 5G que supera estas limitaciones. Esto se discutirá en los capítulos siguientes.

3.7.5 Receptor de IF bajo

En un receptor de baja IF, la mezcla heterodina de una sola etapa se utiliza para convertir la portadora de RF modulada a una frecuencia justo por encima de CC, tal vez unos pocos cientos de kilohercios o unos pocos megahercios, dependiendo del ancho de banda del canal de RF. Al hacer esto, se evita el problema de desplazamiento de CC de un receptor de conversión directa. Este desplazamiento de frecuencia puede ser de solo unos cientos de hercios para ser efectivo. La conversión de IF baja es ahora el método preferido de conversión descendente en teléfonos celulares, ya que requiere muy poco uso de masa, no requiere filtros IF grandes y es compatible con CI monolíticos. A veces, la conversión bajo-IF se conoce como conversión descendente directa, pero hay una diferencia sutil.

3.7.6 Conversión de submuestreo analógico a digital

Los receptores de submuestreo superan el problema de desplazamiento de CC típico de otros receptores de conversión directa. La idea es muestrear la señal de RF modulada en un subarmónico de la portadora de la señal de RF a convertir. La frecuencia de muestreo debe ser al menos el doble del ancho de banda de la señal de banda base y el ancho de banda en modo pista debe ser mayor que la frecuencia portadora. Así, la apertura de muestreo es el parámetro crítico y debe ser varias veces menor que el periodo del portador. Afortunadamente los tiempos de apertura de los circuitos de seguimiento CMOS son adecuados. Es fundamental que se utilice un filtro de preselección de RF para eliminar los interferentes no deseados y el ruido fuera de la banda de comunicación. El aliasing de señales fuera del ancho de banda de Nyquist sobre la señal de banda base es una consecuencia del submuestreo. Las señales de canal adyacentes se convierten sin aliasing, pero éstas quedarán fuera del ancho de banda del

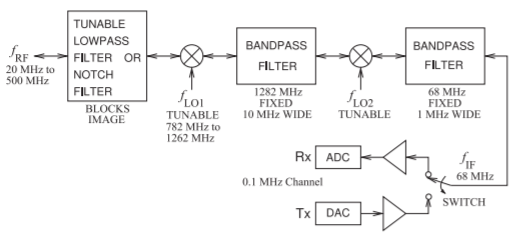
Figura\(\PageIndex{8}\): Transceptor bilateral de doble conversión para operación de banda ancha de una radio militar o de emergencia.

señal de banda base. El ruido de parpadeo en el reloj de muestreo se multiplica por la relación de submuestreo y aparece como ruido adicional en la banda base. Esta fue en un momento una opción muy atractiva pero ha sido superada por el receptor Low-IF.

3.7.7 Primera conversión IF a BaseBind

En una arquitectura de conversión superheterodina hay dos etapas heterodinas, con el IF de la primera etapa en sistemas modernos en el rango de\(20\) a\(200\text{ MHz}\). La asignación de frecuencias se conoce como planificación de frecuencias, y esta es tratada como propietaria por los principales proveedores de radio. Esta IF se convierte entonces en una IF mucho más baja, típicamente alrededor\(100\text{ kHz}\) de unos pocos megahercios por encima de la frecuencia central de la señal de banda base. Esta frecuencia generalmente se llama banda base, pero estrictamente no se debe a que la señal aún esté desplazada en frecuencia de CC. Algunas arquitecturas de conversión directa dejan la primera etapa de mezcla heterodina en su lugar y utilizan la conversión directa de la primera IF a banda base (banda base verdadera, alrededor de CC).

3.7.8 Receptor Bilateral de Doble Conversión

Los receptores considerados hasta ahora son adecuados para comunicaciones de banda estrecha típicas de radio móvil punto a punto y de consumo. Hay muchas situaciones en las que el alcance de las señales de RF recibidas o transmitidas cubre un ancho de banda muy amplio, como con radios de emergencia, televisión y comunicaciones militares. Típicamente, sin embargo, el ancho de banda instantáneo es pequeño. Si se utilizan arquitecturas front-end de RF de banda estrecha, se requeriría un banco de filtros conmutable y esto resultaría en una radio poco prácticamente grande. Una solución para cubrir anchos de banda RF muy amplios es la arquitectura del transceptor de doble conversión que se muestra en la Figura\(\PageIndex{8}\). Se muestra el plan de frecuencias de una radio típica usando\(0.1\text{ MHz}\) canales entre\(20\text{ MHz}\) y\(500\text{ MHz}\). La característica clave de esta radio es que se utilizan mezcladores bidireccionales. Siguiendo la cadena de RF de izquierda a derecha, la RF se mezcla primero en frecuencia, se filtra en paso de banda usando un filtro de alta\(Q\) distribución y luego se convierte a una frecuencia más baja que puede ser muestreada directamente por un ADC. Un filtro pasivo de rendimiento mucho mayor (y por lo tanto bidireccional) se puede realizar a frecuencias de gigahercios que a unas pocas decenas de megahercios. Al transmitir, la función es similar, con los mezcladores y LO reutilizados. Como receptor, el filtro de muesca o filtro de paso bajo se utiliza para bloquear la frecuencia de imagen del primer mezclador de manera que solo se presente el IF de banda lateral superior al primer filtro de paso de banda. El filtro paso bajo o muesca puede ser fijo, aunque, con el plano mostrado, debe haber al menos dos estados de los filtros. Al transmitir, los filtros paso bajo o notch evitan que la frecuencia de la imagen sea radiada.