5.6: Ganancia de procesamiento

En radio digital la señal demodulada es una señal binaria que incluye bits de información, bits de codificación, así como bits que están en error lo que contribuye a una tasa de error de bits en bruto (BER). En el receptor, la decodificación crea un flujo de bits más pequeño con solo los bits de información y que tiene una BER relativamente baja. Otra forma de ver lo que sucede es que la relación señal/interferencia (SIR) de la señal decodificada dividida por la SIR de la señal bruta representa una ganancia y esta ganancia se denomina ganancia de procesamiento. En la radio celular 2G esta ganancia de procesamiento también se llama ganancia de codificación. Con 3G se utilizan códigos de ensanchamiento además de los códigos de corrección de errores con ambos reduciendo la tasa de errores de bits pero ahora la ganancia de desensanchamiento se denomina ganancia de ensanchamiento y la ganancia de la codificación de corrección de errores se denomina ganancia de codificación. La ganancia de procesamiento es ahora el producto de la ganancia de propagación y la ganancia de codificación. Con 4G y 5G las funciones de los códigos de propagación y los códigos de corrección de errores se fusionan por lo que solo se usa el término ganancia de procesamiento.

5.6.1 Energía de un Bit

La ganancia de procesamiento (\(G_{P}\)) ocurre cuando se desmodula y recupera un flujo de bits de información y es la relación de la SIR de la señal procesada con respecto a la SIR de la señal no procesada, por lo que\(G_{P}\) captura la cantidad que aumenta la SIR. \(G_{P}\)es una medida de la inmunidad adicional al ruido obtenida

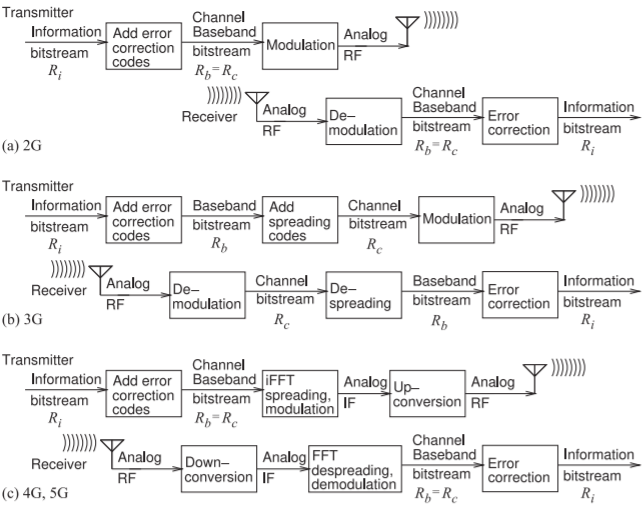
Figura\(\PageIndex{1}\): Flujo de información en radio celular digital con\(R_{i},\: R_{b},\) y\(R_{c}\) siendo la información, banda base y velocidades de bits de canal, respectivamente.

mediante decodificación y demodulación. Existen varias fórmulas para\(G_{P}\) depender de si la señal procesada es el flujo de bits de banda base con o sin codificación de corrección de errores, y si la señal no procesada es la señal de RF analógica, el flujo de bits de canal o el flujo de símbolo de canal (es decir, chip). El procesamiento de ganancia es un concepto esencial en la radio celular y realmente es lo que la hace funcionar. A continuación, se hará referencia a tres flujos de bits en el transmisor los cuales serán recuperados en el receptor. El primero es el flujo de bits de información con una tasa de bits\(R_{i}\) (en unidades de\(\text{bit/s}\)). Para esta corrección de errores se puede utilizar la codificación para producir un flujo de bits de banda base con tasa de bits de banda base\(R_{b} > R_{i}\). En algunas generaciones de radio, el flujo de bits de banda base se modula en una portadora y el flujo de bits de banda base es el mismo que el flujo de bits de canal. Los flujos de bits se muestran en la representación en la Figura\(\PageIndex{1}\) (a) del flujo de información en radio celular 2G.

En la radio celular 3G los códigos de difusión relativamente rápidos se fusionaron con el flujo de bits de banda base para producir un flujo de bits de canal mucho más rápido con tasa de\(R_{c} ≫ R_{b}\) bits La introducción de este tercer flujo de bits separado es la representación en la Figura\(\PageIndex{1}\) (b) del flujo de información en la radio celular 3G. El tercer flujo de bits es el flujo de bits de canal con tasa de bits\(R_{c}\) y este es el flujo de bits que se modula para producir una señal modulada con un diagrama de constelación donde representa cada símbolo\(b\text{ bits}\).

En 4G y 5G los códigos de corrección de errores de radio celular se fusionan con el flujo de bits de información para producir un flujo de bits de banda base y esto se propaga durante una primera etapa del proceso de modulación que produce una señal modulada de frecuencia intermedia analógica. Los detalles de este proceso se darán más adelante. No hay un código de ensanchamiento separado para que los flujos de bits de banda base y canal sean los mismos y\(R_{c} = R_{b}\).

La derivación de las ganancias de codificación, ensanchamiento y procesamiento se basa en la energía de un bit y la energía del ruido en el intervalo correspondiente a un bit. Se denota la energía de un bit en el\(x\) ésimo flujo de bits (\(x = i,\: b,\: c\)para información, banda base y canal respectivamente)\(E_{b, x}\) y se denota la energía del ruido correspondiente a la duración del bit\(N_{o, x}\). El equivalente digital de la SIR analógica es\(E_{b}/N_{o}\) (pronunciado E-B-N-O para EBNO) y la SIR efectiva del flujo de bits\(x\) th es

\[\label{eq:1}\text{SIR}_{\text{eff, }x}=\frac{E_{b, x}}{N_{o, x}} \]

Un flujo de bits, por supuesto, es una señal binaria y el ruido en el flujo de bits se manifiesta como errores binarios en el flujo de bits. Considere una secuencia de\(7\text{ bits}\), idealmente\(\mathsf{1001110}\), con uno de los bits estando en error para que el flujo de bits recuperado sea\(\mathsf{1001010}\) donde\(1\text{ bit}\) in\(7\) está en error así\(\text{SIR}_{\text{eff}} = 7\).

5.6.2 Ganancia de codificación

Existen muchos tipos de esquemas de codificación de corrección de errores con algunos esquemas mejores para ciertos tipos de errores\(^{1}\). Generalizando, con cada bit de corrección de error adicional agregado a un flujo de bits de información para producir el flujo de bits de banda base, se puede corregir un error en el flujo de bits recuperado. Por lo tanto, la ganancia de procesamiento debida a la codificación (y a menudo llamada ganancia de codificación) al pasar de la banda base al flujo de bits de información es

\[\label{eq:2}G_{PC}=\frac{\text{SIR}_{\text{eff, }i}}{\text{SIR}_{\text{eff, }b}}=\frac{E_{b, i}/N_{o, i}}{E_{b, b}/N_{o, b}}=\frac{R_{b}}{R_{i}} \]

Esta es una ganancia de procesamiento bit a nivel de bits, ya que se aplica a los flujos de bits. La ganancia de codificación aquí no se limita a la codificación de corrección de errores ya que hay otros tipos de códigos llamados códigos de expansión que tienen una propiedad similar de proporcionar redundancia que se puede usar para eliminar errores. No los códigos son\(100\%\) efectivos. Sin embargo, la ecuación\(\eqref{eq:2}\) es la mejor medida simple de ganancia de procesamiento cuando solo se consideran flujos de bits. Proporciona la ganancia de codificación de un flujo de bits derivado de un segundo flujo de bits al que se ha utilizado la codificación para aleatorizar y aumentar la tasa de un flujo de bits e introducir así redundancia.

5.6.3 Ganancia de dispersión

La ecuación se\(\eqref{eq:2}\) puede reorganizar para que la información EBNO sea

\[\label{eq:3}\frac{E_{b, i}}{N_{o, i}}=G_{PC}\frac{E_{b, b}}{N_{o, b}} \]

La ganancia de procesamiento determinada en Ecuación\(\eqref{eq:2}\) se aplica a flujos de bits y no incluye el efecto de modulación. Una segunda forma de ganancia de procesamiento relaciona la SIR de la señal RF analógica, es decir\(\text{SIR}_{\text{RF}}\), con el EBNO del flujo de bits de banda base. Para incluir el efecto de modulación se reconoce que lo que se modula y transmite son símbolos y las transiciones de un símbolo a otro. Se denota la energía de un símbolo\(E_{s}\) y esta energía es compartida por el\(b\text{ bits}\) asociado con el símbolo. Así un bit de canal tendrá la energía\(E_{b, c} = E_{s}/b\). En radio digital, los niveles de potencia de las señales transmitidas se ajustan de manera que a lo sumo un bit de canal recibido puede estar en error por símbolo recibido. Por lo tanto, si el ruido recibido da como resultado un error de símbolo, afectará solo a un bit. Es decir, el ruido de símbolo será el mismo que el ruido de bit,\(N_{o, c} = N_{o}\) donde\(N_{o}\) está la energía de ruido en la duración de un símbolo. Por lo tanto, la SIR efectiva del flujo de bits del canal es

\[\label{eq:4}\text{SIR}_{\text{eff, }c}=\frac{E_{b, c}}{N_{o, c}}=\frac{E_{b, c}}{N_{o}}=\frac{E_{s}/b}{N_{o}} \]

El desarrollo se completa relacionando la energía de un símbolo con la energía de la señal de RF. Para la modulación PSK todos los símbolos tienen la misma energía. (La energía de cada símbolo no es la misma para formatos de modulación como QAM donde los símbolos tienen diferentes niveles de energía y se requiere una derivación más sofisticada que la proporcionada aquí). También la energía de ruido en la duración de un símbolo es la misma para todos los símbolos para todos los formatos de modulación. Así, el SIR efectivo de un símbolo es

\[\label{eq:5}\text{SIR}_{\text{RF}}=\frac{E_{s}}{N_{o}} \]

Así, la SIR efectiva del flujo de bits del canal es (combinando Ecuaciones\(\eqref{eq:4}\) y\(\eqref{eq:5}\),

\[\label{eq:6}\text{SIR}_{\text{eff, }c}=\frac{E_{b, c}}{N_{o, c}}=\frac{1}{b}\text{SIR}_{\text{RF}} \]

La ganancia de procesamiento que relaciona el EBNO del flujo de bits de banda base recuperado con la SIR de la señal de RF se puede definir como la ganancia de procesamiento debido a la expansión y modulación y esto a veces se llama solo la ganancia de expansión\(G_{PS}\). Se define aquí como la relación de la SIR efectiva del flujo de bits de banda base y la SIR de RF (y usando la ecuación\(\eqref{eq:6}\)):

\[\label{eq:7}G_{PS}=\frac{E_{b, b}/N_{o, b}}{\text{SIR}_{\text{RF}}}=\frac{1}{b}\frac{E_{b, b}/N_{o, b}}{\text{SIR}_{\text{eff, }c}}=\frac{1}{b}\frac{\text{SIR}_{\text{eff, }b}}{\text{SIR}_{\text{eff, }c}} \]

Esto se puede reorganizar para que el EBNO del flujo de bits de banda base sea

\[\label{eq:8}\frac{E_{b, b}}{N_{o, b}}=G_{PS}\text{SIR}_{\text{RF}} \]

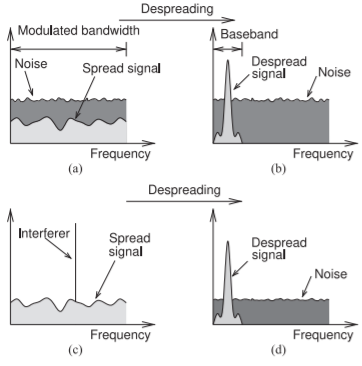
Figura\(\PageIndex{2}\): Aumento en la SNR obtenida al desensanchar una señal de espectro expandido: (a) el espectro de ruido y una señal de espectro expandido que tiene una potencia por debajo del nivel del ruido; (b) la señal desexpandida, donde la distribución de potencia del ruido no se cambia pero la señal desexpandida se limita a ancho de banda más estrecho llamado el ancho de banda de banda base; (c) una señal con un interferer de un solo tono; y (d) después de desensanchar donde la potencia del interferer se extendió a través del ancho de banda original.

La ecuación\(\eqref{eq:7}\) incluye la relación de los SIR efectivos de dos flujos de bits y esto se relacionó con las tasas de bits de los flujos de bits en la Ecuación\(\eqref{eq:2}\) donde el flujo de bits más rápido se codifica (o se propaga) para permitir la recuperación de errores. Usando el resultado en la ecuación\(\eqref{eq:2}\), la ecuación se\(\eqref{eq:7}\) puede escribir como

\[\label{eq:9}G_{PS}=\frac{1}{b}\frac{\text{SIR}_{\text{eff, }b}}{\text{SIR}_{\text{eff, }c}}=\frac{1}{b}\frac{R_{c}}{R_{b}} \]

Usando esto, el EBNO del flujo de bits de banda base es

\[\label{eq:10}\frac{E_{b, b}}{N_{o, b}}=\text{SIR}_{\text{eff, }b}=\frac{1}{b}\frac{R_{c}}{R_{b}}\text{SIR}_{\text{RF}}=\frac{1}{b}G_{PC}\text{SIR}_{\text{RF}} \]

Entonces el EBNO del flujo de bits de información es

\[\label{eq:11}\frac{E_{b, i}}{N_{o, i}}=G_{PC}\frac{E_{b, b}}{N_{o, b}}=G_{PC}G_{PS}\text{SIR}_{\text{RF}}=G_{P}\text{SIR}_{\text{RF}}=\frac{1}{b}\frac{R_{c}}{R_{i}}\text{SIR}_{\text{RF}} \]

donde la ganancia de procesamiento

\[\label{eq:12}G_{P}=G_{PC}G_{PS} \]

5.6.4 Ganancia de dispersión en términos de ancho de banda

La ganancia de ensanchamiento que resulta de la expansión de un flujo de bits de banda base en un transmisor y luego la despropagación en un receptor se ilustra gráficamente en la Figura\(\PageIndex{2}\). La señal modulada que se muestra en la Figura\(\PageIndex{2}\) (a) es la “señal ensanchada” que aquí tiene una densidad de potencia que está por debajo de la del ruido. Después de desensanchar toda la energía en la señal de RF modulada se correlaciona con el código de ensanchamiento (se extendió usando el código de ensanchamiento) y se colapsa a la señal desexpandida mostrada en la Figura\(\PageIndex{2}\) (b). Solo la señal correlacionada con el código de desensanchamiento se colapsa al ancho de banda base más pequeño. El ruido se reordena con la densidad espectral del ruido sin cambios de modo que la energía de ruido total en la banda base durante la duración de un bit de datos, es decir, el ruido en el ancho de banda de banda base\(B_{b}\), se reduce en gran medida por la relación entre el ancho de banda modulado y el ancho de banda de banda base.

En Ecuación\(\eqref{eq:9}\)\(R_{c}\) se relaciona con el ancho de banda Bm de la portadora modulada por la eficiencia de modulación como\(\eta_{c} = R_{c}/B_{m}\) (ver Ecuación (5.5.3)). También el ancho de banda mínimo de un flujo de bits de banda base con una tasa de bits\(R_{b}\) es el ancho de banda base\(B_{b} = R_{c}\). Entonces Ecuación\(\eqref{eq:9}\) se convierte

\[\label{eq:13}G_{PS}=\frac{\eta_{c}}{b}\frac{B_{m}}{B_{b}} \]

Idealmente para un esquema de modulación\(\eta_{c} = b\) para que

\[\label{eq:14}G_{PS,\text{ ideal}}=\frac{B_{m}}{B_{b}} \]

Para todos los esquemas de modulación que no sean BPSK donde\(\eta_{c}\) pueda estar muy cerca\(b\), la ganancia de propagación será menor que\(G_{PS,\text{ ideal}}\) como en la realidad\(\eta_{c} < b\), ver Tabla\(\PageIndex{1}\). Si se utilizan tanto la codificación de propagación como la corrección de errores, las dos ganancias de procesamiento en Ecuaciones\(\eqref{eq:2}\) y se\(\eqref{eq:13}\) pueden multiplicar.

5.6.5 Tasa de error de símbolo y tasa de error de bits

Con la modulación digital, los símbolos (es decir, grupos de bits) se transmiten en lugar de bits individuales. A medida que aumenta el orden de modulación, aumenta el número de símbolos y hay un margen menor entre los símbolos. Es decir, en un diagrama de constelación hay más símbolos y los símbolos están más cerca entre sí. Para los mismos niveles de señal y ruido, a medida que aumenta el orden de modulación, la probabilidad de un error de símbolo aumentará y así la tasa de error de símbolo (SER) aumenta. Sin embargo, la tasa de errores de bits (BER) aumenta más lentamente que la SER. Esto se debe a que si la SIR es lo suficientemente alta, los únicos errores posibles serán los errores del vecino más cercano (en un diagrama de constelación). Si hay al menos\(b\text{ bits}\) por símbolo la BER será menor que la tasa de error del símbolo por un factor de ya que los errores son\(b\) como máximo un bit por símbolo ya que el orden de modulación o el nivel de potencia de la señal se ajustan para asegurar esto. Si no es posible lograr un error máximo de un bit por error de símbolo, entonces se pierde la comunicación. El resto de esta sección trata este análisis de manera más matemática.

La discusión comienza con la SIR de la señal RF entrante. Mediante el muestreo de la señal de RF en momentos apropiados (determinados por la portadora recuperada) se obtienen símbolos discretos. La forma digital de SIR relaciona la energía de un símbolo\(E_{s}\),, con la energía de ruido e interferencia correspondiente al símbolo (el ruido y la interferencia en la duración del símbolo). La altura de la densidad espectral de ruido de doble cara se toma convencionalmente como\(N_{o}/2\), por lo que la potencia de ruido correspondiente a un símbolo es\(N_{o}\). Así [16, 17, 18]

\[\label{eq:15}\frac{E_{s}}{N_{o}}=\text{SIR} \]

El error en un sistema de comunicaciones modulado digitalmente se manifiesta primero como un error de símbolo que ocurre cuando un símbolo seleccionado en un receptor no es el símbolo transmitido. La probabilidad de un error de símbolo es una función de\(E_{s}/N_{o}\). Sin embargo, no siempre es posible desarrollar una expresión de forma cerrada que relacione las dos. Para un sistema BPSK se puede derivar. La probabilidad de

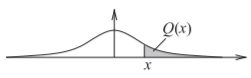
Figura\(\PageIndex{3}\): Función de distribución gaussiana que muestra la\(Q\) función como el área de la región sombreada.

un error de símbolo, el SER, es [16, p. 187]

\[\label{eq:16}\text{SER}_{\text{BPSK}}=\text{Pr}[\text{symbol error}]=\text{Pr}_{s}^{\text{BPSK}}=Q\left(\sqrt{\frac{2E_{s}}{N_{o}}}\right)=Q\left(\sqrt{2\cdot\text{SIR}}\right) \]

donde\(Q(x)\) se conoce como la\(Q\) función [16] y es la integral de la cola de la función de densidad gaussiana (ver Figura\(\PageIndex{3}\)). Se puede expresar en términos de la función de error\(\text{erf}(x)\) y función complementaria\(\text{erfc}(x)\) [16, página 63]:

\[\label{eq:17}Q(x)=\frac{1}{2}\text{erfc}\left(\frac{x}{\sqrt{2}}\right)=\frac{1}{2}\left[1-\text{erf}\left(\frac{x}{\sqrt{2}}\right)\right] \]

Para\(M\text{-PSK}\) [16, página 191] el SER es

\[\label{eq:18}\text{SER}_{M\text{-PSK}}=\text{Pr}_{s}^{M\text{-PSK}}\approx 2Q\left[\sqrt{\frac{2E_{s}}{N_{o}}}\sin\left(\frac{\pi}{M}\right)\right] \]

donde\(M\) es el número de símbolos (por ejemplo, para 8-QPSK\(M = 8\)). Para ver el efecto de la modulación de orden superior (es decir, superior\(M\)) considere la Ecuación\(\eqref{eq:18}\). A medida que aumenta el orden de modulación,\(M\) aumenta, y el argumento de\(Q\) reduce, aumentando así SER.

La SIR por bit se obtiene después de señalar que cada símbolo puede representar varios bits. Con una constelación uniforme y el mismo número de bits por símbolo,\(b\), la energía de la señal recibida por bit es

\[\label{eq:19}E_{b}=E_{s}/b,\qquad b=\log_{2}M \]

y

\[\label{eq:20}M=2^{b} \]

Para una SIR alta, un error de símbolo es la selección errónea de un símbolo vecino más cercano por parte del receptor. Entonces, con el mapeo de código Gray (también llamado mapeo Gray), tal error de símbolo da como resultado que solo un bit esté en error. Así, la probabilidad de un error de bit, el BER, es

\[\label{eq:21}\text{Pr}[\text{bit error}]=\text{Pr}_{b}=\frac{1}{b}\text{Pr}_{s} \]

Los resultados finales son las probabilidades de error de bit para BPSK y M-PSK [16, página 193]:

\[\begin{align}\label{eq:22}\text{BER}|_{\text{BPSK}}&=\text{Pr}_{b\text{, BPSK}}=Q\left(\sqrt{2E_{s}/N_{o}}\right) =Q\left(\sqrt{2\cdot\text{SIR}}\right) \\ \text{BER}|_{M\text{-PSK}}&=\text{Pr}_{b,M\text{-PSK}}=\frac{2}{b}Q\left[\sqrt{2E_{s}/N_{o}}\sin\left(\frac{\pi}{M}\right)\right] \\ \label{eq:23} &=\frac{2}{b}Q\left[\sqrt{2\cdot\text{SIR}}\sin\left(\frac{\pi}{M}\right)\right]\end{align} \]

Así, para la misma SIR la probabilidad de errores de bit, la BER, crece con modulación de orden superior (es decir, mayor\(M\)), pero no tan rápido como SER. Al mismo tiempo aumenta el número de bits transmitidos. Estos bits adicionales se utilizan para incrustar códigos de corrección de errores. La ganancia neta en el rendimiento puede ser tremenda siempre que la SIR sea lo suficientemente alta.

Ejemplo\(\PageIndex{1}\): Symbol Error Rate

Calcular el SER y BER para QPSK y 8-PSK si el SIR es\(10\text{ dB}\).

Solución

SER se encuentra evaluando la Ecuación\(\eqref{eq:18}\). Para\(\text{SIR} = 10\text{ dB},\: E_{s}/N_{o}= 10^{(\text{SIR}_{\text{dB}}/10)} = 10\). Para QPSK,\(M = 4\) y\(b = 2\), y el SER es

\[\begin{align}\text{SER}_{\text{QPSK}}&=\text{Pr}_{s}^{M\text{-PSK}}\approx 2Q\left(\sqrt{\frac{2E_{s}}{N_{o}}}\sin\left(\frac{\pi}{M}\right)\right)=2Q\left[\sqrt{20}\sin\left(\frac{\pi}{4}\right)\right] \nonumber \\ \label{eq:24} &=2Q(3.162)=\left[1-\text{erf}(3.162/\sqrt{2})\right]=0.001565\end{align} \]

Para 8-PSK,\(M = 8\) y\(b = 3\), y el SER es

\[\begin{align}\text{SER}_{8\text{-PSK}}&=\text{Pr}_{s}^{M\text{-PSK}}\approx 2Q\left[\sqrt{\frac{2E_{s}}{N_{o}}}\sin\left(\frac{\pi}{M}\right)\right]=2Q\left(\sqrt{20}\sin\left(\frac{\pi}{8}\right)\right)\nonumber \\ \label{eq:25}&=2Q(1.711)=0.08701\end{align} \]

Los BER correspondientes son

\[\label{eq:26}\text{BER}_{\text{QPSK}}=\frac{1}{2}\text{SER}_{\text{QPSK}}=0.000783\quad\text{and}\quad\text{BER}_{8\text{-PSK}}=\frac{1}{3}\text{SER}_{8\text{-PSK}}=0.0290 \]

5.6.6 Resumen

Las fórmulas para procesar ganancia desarrolladas anteriormente son solo aproximadas ya que se hicieron muchas simplificaciones. Una suposición es que la codificación de corrección de errores es bits completamente aleatorios pero en la práctica hay muchos códigos de corrección de errores que abordan tipos particulares de errores. El objetivo de la codificación de corrección de errores es recuperarse de errores no necesariamente para lograr ganancia de procesamiento.

Otra advertencia a las fórmulas de ganancia de procesamiento desarrolladas aquí es que consideró que la energía de un símbolo era la misma para todos los símbolos. Si bien esto es cierto para la modulación PSK, no es cierto para todos los formatos de modulación. Se pone un esfuerzo considerable en desarrollar mejores estimaciones que capten la esencia de la ganancia de procesamiento pero de una manera más rigurosa. Aún así, las fórmulas simples proporcionan la información requerida sobre el efecto del uso de códigos de corrección de errores y propagación.

En 2G la ganancia de procesamiento de radio celular se logra usando códigos de corrección de errores solos y no se usa un código de ensanchamiento separado. Así, en 2G los bits de banda base son también los bits de canal utilizados directamente en la modulación de la portadora de RF. Los bits adicionales proporcionan redundancia y la capacidad de recuperarse de algunos errores resultantes del ruido. En 3G se utilizan códigos de ensanchamiento así como códigos de corrección de errores. Un código de dispersión aumenta en gran medida la tasa de bits del flujo de bits del canal por encima de la del flujo de bits de banda base y el ancho de banda de la portadora modulada es mucho mayor que el necesario para transmitir el flujo de bits de banda base. Generalmente, los códigos de corrección de errores no aumentan la tasa de bits en más de un factor de\(2\). Así, en 3G la ganancia de procesamiento conseguida con los códigos de corrección de errores es casi insignificante en comparación con

Descripción	Definición	Fórmula	Ecuación
Ganancia de codificación, ganancia de procesamiento de codificación de corrección de errores. Calculado para flujos de bits.	\(G_{PC}=\frac{E_{b, i}/N_{o, i}}{E_{b, b}/N_{o, b}}\)	\(G_{PC}=\frac{R_{b}}{R_{i}}\)	\(\eqref{eq:2}\)
Ganancia de procesamiento del ensanchamiento calculada sobre una base de flujo de bits	\(G_{PS}=\frac{E_{b, c}/N_{o, c}}{E_{b, b}/N_{o, b}}\)	\(G_{PS}=\frac{1}{b}\frac{R_{c}}{R_{b}}\)	\(\eqref{eq:9}\)
Procesamiento de ganancia de propagación en términos de ancho de banda.	\(G_{PS}=\frac{E_{b, b}/N_{o, b}}{\text{SIR}_{\text{RF}}}\)	\(G_{PS}=\frac{\eta_{c}}{b}\frac{B_{m}}{B_{b}}\)	\(\eqref{eq:13}\)
Ganancia de procesamiento	\(G_{P}=\frac{E_{b, c}/N_{o, c}}{E_{b, i}/N_{o, i}}\)	\(G_{P}=G_{PC}G_{PS}\)	\(\eqref{eq:12}\)
EBNO	\(E_{b, i}/N_{b, i}\)	\(E_{b, i}/N_{b, i}=G_{P}\text{SIR}_{\text{RF}}\)	\(\eqref{eq:8}\)

Tabla\(\PageIndex{1}\): Definiciones de ganancia de procesamiento. \(R_{i}\)es la tasa de bits de información,\(R_{b} > R_{i}\) es la tasa de bits de banda base después de la codificación de corrección de errores del flujo de bits de información, y\(R_{c} > R_{b}\) es la tasa de bits de canal después de expandir el flujo de bits de banda base Se hace referencia al flujo de bits\(x\) ésimo con\(x = i, b,\) o\(c\) que indica la información, la banda base o los flujos de bits de canal respectivamente. \(B_{b, x}\)es la energía de un bit en el flujo de bits\(x\) th, y\(N_{o, x}\) es la energía de ruido equivalente correspondiente a un bit en el\(x\) th flujo de bits. \(E_{s}\)es la energía de un símbolo con\(b\text{ bits}\) por símbolo. \(B_{m}\)es el ancho de banda de la portadora modulada y\(B_{b}\) es el ancho de banda de la señal de banda base.

que se obtiene de la propagación de la señal.

En 4G y 5G la codificación de corrección de errores también proporciona propagación y no hay un código de propagación separado. Los sistemas 4G y 5G tienen una gran complejidad.

Un resumen de los resultados clave para la ganancia de procesamiento se da en la Tabla\(\PageIndex{1}\).

Ejemplo\(\PageIndex{2}\): Processing Gain

Se está investigando un nuevo sistema de comunicación para enviar datos a una impresora. El sistema utilizará modulación GMSK y será un canal con\(10\text{ MHz}\) ancho de banda y la tasa de bits de banda base\(1\text{ Mbit/s}\). El formato de modulación dará como resultado un espectro que distribuye (es decir, propaga) la potencia casi uniformemente sobre el\(10\text{ MHz}\) ancho de banda.

1. ¿Cuál es la ganancia de procesamiento?
   La forma más eficiente de propagar la señal a través\(10\text{ MHz}\) del ancho de banda disponible es usar una combinación de corrección de errores y propagación. Haciendo referencia a la Tabla 2.9.1, GMSK tiene una eficiencia\(\eta_{c}\) de modulación de\(1.354\text{ bit/s/Hz}\), de manera que la tasa de bits del canal\(R_{c} = 13.54\text{ Mbit/s}\). Cada símbolo en GMSK representa dos bits así\(b = 2\). Se utilizará la tasa de bits de información\(R_{i} = 1\text{ Mbit/s}\) y así la codificación\(12.54\text{ Mbit/s}\) a la velocidad de y\(R_{b} = (R_{i} + 12.54\text{ Mbit/s}) = 13.54\text{ Mbit/s}\).
   Hay dos ganancias de procesamiento. La ganancia de codificación se determina usando la Ecuación\(\eqref{eq:2}\):
   \[G_{PC}=\frac{R_{b}}{R_{i}}=\frac{13.54\text{ Mbit/s}}{1\text{ Mbit/s}}=13.54=11.31\text{ dB}\nonumber \]
   La ganancia de dispersión, usando Ecuación\(\eqref{eq:9}\), es
   \[G_{PS}=\frac{1}{b}\frac{R_{c}}{R_{b}}=\frac{1}{2}\frac{1\text{ Mbit/s}}{1\text{ Mbit/s}}=0.5=-3\text{ dB}\nonumber \]
   Así la ganancia de procesamiento
   \[G_{P}=G_{PC}G_{PS}=6.77=8.31\text{ dB}\nonumber \]
   Otra forma de calcular la ganancia de ensanchamiento es considerar el ancho de banda modulado,\(B_{m} = 10\text{ MHz}\) y el ancho de banda de banda base\(B_{b} = 1\text{ MHz}\) (tomado para ser numéricamente igual a\(R_{b}\)). La ganancia de procesamiento debido a la dispersión, de la ecuación\(\eqref{eq:13}\):
   \[G_{PS}=\frac{\eta_{c}}{b}\frac{B_{m}}{B_{b}}=\frac{1.354}{2}\frac{10\text{ MHz}}{1\text{ MHz}}=6.770=8.31\text{ dB}\nonumber \]
2. Si el RF SIR recibido es\(\text{SIR}_{\text{RF}} = 6\text{ dB}\), ¿cuál es el SIR efectivo del sistema (o\(E_{b}/N_{o}\)) después del procesador de señal digital?
   \[\text{Effective SIR}=\frac{E_{b, i}}{N_{o, i}}=G_{P}\text{SIR}_{\text{RF}}=8.31\text{ dB}+6\text{ dB}=14.32\text{ dB}\nonumber \]

Ejemplo\(\PageIndex{3}\): Signal-to-Interference Ratio

En la salida de una antena receptora, el nivel de señales interferentes es\(1\text{ pW}\), el nivel de ruido de fondo es\(500\text{ fW}\), y el nivel de la señal deseada es\(4\text{ pW}\).

1. ¿Qué es el SIR? Tenga en cuenta que SIR incluye el efecto de la señal, la interferencia y el ruido.
2. Si la ganancia de procesamiento es\(20\text{ dB}\) y 16-QAM es el esquema de modulación utilizado, ¿cuál es el sistema efectivo SIR, es decir, cuál es la energía de la señal en un bit frente a la energía de ruido en la duración del bit (es decir,\(E_{b}/N_{o}\))?

Solución

1. Señal\(P_{I} = 1\text{ pW},\text{ noise signal }P_{N} = 500\text{ fW}\) interferente y señal\(P_{S} = 4\text{ pW}\).
   \[\begin{aligned}\text{SIR}_{\text{RF}}&=P_{S}/(P_{I}+P_{N})\nonumber \\ &=4\text{ pW}(1\text{ pW}+0.5\text{ pW})=4/1.5 =2.667=4.26\text{ dB}\nonumber\end{aligned} \nonumber \]
2. Procesando ganancia\(G_{P} = 20\text{ dB}\) así, a partir de la ecuación\(\eqref{eq:11}\)
   \[\text{Effective SIR}=\frac{E_{b, i}}{N_{o}}=G_{P}\cdot\text{SIR}_{\text{RF}}=20\text{ dB}+4.26\text{ dB}=24.26\text{ dB}\nonumber \]

Notas al pie

[1] Los códigos de error utilizados en la radio celular son códigos de corrección de errores hacia delante (FEC) también llamados códigos de canal. Hay muchos códigos FEC ampliamente categorizados como códigos de bloque (porque funcionan en bloques de datos) o códigos de convolución (porque funcionan en flujos de bits de longitud arbitraria). Los diversos códigos FEC utilizan diferentes modelos (es decir, suposiciones) sobre los tipos de errores encontrados. La selección del código FEC a usar es una elección de diseño basada en la potencia de cálculo disponible y la naturaleza de los errores, por ejemplo, cadenas de errores aleatorias o largas.