5.8: Discusión Avanzada del Ruido del Oscilador

En esta sección se presenta una discusión sobre el ruido del oscilador, y particularmente el rápido aumento del ruido de fase cerca de la portadora. El ruido se puede dividir en componentes de ruido de amplitud y fase. La saturación no lineal de un oscilador suprime el ruido de amplitud, por lo que solo el ruido de fase es motivo de preocupación. Si bien generalmente se asocia con osciladores, el ruido de fase también se agrega a una señal por un amplificador.

No hay consenso en cuanto a los orígenes del ruido de fase cercano a la portadora. Esta sección comienza con observaciones del ruido del oscilador en el dominio de la frecuencia y en el dominio del tiempo. Luego se presentan tres teorías del exceso de ruido del oscilador, la teoría de Leeson, el modelo lineal invariante en el tiempo y el modelo de mapa caótico.

No tener un modelo completo del origen físico del ruido de fase significa que un simulador no puede predecir de manera confiable el ruido de fase de un oscilador. También diseñar un oscilador con buen rendimiento de ruido de fase actualmente se basa en gran medida en la experiencia y proyecciones basadas en lo que ha sido logrado por un diseñador anteriormente.

5.8.1 Observaciones del ruido del oscilador en el dominio de la frecuencia

El ruido más desconcertante observado con los osciladores es el ruido observado a una pequeña desviación de frecuencia con respecto a la portadora (es decir, la señal de oscilación promedio). Para desarrollar una apreciación por la amplitud de las observaciones, se considerarán las señales producidas por varios osciladores diferentes. Primero, Figura\(\PageIndex{2}\)

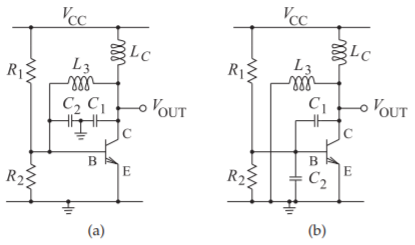
Figura\(\PageIndex{1}\): Emisor común BJT Colpitts osciladores: (a) configuración con una red de retroalimentación entre el colector y la base del transistor; y (b) configuración alternativa.

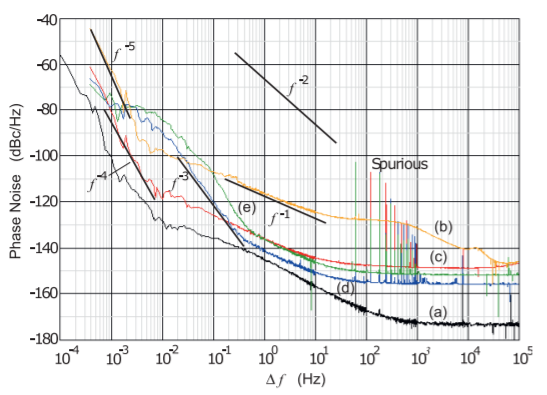
Figura\(\PageIndex{2}\): Ruido de fase medido de osciladores de baja frecuencia: (a) piso de ruido del instrumento; (b) amplificador de distribución de frecuencia HP 5087A en\(5\text{ MHz}\) (utilizado para accionar la entrada de referencia externa de varios instrumentos de prueba usando un solo oscilador de alta calidad); (c) distribución de frecuencia TAD-1 amplificador a\(10\text{ MHz}\); (d) amplificador de distribución de frecuencia TAD-1 a\(5\text{ MHz}\); (e) Amplificador de distribución de frecuencia Spectracom 8140T a 10 MHz. Cinco regiones de ruido de fase se identifican como\(f^{−5},\: f^{−4},\: f^{−3},\: f^{−1}\), y ruido blanco. Las señales espurias están relacionadas con armónicos inyectados de la red\(60\text{ Hz}\) eléctrica. Usado con permiso de John Ackermann [23].

es una gráfica del ruido de fase observado en la salida de varios osciladores y amplificadores que operan en\(5\text{ MHz}\) y\(10\text{ MHz}\). La curva (a) es el piso de ruido del instrumento de medición de ruido y se observan tonos espurios en múltiplos de\(60\text{ Hz}\), la frecuencia de la red eléctrica. Las curvas (b), (c), (d) y (e) muestran ruido de fase que varía en segmentos de línea recta. Al ser una gráfica log-log, estas curvas muestran ruido de fase que varía como\(f^{−5},\: f^{−4},\: f^{−3},\: f^{−1}\), y\(f^{0}\). Ninguna de las gráficas de ruido de fase aquí muestra una región con\(f^{−2}\) dependencia, aunque esto se observa con otros osciladores.

Otro oscilador a considerar es el circuito VCO mostrado en la Figura\(\PageIndex{3}\) [24]. Se trata de un\(50\text{ MHz}\) VCO con un varactor semiconductor siendo el elemento variable con una capacitancia de polarización cero de\(100\text{ pF}\). La capacitancia del varactor es controlada por el voltaje,\(V_{b}\). Con\(V_{b} = 0\text{ V}\), se observó el ruido de fase mostrado en\(\PageIndex{4}\) la Figura. Las distintas regiones de ruido de fase tienen dependencias de frecuencia de\(f^{0},\: f^{−1},\: f^{−2}\), y\(f^{−3}\). El ruido de fase de este oscilador se traza nuevamente en la Figura\(\PageIndex{5}\) para tres tensiones de polarización de varactor diferentes. Las características del ruido de fase del oscilador cambian a pesar de que las fuentes físicas subyacentes de ruido no cambian (por supuesto). La curva (a), con\(V_{b} = 6\text{ V}\), y la curva (b), con\(V_{b} = 0\text{ V}\), tienen una\(f^{−1}\) región alrededor\(20\text{ kHz}\) (ver Figura\(\PageIndex{4}\) para más detalles), pero la\(f^{−1}\) región no se observa en la Curva (c) donde\(V_{b} = 18\text{ V}\). Una interpretación es que las frecuencias de cruce han cambiado. Entonces, lo que es particularmente interesante aquí es

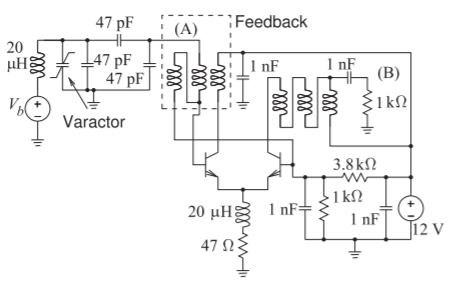
Figura\(\PageIndex{3}\): Esquema VCO sintonizado por Varactor, de [24].

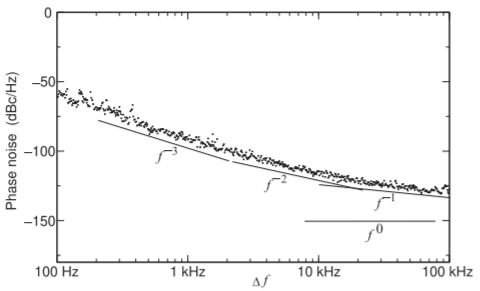
Figura\(\PageIndex{4}\): Ruido de fase medido de un VCO basado en varactor\(50\text{ MHz}\) BJT con el varactor sesgado a\(0\text{ V}\) [25, 26]. Las regiones de ruido trifásico se identifican como\(f^{−3}\) (que tienen una pendiente de\(−9\text{ dB}\) /octava),\(f^{−2}\) (que tienen una pendiente de\(−6\text{ dB}\) /octava) y\(f^{−1}\) (que tienen una pendiente de\(−3\text{ dB}\) /octava).

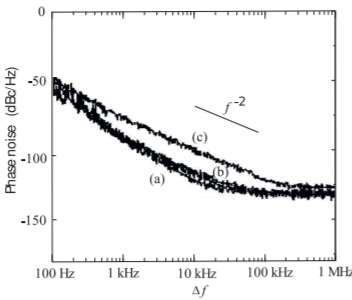
Figura\(\PageIndex{5}\): Ruido de fase medido de un VCO basado en varactor\(50\text{ MHz}\) BJT a tres tensiones de polarización de varactor: (a)\(6\text{ V}\); (b)\(0\text{ V}\); y (c)\(18\text{ V}\) [25]. El voltaje de ruptura del varactor es\(30\text{ V}\) Curva (b) también se graficó en la Figura\(\PageIndex{4}\).

que la misma fuente física de ruido puede manifestarse de manera bastante diferente en la salida de un oscilador cuando se cambia la polarización del circuito.

El tercer ejemplo de ruido de fase es para un oscilador de\(2.4\text{ GHz}\) potencia que tiene el espectro de salida mostrado en la Figura\(\PageIndex{6}\) con regiones que tienen dependencias de\(f^{−3}\) y\(f^{−0}\), pero nada en el medio. (El ligero aumento en la densidad espectral de potencia de ruido en el\(40\text{ kHz}\) desplazamiento se debe a la dinámica de los osciladores

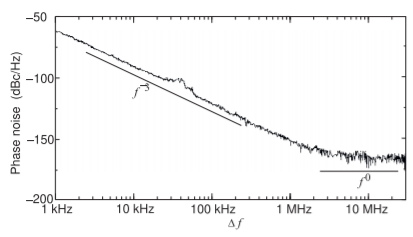
Figura\(\PageIndex{6}\): Ruido de fase de un oscilador de\(2.4\text{ GHz}\) potencia con una potencia de salida de\(34.5\text{ dBm}\) [27, p. 323]. Las regiones de ruido de dos fases se identifican como\(f^{−3}\) (que tienen una pendiente de\(−9\text{ dB}\) /octava) y ruido blanco (con una\(f^{0}\) dependencia).

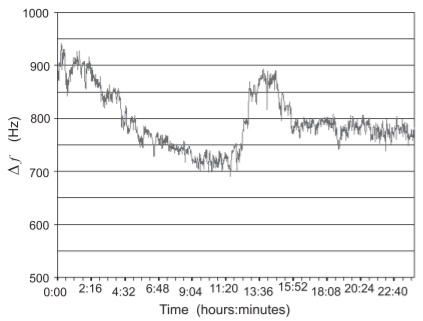
Figura\(\PageIndex{7}\): Estabilidad a largo plazo de un\(10\text{ GHz}\) oscilador medida en un intervalo de una\(24\) hora después de estar encendido por\(3\) semanas. Usado con permiso de John Ackermann [23].

bucle de retroalimentación.) Finalmente, el\(5\text{ GHz}\) oscilador considerado en la Sección 5.6 tiene\(f^{−3}\) y regiones de ruido de\(f^{−2}\) fase (ver Figura 5.6.15).

Entonces se observa todo el rango de dependencias de ruido de fase en el desplazamiento de frecuencia, pero la observación universal es que la dependencia de la densidad espectral de potencia de ruido es a una potencia entera no positiva de frecuencia (es decir,\(f^{−n},\: n = 0, 1,\ldots \)).

5.8.2 Observaciones del ruido del oscilador en el dominio del tiempo

Una caracterización importante del ruido en el dominio del tiempo se conoce como ruido de caminata aleatoria. Un ejemplo de esto es la variación de la frecuencia de oscilación a lo largo de un largo período de tiempo. La estabilidad a largo plazo de un\(10\text{ GHz}\) oscilador se muestra en la Figura\(\PageIndex{7}\). Este ruido no puede caracterizarse en el dominio de la frecuencia y en su lugar se describe por su varianza Allan\(\sigma_{y}^{2}(\tau )\), o desviación Allan\(\sigma_{y}(\tau ) =\sqrt{\sigma_{y}^{2}(\tau)}\), definida de la siguiente manera.

Si la frecuencia medida en el tiempo\(t\) es\(f(t)\) y la frecuencia de oscilación nominal es\(f_{n}\), entonces la frecuencia fraccionaria en el tiempo\(t\) se define como

\[\label{eq:1}y(t)=\frac{f(t)-f_{n}}{f_{n}} \]

Luego, la frecuencia fraccional promedio en un intervalo de tiempo de observación\(\tau\) se define como

\[\label{eq:2}\overline{y}(t,\tau )=\frac{1}{\tau}\int_{0}^{\tau}y(t+t_{v})dt_{v} \]

Esto lleva a la definición de la varianza Allan como

\[\label{eq:3}\sigma_{y}^{2}(\tau)=\frac{1}{2}\left<\overline{y}_{n+1}-\overline{y}_{n}\right> \]

donde\(\tau\) es el periodo de observación y\(\overline{y}_{n}\) es el\(n\) th promedio de frecuencia fraccional a lo largo del intervalo de tiempo\(\tau\). Tenga en cuenta que no hay tiempo muerto entre los intervalos de tiempo de medición\(n\)\((n + 1)\) th y th.

El paseo aleatorio que se muestra en la Figura\(\PageIndex{7}\) es una pista importante para desentrañar el ruido de parpadeo. La figura\(\PageIndex{7}\) muestra la memoria a largo plazo y aquí se muestra que hay memoria a lo largo de varias horas. Incluso en escalas de tiempo más pequeñas, la caminata aleatoria es evidente y existe una propiedad autosimilar, el sello distintivo del comportamiento caótico. ¿Podría este efecto de caminata aleatoria y\(1/f\) ruido surgir del mismo proceso físico? Lo más probable, pero no hay teoría aceptada.

5.8.3 Exceso de ruido del oscilador: el efecto Leeson y el ruido de parpadeo

Como se ve en las Figuras\(\PageIndex{2}\) a\(\PageIndex{6}\), los osciladores tienen ruido que aumenta a medida que disminuye el desplazamiento\(\Delta f\), a partir de la frecuencia media de oscilación. Este ruido tiene regiones separables donde el ruido varía como\(\Delta f^{n}\), donde\(n\) es un número entero que va desde\(0\) hasta\(−5\). Hay regiones de transición entre estos estados discretos, pero no hay una región donde\(n\) haya un número fraccionario. No todos los estados discretos se observan porque, presumiblemente, o bien las frecuencias de cruce han cambiado de orden, o el desplazamiento de frecuencia\(\Delta f\), no fue lo suficientemente bajo.

En 1966 Leeson [28] examinó el efecto de la retroalimentación sobre el ruido en los osciladores (ver Figura 5.2.1). El mecanismo de ruido de fase tratado por este análisis se denomina ahora efecto Leeson. Leeson demostró que el ruido de fase blanca y el ruido de parpadeo blanco (blanco aquí significa independiente de la frecuencia) del amplificador en el bucle de retroalimentación se traducen en ruido en la señal de oscilación con dependencias de la ley de potencia de\(f^{−2}\), llamado ruido de frecuencia blanca, y\(f^{−3}\), llamado ruido de frecuencia de parpadeo, respectivamente. Estas fueron las formas dominantes de ruido “no blancas” observadas en su tiempo. Sin embargo, su análisis no predijo el nivel del ruido con precisión y a veces estaba apagado por un orden de magnitud.

Aquí se resume brevemente el efecto Leeson. En primer lugar, se observó que casi todos los sistemas físicos tienen fluctuaciones que varían como\(1/f\) a bajas frecuencias. Esto incluye dispositivos eléctricos como el amplificador en un bucle de retroalimentación del oscilador. Esto conduce a una amplitud igual de ruido de fase y amplitud superpuesta a la oscilación. Dado que el ruido es pequeño, las fluctuaciones de amplitud son suprimidas por la saturación del dispositivo activo de manera que el único ruido observado en buenos diseños es el ruido de fase. Leeson determinó que el ruido de fase del oscilador tiene una región con\(\Delta f^{−3}\) dependencia que se debe al\(f^{−1}\) ruido de baja frecuencia (es decir, alrededor de CC), una\(\Delta f^{−2}\) región debida al ruido blanco en el ancho de banda del circuito del tanque del oscilador, y también una región de ruido blanco fuera del ancho de banda del tanque circuito. La base para el desarrollo del modelo de ruido de fase del oscilador de Leeson se muestra en la Figura\(\PageIndex{8}\). Matemáticamente [28],

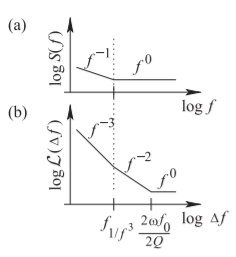
Figura\(\PageIndex{8}\): Derivación de los espectros de ruido del oscilador: (a) los espectros de ruido de un material electrónico con ruido que aumenta a medida que disminuye la frecuencia; y (b) los espectros de ruido cercanos a la frecuencia de oscilación de un oscilador.

\[\label{eq:4}\mathcal{L}(\Delta f)=\mathcal{L}(\Delta\omega)=\frac{2FkT}{P_{0}}\left[1+\left(\frac{f_{0}}{2Q\Delta f}\right)^{2}\right] \]

donde\(Q\) es el\(Q\) factor cargado del circuito tanque del oscilador y\(F\) es un factor empírico. \(\mathcal{L}\)tiene las unidades de\(\text{radians}^{2}\text{/Hz}\), o en decibelios,

\[\label{eq:5}\mathcal{L}|_{\text{dB}}(\Delta f)=10\log\left\{\frac{2FkT}{P_{0}}\left[1+\left(\frac{f_{0}}{2Q\Delta f}\right)^{2}\right]\right\} \]

que tenga las unidades de\(\text{dB/Hz}\) o más usualmente expresadas como” decibelios por debajo del portador” del poder\(P_{0}\), o\(\text{dBc/Hz}\). Esta es la potencia a un desplazamiento especificado tal como el ruido de fase de un\(5.05\text{ GHz}\) oscilador en un desplazamiento de\(1\text{ MHz}\) y con una potencia de salida de\(0\text{ dBm}\) ser\(−130\text{ dBc/Hz}\) [19].

La derivación de las características del ruido del oscilador a partir de los primeros principios, lo que derivó en Ecuaciones\(\eqref{eq:4}\) y\(\eqref{eq:5}\), predice niveles de ruido que son muy inferiores a los observados en la práctica [29, 30]. Además, la predicción inherente a la Ecuación\(\eqref{eq:4}\) es que al aumentar el\(Q\) del circuito del tanque se reducirá el nivel de ruido. Sin embargo, esto no siempre se obtiene en la práctica. Una complicación adicional es que la ecuación no\(\eqref{eq:4}\) proporciona ningún mecanismo para la generación\(1/(\Delta f)\) y el\(1/(\Delta f)^{3}\) ruido en el espectro de ruido de fase del oscilador. Una modificación adhoc de la ecuación\(\eqref{eq:4}\) explica esto:

\[\label{eq:6}\mathcal{L}(\Delta f)=\frac{2FkT}{P_{0}}\left[1+\left(\frac{f_{0}}{2Q\Delta f}\right)^{2}\right]\left(1+\frac{f_{c-3}}{|\Delta f|}\right) \]

Dada la insuficiencia de este modelo es igual de bien utilizar

\[\label{eq:7}\mathcal{L}(\Delta f)=\sum_{i=0}^{-5}b_{i}f_{i}^{n} \]

donde se extraen los\(b_{i}\) coeficientes de las mediciones.

El efecto Leeson se puede afirmar como ruido de fase del oscilador que se convierte en ruido blanco ascendente alrededor de CC.

5.8.4 Exceso de ruido del oscilador: Modelo lineal con variante de tiempo

El modelo de efecto Leeson descrito en la subsección anterior utiliza un modelo lineal invariable en el tiempo del oscilador y no considera la conversión descendente de ruido de frecuencias cercanas a armónicos. El modelo lineal de variante temporal, también llamado modelo Hajimiri y Lee, incorpora estos mecanismos de conversión de orden superior [31].

El ruido inyectado en un oscilador tiene un impacto diferente dependiendo de si se inyecta en el pico de la señal oscilante o en los cruces por cero. El ruido inyectado en los picos de la señal oscilante se apaga por el efecto de saturación del dispositivo activo en el oscilador. Sin embargo, el ruido en o cerca de los cruces por cero de la forma de onda introduce ruido de fase y fluctuación. Este efecto sobre el ruido de fase puede describirse mediante una función de sensibilidad al impulso [31]. Considere un impulso inyectado en fase\(x =\omega_{0}t\), luego la respuesta de impulso en el dominio del tiempo es

\[\label{eq:8}h_{\phi}(t,\tau )=\frac{\Gamma(\omega_{0}t)}{q_{\text{max}}}u(t-\tau ) \]

donde\(\Gamma (\: )\) está la función de sensibilidad al impulso,\(q_{\text{max}}\) es el desplazamiento de carga máximo en el condensador que forma el circuito del tanque,\(t\) es el tiempo de observación, y\(\tau\) es el tiempo de la excitación. El exceso de fase del oscilador (la fase adicional inducida sobre la fase de la portadora) es

\[\label{eq:9}\phi (t)=\frac{1}{q_{\text{max}}}\int_{-∞}^{t}\Gamma(\omega_{0}t)i(\tau )d\tau \]

donde\(i(\tau )\) esta la corriente de ruido inyectada en el oscilador.

\(\Gamma(\: )\)se puede derivar aproximadamente para algunos osciladores como el oscilador CMOS LC en [32], donde se demostró que la función de sensibilidad al impulso puede expresarse como una serie de Fourier con un componente fundamental correspondiente a la frecuencia de oscilación. El exceso de fase en los cruces por cero del oscilador es

\[\label{eq:10}\phi (t)=\frac{1}{q_{\text{max}}}\left[c_{0}\int_{-∞}^{t}i(\tau )d\tau +\sum_{m=1}^{∞}c_{m}\int_{-∞}^{t}i(\tau)\cos(n\omega_{0}\tau )d\tau\right] \]

donde\(c_{m}\) están los coeficientes de la serie de Fourier. El primer término con el\(c_{0}\) coeficiente indica ruido que se convierte ascendentemente desde la banda base, mientras que el término en la suma es la contribución al ruido de fase del oscilador debido a la conversión descendente de ruido cerca de las frecuencias armónicas. Con la suposición de que el ruido en los armónicos es ruido blanco con corriente media cuadrada\(\overline{i_{n}^{2}}\), entonces la densidad espectral del ruido es [32, 33]

\[\label{eq:11}\mathcal{L}(\Delta\omega)=10\log\left(\frac{\overline{i}_{n}^{2}}{\Delta f}\frac{\sum_{m=0}^{∞}c_{m}^{2}}{4q_{\text{max}}^{2}\Delta\omega^{2}}\right) \]

Aquí\(\Delta f = 1\text{ Hz}\) para el ruido en un\(1\text{ Hz}\) ancho de banda y\(\Delta\omega\) es la frecuencia de desplazamiento del radián. Por lo tanto, el ruido blanco en los armónicos se convierte descendentemente en\(f^{−2}\) ruido a la frecuencia de oscilación, y el\(f^{−1}\) ruido en la banda base se convierte ascendentemente en\(f^{−3}\) ruido a la frecuencia de oscilación.

El modelo de variante de tiempo proporciona una descripción más rica del ruido de fase en una señal oscilante que el modelo Leeson, pero no describe\(f^{−1}\), o\(f^{−n},\: n> 3\), el ruido que se observa con los osciladores.

Así, el modelo de Hajimiri y Lee se relaciona con la conversión descendente del ruido blanco en los armónicos de la frecuencia de oscilación al ruido de la portadora cercana, que se suma al modelo de Leeson de ruido blanco cercano a CC convertido ascendentemente. Los modelos Hajimiri y Lee, y Leeson de ruido de fase llevaron a los diseñadores a desarrollar osciladores de microondas con un diseño de fase significativamente menor, pero sigue habiendo un ruido de fase cercano a la portadora apreciable.

5.8.5 Exceso de ruido del oscilador: mapas caóticos y ruido de parpadeo

Si bien no está firmemente establecido, es posible que el ruido de parpadeo se origine a partir de dinámicas no lineales y caos [25, 26, 34, 35, 36, 37, 38, 39, 40, 41]. En este modelo el ruido de parpadeo deriva de un proceso no lineal con retroalimentación retardada. El fundamento matemático está bien establecido [42], describiendo un fenómeno llamado intermitencia [43] que ocurre cuando un proceso físico transita entre estados periódicos estables y estados caóticos. Inherente a algunas formas de intermitencia es la memoria a largo plazo con un\(1/f\) espectro [44]. Esto se ha establecido para muchos sistemas físicos y biológicos.

Mapa Logístico

Un ejemplo clásico de intermitencia, y el primero ampliamente aceptado, es el siguiente modelo de dinámica poblacional. Si\(t_{n}\) denota tiempo discreto y (el número real)\(x_{n}\) denota la relación de la población existente con respecto a la población máxima posible en\(t_{n}\) (así\(x_{n}\) es entre\(0\) y\(1\)), entonces lo que se llama el mapa logístico proporciona la relación poblacional,\(x_{(n+1)}\), en el momento \(t_{n+1}\). El mapa logístico es [45]

\[\label{eq:12}F_{\lambda}(x)=\lambda x_{n}(1-x_{n}) \]

y así

\[\label{eq:13}x_{n+1}=F_{\lambda}(x) \]

Aquí\(\lambda\) hay un número positivo que representa la tasa combinada de reproducción e inanición. Por lo que determinan las condiciones ambientales\(\lambda\), lo que se constriñe para que\(0 <\lambda\leq 4\) Dependiendo de\(\lambda\), el mapa logístico (es decir, Ecuación\(\eqref{eq:12}\)) producirá una población estable o una población aleatoria dependiendo del valor de\(\lambda\), con la\(\lambda = 4\) producción de ruido blanco.

El ruido térmico produce fluctuaciones aleatorias en la amplitud y fase de una señal sinusoidal que se está procesando en un sistema electrónico no lineal como un amplificador o un oscilador. Denotando las fluctuaciones de amplitud térmica por\(a_{t,I} (t)\) y las fluctuaciones de fase térmica por\(\phi_{t,I} (t)\), una señal sinusoidal con amplitud media\(A\) y una fase inicial de cero es

\[\label{eq:14}x(t)=A[1+a_{t,I}(t)]\cos[\omega t+\phi_{t,I}(t)] \]

Utilizando el mapa logístico con\(\lambda = 4\) (que produce ruido blanco) para determinar\(a_{t,I} (t)\) y\(\phi_{t,I} (t)\), una señal sinusoidal con ruido térmico (blanco) es como se muestra en la Figura\(\PageIndex{9}\). Usando\(a_{t,I} (t)\) y\(\phi_{t,I} (t)\) determinado a partir de una distribución gaussiana produciría el mismo resultado cualitativo. Por supuesto, la mayor parte de este ruido sería fácil de eliminar mediante el filtrado de paso de banda, pero el ruido térmico seguirá apareciendo dentro del ancho de banda finito de la señal. Simplemente es más fácil visualizar el efecto del ruido trazándolo en esta escala.

\(\eqref{eq:12}\)La ecuación es una ecuación simple no lineal con retroalimentación retardada que se mezcla\(x\) a lo largo del tiempo. Lo que se llama la tasa de mezcla describe el grado de correlación con eventos pasados y puede considerarse como una tasa de decaimiento exponencial. Sin embargo, con el mapa logístico,\(F_{\lambda} (x)\) en Ecuación\(\eqref{eq:12}\), la tasa de esta mezcla no es controlable.

Mapa logarítmico

Hay muchos mapas que conducirán a\(1/(\Delta f)\) efectos y uno de los más convenientes de usar en el modelado del ruido de parpadeo en la electrónica se llama el loga-

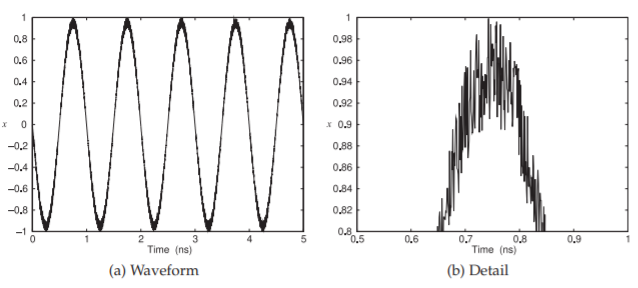
Figura\(\PageIndex{9}\): Señal sinusoidal con ruido blanco superpuesto calculada utilizando el mapa logístico en lugar de calcular el ruido como un proceso gaussiano.

mapa rítmico [46, 47]:

\[\label{eq:15}F_{\beta}(x)=\left\{\begin{array}{lll}{x(1+Y(\beta )x|\log(x)|^{1+\beta})}&{\text{if}}&{0\leq x\leq 1/2} \\ {2x-1}&{\text{if}}&{1/2<x\leq 1}\end{array}\right. \]

y así

\[\label{eq:16}x_{n+1}=F_{\beta}(x) \]

\(F_{\beta}(x)\)se define en el intervalo\(0 < x\leq 1\) y\(Y (\beta ) = 2(\log 2)^{−(1+\beta )}\) se elige para asegurar que\(\lim_{x→1/2}− f_{\beta}(x)=1\). (Tenga en cuenta que el mapa es discontinuo en\(x = 1/2\).) Si\(\Delta t\) es un intervalo de tiempo fijo, entonces\(x(t + \Delta t) = F_{\beta}(x(t))\).

El mapa logarítmico utiliza sólo un único parámetro,\(\beta\), que controla la velocidad de mezcla y, por lo tanto, la propiedad de memoria a largo plazo. La solución del mapa logarítmico, Ecuación\(\eqref{eq:15}\), con\(\beta = 0.000005\) se muestra en la Figura\(\PageIndex{10}\).

La transformada de Fourier de la secuencia trazada en la Figura\(\PageIndex{10}\) se muestra en la Figura\(\PageIndex{11}\) y su autocorrelación se muestra en la Figura\(\PageIndex{12}\). El espectro en la Figura\(\PageIndex{11}\) (anterior\(1\text{ Hz}\)) tiene una\(f^{−0.5}\) dependencia, y como la secuencia corresponde a voltaje, al cuadrar esto produce una característica\(1/f\) de potencia. La gráfica de autocorrelación en la Figura\(\PageIndex{12}\) muestra el lento decaimiento a largo plazo en la correlación con respecto al intervalo discreto,\(i\), entre los puntos de secuencia. Es decir, el mapa logarítmico describe un proceso con correlaciones que se descomponen lentamente. La correlación extendida es una medida de la velocidad de mezcla. Esta interpretación corresponde muy bien a la comprensión de los sistemas físicos, y en particular a los sistemas electrónicos. Se puede demostrar [47] que la tasa de decaimiento de correlación de este mapa está delimitada como

\[\label{eq:17} R(n)\leq B(\log n)^{-\beta} \]

donde\(n\) es el intervalo de tiempo\(n\) th. Así, se dice que el mapa describe una velocidad de mezcla logarítmica que se puede hacer tan lenta como se desee variando el valor de\(\beta\). Es esta dependencia de largo alcance la que produce\(f^{−1}\) (y\(f^{−2}\)\(f^{−3}\),, etc.) ruido. En un oscilador estos dan como resultado ruido de fase con\(1/(\Delta f)\)\(1/(\Delta f)^{2}\),\(1/(\Delta f)^{3}\),, etc. características. En los semiconductores, por ejemplo, el

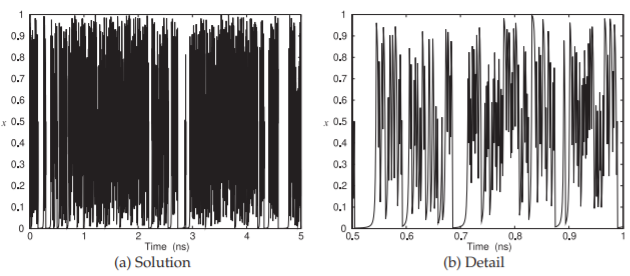
Figura\(\PageIndex{10}\): Solución del mapa logarítmico de Ecuación\(\eqref{eq:15}\) con (una semilla inicial aleatoria)\(x_{0} = 0.477347,\:\beta = 0.000005\), y\(t_{n+1} − t_{n} = 1\text{ ps}\).

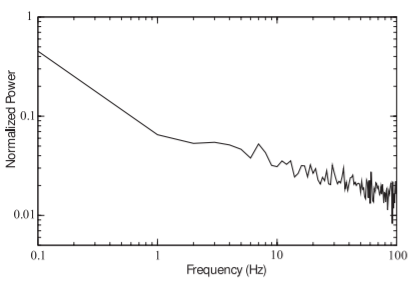
Figura\(\PageIndex{11}\): Espectro del mapa logarítmico con\(\beta = 0.000005\).

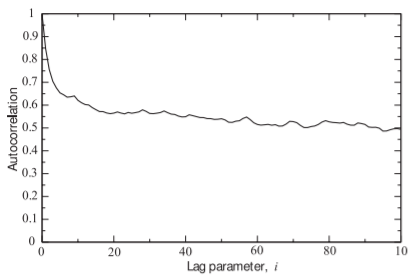
Figura\(\PageIndex{12}\): Gráfica de correlación del mapa logarítmico con\(\beta = 0.000005\) para una secuencia de millones de puntos.

la velocidad de mezcla está influenciada por la densidad de trampas [48] y la dispersión de celosía [49] con cuanto menor es la densidad de trampas (es decir, material semiconductor de mejor calidad) y cuanto menor es la cantidad de dispersión, menor es la tasa de mezcla y por lo tanto menor es el nivel de ruido de parpadeo. La retroalimentación retardada en el modelo de mapa caótico es consistente con la captura y la observación de que la reducción de trampas mejora el rendimiento del ruido de fase.

La mezcla de largo alcance indicada por el decaimiento lento de la función de correlación (ver Figura\(\PageIndex{12}\)) es clave para la\(f^{−1}\) respuesta. Otra función que produce una correlación a largo plazo es el proceso de Ornstein—Uhlenbeck [50, 51, 52] desarrollado para describir el movimiento browniano. La función de autocorrelación de este proceso decae exponencialmente y predice\(f^{−2}\) ruido pero no\(f^{−1}\) ruido [52]. El proceso de Ornstein—Uhlenbeck decae demasiado rápido para predecir la\(f^{−1}\) respuesta. Esto se discute más a fondo en [52].

Por lo que la solución de la Ecuación\(\eqref{eq:16}\) (el mapa logarítmico)\(\PageIndex{10}\), mostrada en la Figura, tiene dinámicas complicadas con largos periodos de estabilidad con transiciones rápidas entre niveles estables y rápidamente variables. La secuencia de\(x_{n}\) s depende de la condición de inicio (i.e.,\(x_{0}\)), pero no importa cómo comience, el espectro de potencia de la solución tiene una dependencia inversa de la frecuencia (es decir, es exactamente\(f^{−1}\)). El mapa logarítmico, como ocurre con todos los mapas caóticos, describe un proceso no lineal con retroalimentación retardada. Esto coincide con la situación en los sistemas físico, biológico, químico y financiero. Dado que casi todos los procesos físicos pueden describirse como un proceso no lineal (quizás débil) con retroalimentación retardada, la observación generalizada de\(1/f\) las fluctuaciones no es sorprendente. Entonces la base del\(1/f\) ruido es la más básica de los procesos físicos.

La intermitencia (descrita por mapas caóticos) da como resultado fluctuaciones aleatorias en la amplitud y fase de una señal sinusoidal procesada por un sistema electrónico no lineal como un amplificador u oscilador. Denotando la intermitencia de amplitud por\(a_{I}(t)\) y la intermitencia de fase por\(\phi_{I}(t)\), una señal sinusoidal con amplitud media\(A\) y una fase inicial de cero es

\[\label{eq:18}x(t)=A[1+a_{I}(t)]\cos[\omega t+\phi_{I}(t)] \]

Esta señal se muestra en la Figura\(\PageIndex{13}\) con las fluctuaciones de intermitencia logarítmica\(a_{I}(t)\) y\(\phi_{I}(t)\) como se muestra en la Figura\(\PageIndex{10}\), se calcula utilizando diferentes semillas. El efecto de las fluctuaciones de intermitencia es muy exagerado aquí para fines de visualización. En la práctica, las fluctuaciones a la escala mostrada en la Figura\(\PageIndex{13}\) podrían eliminarse usando un filtro de paso de banda. Sin embargo, las fluctuaciones son autosimilares (otra propiedad de los procesos caóticos) y se repiten a todas las escalas. En un sistema electrónico de paso de banda, las fluctuaciones de amplitud dentro de banda se suprimen por la no linealidad del dispositivo, pero las fluctuaciones de fase aparecen como ruido de fase en un oscilador.

5.8.6 Resumen

Se presentaron tres modelos de ruido de fase de oscilador. El modelo Leeson se basa en la conversión ascendente de ruido blanco de banda base produciendo ruido alrededor de la portadora del oscilador con una\(f^{−2}\) dependencia. El modelo Hajimiri y Lee se basa en un modelo lineal variable en el tiempo del oscilador con\(f^{-1}\) ruido en la banda base dando como resultado ruido de fase del oscilador con una\(1/(\Delta f)^{3}\) dependencia, y ruido blanco en la banda base y armónicos dando como resultado ruido alrededor de la frecuencia oscilante con un\(1/(\Delta f)^{2}\) dependencia. La conversión ascendente del ruido se ha demostrado como un mecanismo que describe

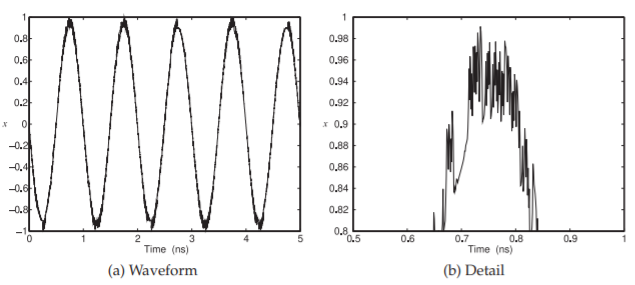
Figura\(\PageIndex{13}\): Señal sinusoidal con ruido de intermitencia superpuesto. Usando Ecuación\(\eqref{eq:18}\) con\(A = 0.9, a_{I} (t)\) escalado al intervalo\([0, 0.09]\),\(a_{I} (0) = 0.477347\) (antes de escalar),\(\phi_{I} (t)\) escalado a los\([0, 5]\) radianes del intervalo, y\(\phi_{I} (0) = 0.00915926\) (antes de escalar).

parte del ruido del oscilador observado. Ni el Leeson ni los modelos lineales variables en el tiempo describen el conjunto completo de observaciones de ruido de fase con\(1/(\Delta f)^{5},\ldots 1/(\Delta f)\) dependencias.

El modelo de mapa caótico es físicamente atractivo y describe el origen del ruido parpadeo como la retroalimentación retardada en el tiempo de la salida de un proceso no lineal. Esto puede producir una respuesta caótica llamada intermitencia que encarna la memoria a largo plazo. Se ha demostrado a través de la simulación que este modelo predice\(1/(\Delta f)^{0}\) las dependencias\(1/(\Delta f)^{3},\: 1/(\Delta f)^{2},\: 1/(\Delta f)^{1},\) y del ruido de fase. También es consistente con la caminata aleatoria vista en observaciones de dominio de tiempo del ruido del oscilador. Sin embargo, el caótico modelo basado en mapas aún no ha llevado a una fórmula compacta para el ruido de fase similar a la fórmula de Leeson. El desarrollo de un modelo compacto de ruido de fase (por ejemplo, como el modelo de Leeson) no será simple, ya que el cálculo entero y los análisis basados en la función de transferencia no se pueden usar directamente con un mapa caótico. Sin embargo, es claro que la descripción del ruido de fase se está acercando a una explicación física satisfactoria.

El ruido de fase también puede ser inducido por vibraciones [53, 54], y las señales espurias del entorno (como las acopladas de la red eléctrica) también pueden aparecer como ruido de fase.