5.12: Ejercicios

1. Dibuje el esquema de un circuito oscilador Hartley basado en un amplificador operacional.
2. Considera el circuito a continuación. Este es el circuito equivalente de un dispositivo activo con una conductancia negativa\(= 1/R_{D}\) conectado a un circuito de tanque que comprende condensador\(C_{T}\) e inductor\(L_{T}\), y luego una carga\(R_{L}\). La amplitud de oscilación se ajustará para que\(R_{D} = R_{L}\).

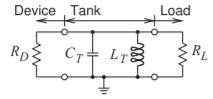
Figura\(\PageIndex{1}\)

1. Anote una fórmula para la frecuencia de oscilación\(f_{0}\).
2. ¿Qué es\(f_{0}\) si\(C_{T} = 1\text{ pF}\) y\(L_{T} = 1\text{ nH}\)?

3. El circuito de abajo es el circuito equivalente de un oscilador de reflexión con una conductancia negativa\(= 1/R_{D}\) conectada a un circuito tanque\(C_{T} = 0.1\text{ pF}\) y\(L_{T} = 0.5\text{ nH}\). ¿Cuál es la frecuencia de oscilación asumiendo que hay suficiente conductancia negativa para que ocurra la oscilación?

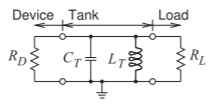
Figura\(\PageIndex{2}\)

4. El circuito de abajo es el circuito equivalente de un oscilador de reflexión con una conductancia negativa\(= 1/R_{D}\) conectado a un circuito tanque con una capacitancia\(C_{T} = 1\text{ pF}\) e inductancia\(L_{T} = 1\text{ nH}\). La carga consiste en un condensador\(C_{L}\) en paralelo con una resistencia\(R_{L}\). La amplitud de oscilación se ajustará para que\(R_{D} = R_{L}\).

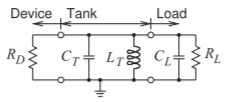
Figura\(\PageIndex{3}\)

1. Anote una fórmula simbólica para la frecuencia de oscilación\(f_{0}\).
2. ¿Qué es\(f_{0}\) si\(C_{L} = 0.2\text{ pF}\) y\(R_{L} = 50\:\Omega\)?

5. El circuito de abajo es el circuito equivalente de un oscilador de reflexión con una conductancia negativa\(= 1/R_{D}\) conectada a un circuito tanque\(C_{T} = 0.1\text{ pF}\) y\(L_{T} = 0.5\text{ nH}\). La capacitancia de la carga es\(C_{L} = 0.05\text{ pF}\) y la resistencia de carga es\(50\:\Omega\). ¿Cuál es la frecuencia de oscilación asumiendo que hay suficiente conductancia negativa para que ocurra la oscilación?

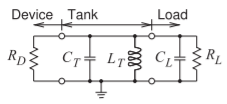
Figura\(\PageIndex{4}\)

6. El circuito de abajo es el circuito equivalente de un oscilador de reflexión con una conductancia negativa\(= 1/R_{D}\) conectado a un circuito tanque con una capacitancia\(C_{T} = 1\text{ pF}\) e inductancia\(L_{T} = 1\text{ nH}\). La carga consiste en un condensador\(C_{L} = 0.2\text{ pF}\) en paralelo con una resistencia\(R_{L} = 50\:\Omega\). Entre el circuito del tanque hay un\(3\text{ dB}\)\(50\:\Omega\) atenuador (es decir, el sistema está diseñado para la impedancia del sistema de\(50\:\Omega\)). La amplitud de oscilación se ajustará para que\(R_{D} = R_{L}\).

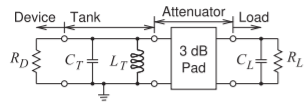
Figura\(\PageIndex{5}\)

1. Ignorar el condensador de carga\(C_{L}\), ¿cuál es la frecuencia de oscilación\(f_{0}\),, del oscilador?
2. A partir de ahora considere la capacitancia de carga. ¿Cuál es la frecuencia de oscilación sin el atenuador?
3. A la frecuencia calculada en (a), ¿cuál es la admitancia que busca en el atenuador desde el circuito del tanque con la carga que comprende\(C_{L}\) y\(R_{L}\)? [Pista usa el equivalente de red PI resistiva del atenuador.]
4. ¿Cuál es la resistencia de derivación equivalente y el circuito de condensador que buscan en el atenuador desde el oscilador? Esta es la carga efectiva vista por el dispositivo activo y el circuito del tanque.
5. ¿Cuál es la frecuencia de oscilación con el atenuador y la carga RC?
6. Usando sus resultados anteriores, discuta el efecto del atenuador en la reducción de la sensibilidad de oscilación en las condiciones de carga.

7. El circuito de abajo es el circuito equivalente de un oscilador de reflexión con una conductancia negativa\(= 1/R_{D}\) conectado a un circuito tanque con una capacitancia\(C_{T} = 1\text{ pF}\) e inductancia\(L_{T} = 1\text{ nH}\). La carga consiste en un condensador\(C_{L} = 0.2\text{ pF}\) en paralelo con una resistencia\(R_{L} = 50\:\Omega\). Entre el circuito del tanque hay un\(3\text{ dB }50\:\Omega\) atenuador (ti.e., el sistema está diseñado para la impedancia del sistema de\(50\:\Omega\)) y un filtro de paso de banda con una pérdida de inserción a la frecuencia de oscilación de\(2\text{ dB}\). La amplitud de oscilación se ajustará para que\(R_{D} = R_{L}\).

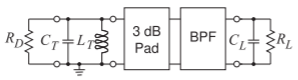
Figura\(\PageIndex{6}\)

1. Ignorar el condensador de carga\(C_{L}\), ¿cuál es la frecuencia de oscilación\(f_{0}\),, del oscilador?
2. A partir de ahora considere la capacitancia de carga. ¿Cuál es la frecuencia de oscilación sin el atenuador y el filtro de paso de banda?
3. A la frecuencia calculada en (a), ¿cuál es la admitancia que busca en el atenuador desde el circuito del tanque con el filtro paso banda y la carga que comprende\(C_{L}\) y\(R_{L}\)? [Pista: Considere que el efecto de la pérdida de inserción del filtro es una atenuación. Considere usar una red PI resistiva equivalente del atenuador más filtro de paso de banda.]
4. ¿Cuál es la resistencia de derivación equivalente y el circuito de condensador que buscan en el atenuador para el oscilador? Esta es la carga efectiva vista por el dispositivo activo y el circuito del tanque.
5. ¿Cuál es la frecuencia de oscilación con el atenuador y la carga RC?

8. A continuación se muestra un oscilador de reflexión junto con los\(\Gamma_{d}\) loci\(\Gamma_{r}\) y trazados en un gráfico de Smith. \(\Gamma_{r}\), el coeficiente de reflexión que mira hacia el resonador, gira en sentido horario a medida que aumenta la frecuencia. \(\Gamma_{d}\), el coeficiente de reflexión del dispositivo activo, depende de la amplitud pero es independiente de la frecuencia. La\(\Gamma_{d}\) curva con flecha traza los loci a\(\Gamma_{d}\) medida que aumenta la amplitud. [Pista: Considere la Figura 5.5.4.]

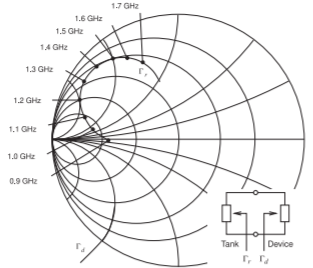
Figura\(\PageIndex{7}\)

1. En el\(\Gamma_{r}\) plano se muestra la región del Gráfico Smith identificando la oscilación.
2. En el\(\Gamma_{d}\) plano se muestra la región del Gráfico Smith identificando la oscilación.
3. ¿Cuál es la frecuencia de oscilación?

9. Considere un oscilador que puede modelarse como conexiones de derivación de una conductancia lineal,\(G_{r}\), una susceptancia lineal\(B_{r}\), una conductancia no lineal o de dispositivo\(G_{d}\), y una susceptancia no lineal o de dispositivo,\(B_{d}\).
   1. Dibuja el circuito.
   2. Usando\(G_{r},\: B_{r},\: G_{d},\) y\(B_{d}\), anote la condición del oscilador Kurokawa que establece una oscilación estable de frecuencia única.
   3. ¿Cuáles son las elecciones de diseño comunes\(G_{r},\: B_{r},\: G_{d},\) y\(B_{d}\) hechas que simplifican la condición del oscilador Kurokawa? Anote la condición de oscilación Kurokawa simplificada resultante.
10. Un oscilador tiene una conductancia lineal\(G_{r}\), una susceptancia lineal\(B_{r}\), una conductancia no lineal o de dispositivo\(G_{d}\), y una susceptancia no lineal o de dispositivo\(B_{d}\), todo en derivación. El coeficiente de reflexión que mira a la red lineal es\(\Gamma_{r}\) y el coeficiente de reflexión que mira al dispositivo es\(\Gamma_{d}\).
    1. Utilice un boceto de gráfico Smith para mostrar los loci de las admitancias lineales y no lineales (o equivalentemente sus coeficientes de reflexión\(\Gamma_{r}\) y\(\Gamma_{d}\)) para el caso en que la pérdida en la red lineal sea baja (i.e.\(G_{r}\approx 0\)). Haga esto cuando la señal oscilante sea pequeña y cuando haya alcanzado el estado estacionario. Indicar el punto de oscilación en estado estacionario. (Puede usar el negativo o el inverso de cualquiera\(\Gamma_{r}\) o\(\Gamma_{d}\) según corresponda.)
    2. Use un boceto de gráfico de Smith para mostrar los loci de las admitancias lineales y no lineales (o equivalentemente sus coeficientes de reflexión para el caso en que la pérdida en la red lineal sea alta (es decir,\(G_{r}\) no se puede ignorar). Haga esto cuando la señal oscilante sea pequeña y cuando haya alcanzado el estado estacionario. (Se puede utilizar el negativo de la inversa de cualquiera\(\Gamma_{r}\) o\(\Gamma_{d}\) según corresponda.)
11. El circuito equivalente de un oscilador se muestra a continuación con\(R_{L} = 50\:\Omega,\)\(C_{T} = 1\text{ pF}\) e inductancia\(L_{T} = 0.1\text{ nH}\).

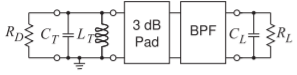
Figura\(\PageIndex{8}\)

1. ¿Cuál es la frecuencia de oscilación asumiendo que hay suficiente conductancia negativa para que ocurra la oscilación?
2. ¿Qué es\(R_{D}\) cuando hay oscilación?

12. A continuación se muestra un oscilador de reflexión junto con los\(\Gamma_{d}\) loci\(\Gamma_{r}\) y trazados en un gráfico de Smith. \(\Gamma_{r}\), el coeficiente de reflexión que mira hacia el resonador, gira en sentido horario a medida que aumenta la frecuencia. \(\Gamma_{d}\), el coeficiente de reflexión del dispositivo activo, depende de la amplitud pero es independiente de la frecuencia. La curva con flecha traza los loci de γD a medida que aumenta la amplitud. [Pista: Considere la Figura 5.5.4.]

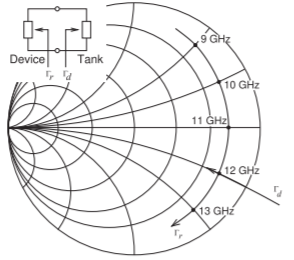
Figura\(\PageIndex{9}\)

1. En el\(\Gamma_{r}\) plano se muestra la región del Gráfico Smith identificando la oscilación.
2. En el\(\Gamma_{d}\) plano se muestra la región del Gráfico Smith identificando la oscilación.
3. ¿Cuál es la frecuencia de oscilación?

13. El estudio de caso presentado en la Sección 5.6 describió el diseño de un\(5\text{ GHz}\) VCO. La salida del oscilador fue seguida por un atenuador Pi resistivo y luego un filtro pasabanda. Cuál es la atenuación (en decibelios) y la impedancia del sistema del atenuador. [Pista: Deberá leer atentamente la Sección 5.6.]
14. Considere un emisor común BJT Clapp oscilador.
    1. Dibuje el esquema del oscilador sin el circuito de polarización.
    2. Redibuje el circuito oscilador incluyendo el circuito de polarización.
15. Considera un oscilador BJT Hartley.
    1. Dibuje el esquema del circuito oscilador en la configuración de base común. No mostrar el circuito de polarización.
    2. Redibuje el esquema del circuito oscilador en la configuración de base común, esta vez mostrando el circuito de polarización.
16. Considera un oscilador FET Clapp.
    1. Dibuje el esquema del circuito oscilador en la configuración de drenaje común. No mostrar el circuito de polarización.
    2. Redibuje el esquema del circuito oscilador, esta vez mostrando el circuito de polarización.
17. Considera un oscilador FET Hartley.
    1. Dibuje el esquema del circuito oscilador en la configuración de fuente común. No mostrar el circuito de polarización.
    2. Redibuje el esquema del circuito oscilador, esta vez mostrando el circuito de polarización.
18. Considere un oscilador FET Clapp de fuente común.
    1. Dibuja el esquema del oscilador sin sesgar.
    2. Redibuje el circuito del oscilador incluyendo las fuentes de corriente de polarización.
19. Derivar una expresión para la frecuencia de oscilación del oscilador Colpitts BJT en la configuración de emisor común mostrada en la Figura 5.8.1 (b).
20. Un oscilador de retroalimentación de dos puertos se muestra en la Figura 5.2.1.
    1. Dibuja el esquema de un oscilador Colpitts de retroalimentación.
    2. Considerando que el amplificador en el oscilador de retroalimentación tiene una ganancia que es independiente de la frecuencia, cuál es la frecuencia de oscilación si los componentes de la red de retroalimentación Colpitts son\(C_{1} = C_{2} = 2\text{ pF}\) y\(L_{3} = 5\text{ nH}\). Ignorar cualquier cambio de fase introducido por el amplificador.
21. Un oscilador de retroalimentación de dos puertos se muestra en la Figura 5.2.1.
    1. Dibuja el esquema de un oscilador Colpitts de retroalimentación.
    2. Considerando que el amplificador en el oscilador de retroalimentación tiene una ganancia que es independiente de la frecuencia, cuál es la frecuencia de oscilación si los componentes de la red de retroalimentación Colpitts son\(C_{1} = 1\text{ pF},\: C_{2} = 3\text{ pF}\), y\(L_{3} = 1\text{ nH}\). Ignorar cualquier cambio de fase introducido por el amplificador.
22. Un oscilador de retroalimentación de dos puertos se muestra en la Figura 5.2.1.
    1. Dibuja el esquema de un oscilador Colpitts de retroalimentación.
    2. Considerando que el amplificador en el oscilador de retroalimentación tiene una ganancia que es independiente de la frecuencia, ¿cuál es la frecuencia de oscilación si los componentes de la red de retroalimentación Colpitts son\(C_{1} = 5\text{ pF},\: C_{2} = 1\text{ pF}\), y\(L_{3} = 10\text{ nH}\)? Ignorar cualquier cambio de fase introducido por el amplificador.
23. Un VCO FET diferencial negativo-gm, como se muestra en la Figura 5.7.1, tiene\(C = 0.2\text{ pF}\) y\(L = 0.2\text{ nH}\). \(V_{DD} = 5\text{ V}\)y el circuito está polarizado para que para cada transistor\(g_{m} = 1\text{ mS}\). La salida en el colector del transistor acciona una\(1\text{ k}\Omega\) carga. Ignorar los parásitos internos del transistor y se debe considerar la posibilidad de que el circuito no oscile. ¿Cuál es la frecuencia de oscilación del oscilador?
24. Un VCO FET diferencial negativo-gm, como se muestra en la Figura 5.7.1, tiene\(C = 0.2\text{ pF}\) y\(L = 0.2\text{ nH}\). \(V_{DD} = 5\text{ V}\)y el circuito está polarizado para que para cada transistor\(g_{m} = 1\text{ mS}\). La salida en el colector del transistor acciona una carga\(50\:\Omega\) diferencial que está en paralelo con un\(0.5\text{ pF}\) condensador. Ignorar los parásitos internos del transistor y se debe considerar la posibilidad de que el circuito no oscile.
    1. Dibuja el esquema del oscilador con la carga.
    2. Dibuja el circuito de tanque equivalente del oscilador. Esto deberá incluir el efecto de la carga.
    3. ¿Cuál es la frecuencia de oscilación del oscilador?
25. Un VCO FET diferencial negativo-gm, como se muestra en la Figura 5.7.1, tiene\(C = 0.2\text{ pF}\) y\(L = 0.2\text{ nH}\). \(V_{DD} = 5\text{ V}\)y el circuito está polarizado para que para cada transistor\(g_{m} = 1\text{ mS}\). La salida en el colector del transistor acciona una carga\(50\:\Omega\) diferencial que está en paralelo con un\(1\text{ pF}\) condensador. Ignorar los parásitos internos del transistor y se debe considerar la posibilidad de que el circuito no oscile. ¿Cuál es la frecuencia de oscilación del oscilador?
26. Un oscilador Colpitts emisor común, como se muestra en la Figura 5.8.1 (a), tiene\(C_{1} = 1\text{ pF}\),\(C_{2} = 2\text{ pF}\), y\(L_{3} = 2\text{ nH}\). \(L_{C}\)es un inductor de estrangulador. \(V_{CC} = 5\text{ V}\)y el circuito está polarizado para que\(g_{m} = 1\text{ mS}\). Ignorar los parásitos internos del transistor. ¿Cuál es la frecuencia de oscilación del oscilador? [Ejemplo de Parallels 5.7.1]
27. Un oscilador Colpitts emisor común, como se muestra en la Figura 5.8.1 (a), tiene\(C_{1} = 0.1\text{ pF}\),\(C_{2} = 0.2\text{ pF}\), y\(L_{3} = 0.5\text{ nH}\). \(L_{C}\)es un inductor de estrangulador. \(V_{CC} = 5\text{ V}\)y el circuito está polarizado para que\(g_{m} = 1\text{ mS}\). Ignorar los parásitos internos del transistor. ¿Cuál es la frecuencia de oscilación del oscilador? [Ejemplo de Parallels 5.7.1]
28. Un sistema de comunicación digital tiene una tasa de símbolos de\(1\text{ MS/s}\).
    1. ¿Cuál es el ruido de fase de frecuencia más alto que afectará la tasa de error de bits del sistema de comunicación? (Podría ser\(1\text{ MHz}\),\(2\text{ MHZ}\), sin límite\(0.5\text{ MHz}\),, etc.)
    2. ¿Qué cambios haría en el sistema (por ejemplo, componentes añadidos como un atenuador, filtro, amplificador, etc.) que reducirán el impacto del ruido de fase de alto desplazamiento?
29. Un sistema de comunicación QPSK tiene una velocidad de bits transmitida de\(100\text{ kbit/s}\). Considera que el esquema de modulación QPSK es ideal.
    1. ¿Cuál es la tasa de símbolos?
    2. ¿Qué le haría al sistema (por ejemplo, componentes agregados) para reducir el impacto del ruido de fase de alto desplazamiento?
30. Un sistema de comunicación QPSK tiene una velocidad de bits transmitida de\(1\text{ Mbit/s}\). El esquema de modulación QPSK es ideal (\(2\text{ bit/s/Hz}\). El procesamiento DSP es tal que el ruido de fase más lento que la duración de los\(5\) símbolos no tiene ningún efecto en el rendimiento del sistema de comunicación.
    1. ¿Cuál es la tasa de símbolos?
    2. ¿Cuál es el ruido de fase de menor frecuencia que afectará al sistema de comunicación?
31. Un oscilador tiene ruido de fase que se reduce lejos de la frecuencia central de oscilación,\(f_{\text{osc}}\) a la velocidad de\(1/\Delta f^{2}\) donde\(\Delta f\) es el desplazamiento de frecuencia\(f_{\text{osc}}\). Si el ruido de fase en el desplazamiento de\(100\text{ MHz}\) frecuencia de la frecuencia de oscilación es\(−100\text{ dBc/Hz}\), ¿en qué se encuentra el ruido de fase\(10\text{ MHz}\)?
32. El ruido de fase de un oscilador medido en\(1\text{ MHz}\) es\(−136\text{ dBc/Hz}\). Si el ruido de fase varía como\(1/(\Delta f)\), ¿dónde\(\Delta f\) está el desplazamiento de la frecuencia central de oscilación, cuál es el ruido de fase en el\(100\text{ kHz}\) desplazamiento?
33. Un oscilador de microondas de fase bloqueada normalmente utiliza un\(Q\) oscilador bajo. Para tal oscilador el ruido de fase a la frecuencia que afecta a los sistemas de microondas tiene una relación cuadrada inversa con la frecuencia. El ruido de fase medido en\(100\text{ kHz}\) es\(−106\text{ dBc/Hz}\), ¿a qué se refiere el ruido de fase\(1\text{ MHz}\)?
34. Un oscilador de microondas de fase bloqueada normalmente utiliza un\(Q\) oscilador bajo. Para tal oscilador el ruido de fase a la frecuencia que afecta a los sistemas de microondas a menudo tiene una relación cuadrada inversa con la frecuencia. El ruido de fase medido en\(1\text{ MHz}\) es\(−125\text{ dBc/Hz}\), ¿en qué se encuentra el ruido de fase\(100\text{ kHz}\)?

5.12.1 Ejercicios por Sección

\(†\)desafiante,\(‡\) muy desafiante

\(§5.2\: 1\)

\(§5.3\: 2†, 3†, 4†, 5†, 6‡, 7‡, 8, 9, 10, 11\)

\(§5.5\: 12\)

\(§5.6\: 13†\)

\(§5.7\: 14†, 15†, 16†, 17†, 18†, 19†, 20†, 21†, 22†, 23†, 24†, 25†, 26†, 27†\)

\(§5.8\: 28†, 29†, 30†, 31, 32†, 33†, 34†\)

5.12.2 Respuestas a ejercicios seleccionados

4. \(4.594\text{ GHz}\)

6. d)\(49.8\:\Omega,\: 99.6\text{ fF}\)
7. e)\(4.883\text{ MHz}\)

13. \(49.8\:\Omega,\: 2.97\text{ dB}\)

19. \(\sqrt{\frac{C_{1}+C_{2}}{L_{3}C_{1}C_{2}}}\)
20. \(1.592\text{ GHz}\)

23. \(25.16\text{ GHz}\)
24. c)\(10.27\text{ GHz}\)

30. \(100\text{ GHz}\)

34. \(-105\text{ dBc/Hz}\)