1.1: Componentes básicos en una CPU

Última actualización
Guardar como PDF

Page ID: 80679

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Esta sección cubre los componentes básicos en una CPU. Cubre las puertas que se utilizan en la CPU, y cuatro CI comunes utilizados en una CPU, el sumador, el decodificador, el multiplexor y el registro.

1.1.1 Operaciones booleanas

Las puertas son implementaciones de hardware de operaciones booleanas. Las operaciones booleanas son operaciones que toman uno o más valores binarios y calculan un resultado. Por ejemplo, la operación AND toma 2 valores binarios (con 0 = false y 1 = true) y calcula una salida binaria. Para las operaciones AND, las entradas de 0 Y 0, 0 Y 1, y 1 Y 0 todas dan 0 (false), y la entrada de 1 Y 1 rinde 1 (true). Esto normalmente se implementa usando una tabla de verdad, de la siguiente manera:

Tabla 1-1: Mesa de verdad para puerta Y
Entrada		Salida
A	B	Y
0	0	0
0	1	0
1	0	0
1	1	1

En este texto se utilizarán 5 operadores booleanos, los AND, OR, NOT, XOR y NAND. El NOT es una función unaria (solo toma una entrada), y así se da en la Tabla 1-2.

Tabla 1-2: Mesa de verdad para puerta NOT
Entrada	Salida
A	NO
0	1
1	0

Los operadores AND, OR, XOR y NAND son binarios (tomando dos entradas) y se muestran en la Tabla 1- 3 a continuación.

Tabla 1-3: Tabla de verdad para puertas AND, OR, XOR y NAND
Entrada		Salida
A	B	Y	O	XOR	NAND
0	0	0	0	0	1
0	1	0	1	1	1
1	0	0	1	1	1
1	1	1	1	0	0

1.1.2 Circuitos integrados

Un circuito integrado (IC) es una colección de puertas que se utilizan para construir componentes para implementar un comportamiento. Los componentes de un CI son puertas simples, y todos los CI en este capítulo se pueden reducir fácilmente a puertas AND, OR, NOT, XOR y NAND. Así como las puertas transforman mecánicamente la entrada en salida, los CI también hacen una transformación mecánica de entradas en salidas.

Los CI que se describirán en este capítulo son el Adder, Decoder, Multiplexor y Flip Flop.

1.1.3 ALU (Adder)

La Unidad Lógica Aritmética (ALU) es el componente central de la CPU. Realiza todas las operaciones aritméticas y lógicas sobre los datos. Todo lo demás en la CPU está diseñado para proporcionar datos para que la ALU opere.

El ALU es normalmente una caja negra que proporciona las operaciones para la CPU en dos operandos. Esta caja negra es responsable de todas las operaciones que realiza la CPU, incluyendo no solo operaciones enteras y lógicas, sino también cálculos de punto flotante. Las operaciones como los cálculos de punto flotante son muy complejas, y a menudo se implementan en coprocesadores. Para mantener las cosas simples, los únicos tipos de datos permitidos para la CPU en este texto serán enteros, y solo se permitirán operaciones enteras y lógicas.

Una visión general de una ALU se puede ver en la ALU típica que se muestra a continuación. Una ALU toma dos argumentos, e implementa y opera, como sumar, restar, multiplicar y dividir operaciones en estos dos operandos. La ALU también permite operaciones como operaciones booleanas (AND, OR, XOR, etc), desplazamiento de bits y comparación.

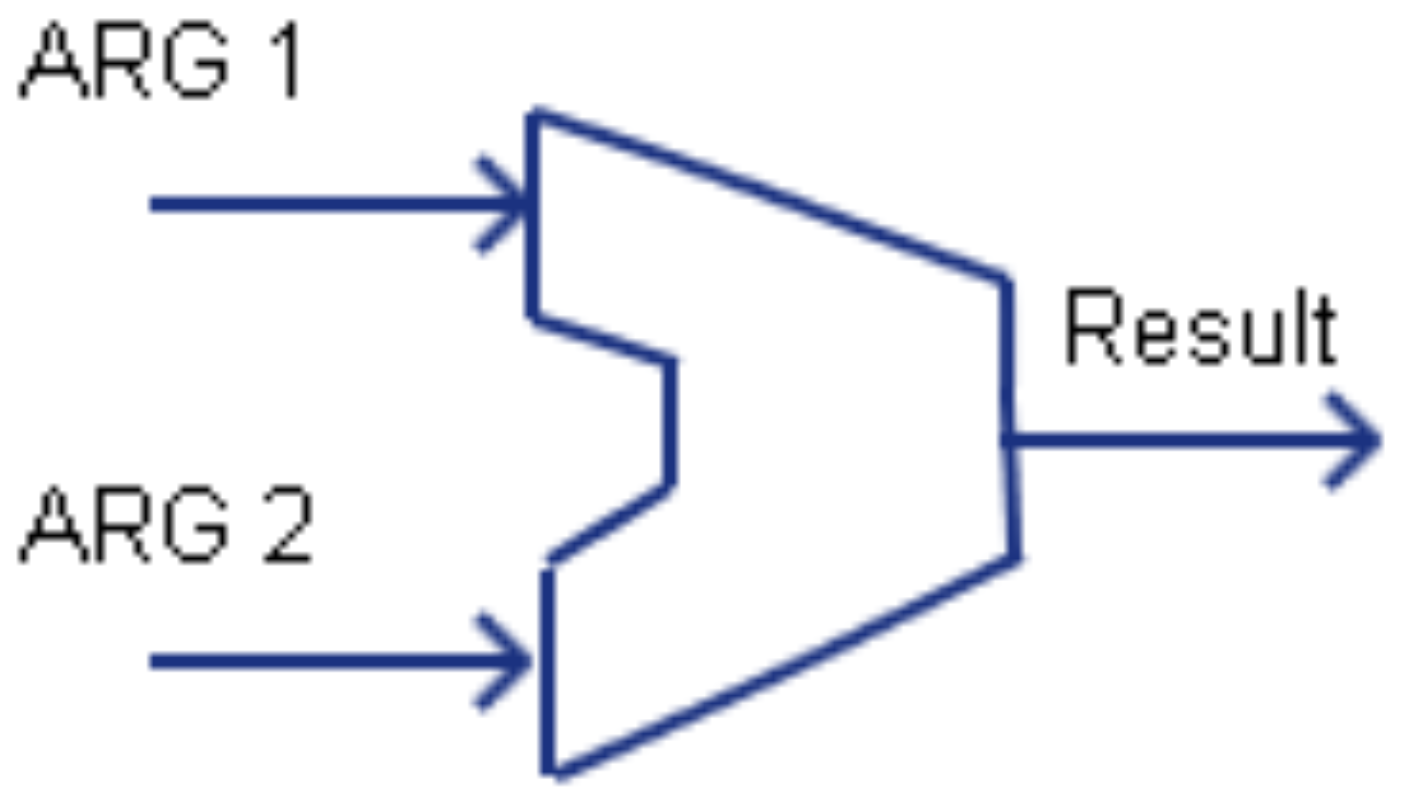
Screen Shot 2020-07-02 en 4.49.42 PM.png

Debido a que la única operación de ALU cubierta en el texto recomendado en los CI es un sumador, la ALU utilizada en la implementación Logisim de la CPU contendrá solo un circuito sumador. Usando un sumador, se implementan tanto la suma como la resta. Una configuración más robusta para una ALU se puede encontrar en las notas adicionales a las que se puede acceder para este texto.

1.1.4 Decodificador

Un decodificador es un IC que divide un número de n bits en 2n líneas de salida separadas. Por ejemplo, considere un número de 2 bits, que puede tener 4 valores, 0x0... 0x3. Un decodificador tomaría como entrada 2 líneas de entrada que representan el número de 2 bits, y encendería una (y solo una) de las cuatro líneas de salida. La línea que está encendida corresponde al valor de la entrada de 2 bits. Entonces en el siguiente diagrama, si la entrada de 2 bits tiene ambas líneas altas (que representan “11”), y la línea de salida 3 está encendida.

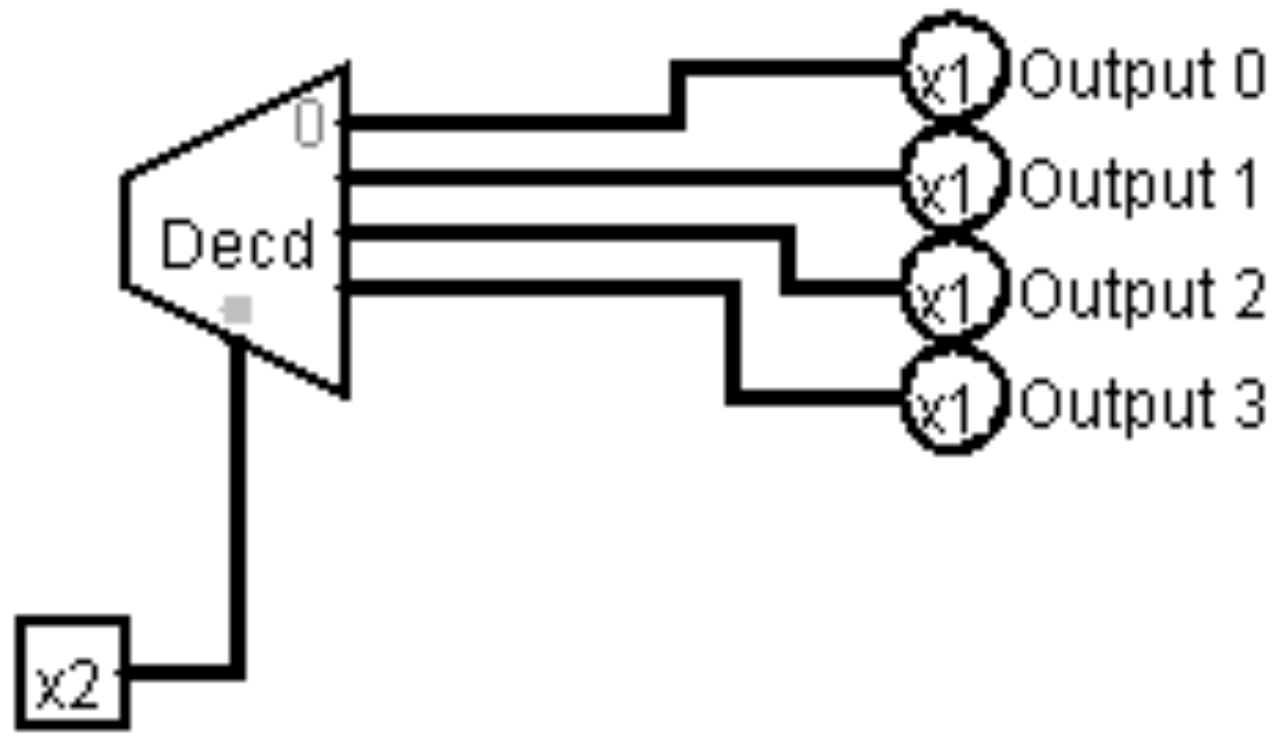
Screen Shot 2020-07-02 en 4.51.19 PM.png

1.1.5 Multiplexor

Un multiplexor es un IC que selecciona entre diferentes entradas. En el siguiente diagrama, los 8 bits utilizados por la Salida pueden provenir del Registro 1 o del Registro 2. El MUX selecciona qué valor de 8 bits usar. Si Seleccionar entrada es 0, se elige Registrar 1, y si Seleccionar entrada es 1, se elige Registrar 2.

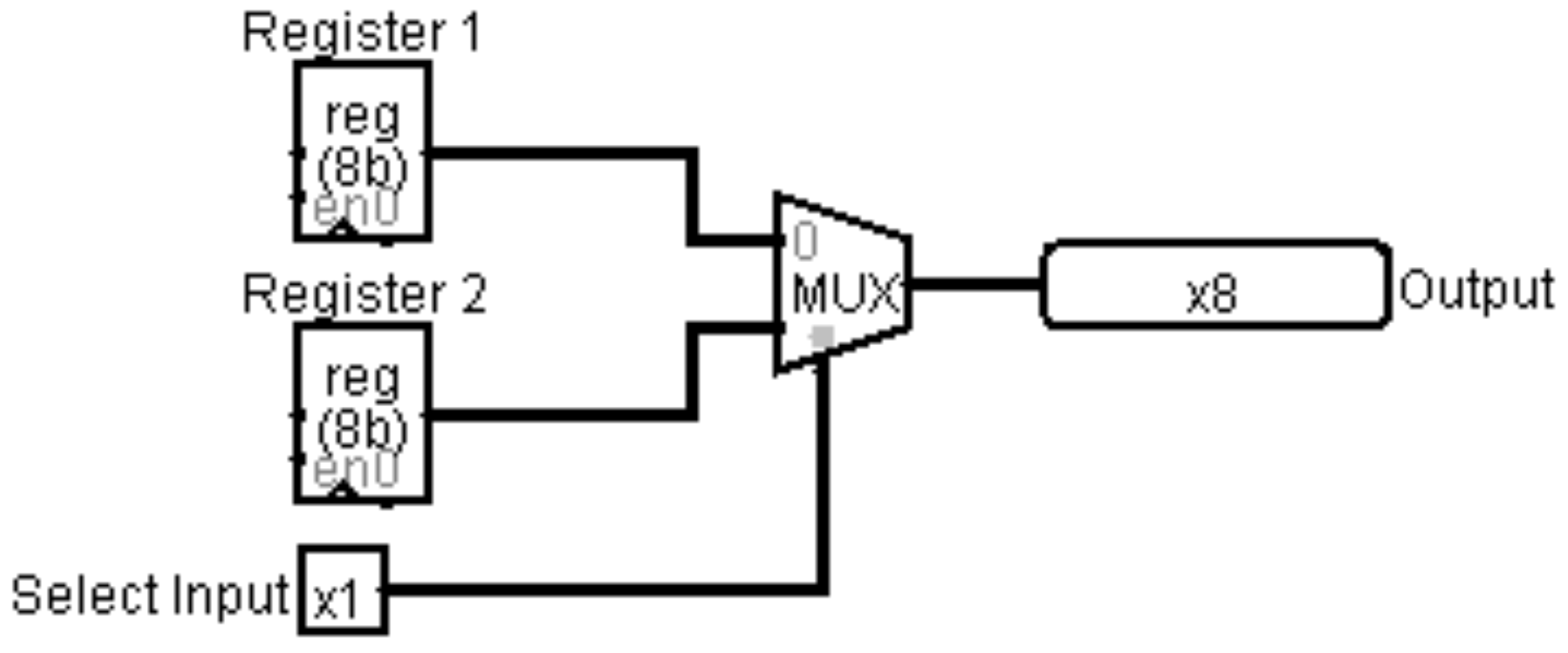
Screen Shot 2020-07-02 at 4.54.08 PM.png

1.1.6 Registros (Flip Flops D) y Memoria

La memoria es diferente a los otros CI en que es sincrónica, donde sincrónica significa que la celda de memoria tiene un valor que a intervalos de tiempo discretos. Un ejemplo de este comportamiento es el $ac en el siguiente fragmento de programa:

clac    <- time = t0, $ac = 5
addi 5  <- time = t1, $ac = 5
addi 7  <- time = t2, $ac = 5  
subi 2  <- time = t3, $ac = 5

Este programa muestra que el valor de la memoria, $ac, cambia discretamente con el tiempo. Este comportamiento discreto se logra mediante un reloj del sistema. Un reloj de sistema es un circuito oscilador electrónico que produce una onda cuadrada con una frecuencia precisa. A continuación se muestra una ilustración de una onda cuadrada.

Screen Shot 2020-07-02 at 4.58.38 PM.png

En una onda cuadrada, el valor es siempre 0 o 1, y la memoria utiliza la transición de 0 a 1 (el borde positivo) para cambiar el valor de todos los componentes de memoria. Así, las celdas de memoria tienen valores discretos que cambian en cada pulso de reloj.

Cualquier celda de memoria en una CPU normalmente se llama registro. La memoria de registro normalmente consiste en Static Ram (SRAM), y se implementa usando Flip Flops. La memoria principal de la computadora suele ser Dynamic Ram (DRAM)., sin embargo alguna memoria, particularmente la memoria caché, se puede implementar con SRAM. Los detalles de la memoria están más allá del alcance de este texto, y todo lo que el lector necesita saber es que la memoria de registro suele ser SRAM y se encuentra dentro de la CPU.