3.8.2: Transformación discreta de coseno
- Page ID
- 82085
En el lenguaje del álgebra lineal, la fórmula
\[\mathbb{Y} = \mathbb{C}\mathbb{X}\mathbb{D} \tag{3.10}\]
representa una transformación de la matriz\(\mathbb{X}\) en una matriz de coeficientes\(\mathbb{Y}\). Suponiendo que las matrices de transformación\(\mathbb{C}\) y\(\mathbb{D}\) tienen inversas\(\mathbb{C}^{−1}\) y\(\mathbb{D}^{−1}\) respectivamente, la matriz original puede ser reconstruida a partir de los coeficientes por la transformación inversa:
\[ \mathbb{X} = \mathbb{C}^{-1}\mathbb{Y}\mathbb{D}^{-1}. \tag{3.11}\]
Esta interpretación de\(\mathbb{Y}\) como coeficientes útiles para la reconstrucción de\(\mathbb{X}\) es especialmente útil para la Transformación del Coseno Discreto.
La Transformación Discreta de Coseno es una Transformación Lineal Discreta del tipo discutido anteriormente
\[\mathbb{Y} = \mathbb{C}^{T}\mathbb{X}\mathbb{C}\tag{3.12}\]
donde las matrices son todas de tamaño\(N×N\) y las dos matrices de transformación son transpuestas entre sí. La transformación se llama transformación de coseno porque la matriz\(\mathbb{C}\) se define como
\[\tag{3.13} {\mathbb{C}}_{m,n} = k_n \cos \begin{bmatrix} \dfrac{(2m + 1)n\pi}{2N} \end{bmatrix} \text{where } k_n = \begin{cases} \sqrt{1/N} & \mbox{if }n = 0 \\ \sqrt{2/N} & \mbox{if otherwise} \end{cases} \]
donde\(m, n = 0, 1, . . .(N − 1)\). Esta matriz\(\mathbb{C}\) tiene una inversa que es igual a su transposición:
\[\tag{3.14} \mathbb{C}^{-1} = \mathbb{C}.\]
Usando la Ecuación 3.12 con\(\mathbb{C}\) como se define en la Ecuación 3.13, podemos calcular el DCT\(\mathbb{Y}\) de cualquier matriz\(\mathbb{X}\), donde la matriz\(\mathbb{X}\) puede representar los píxeles de una imagen dada. En el contexto de la DCT, el procedimiento inverso descrito en la ecuación 3.11 se denomina Transformación de Coseno Discreta Inversa (IDCT):
\[\tag{3.15} \mathbb{X} = \mathbb{C}\mathbb{Y}\mathbb{C}^T.\]
Con esta ecuación, podemos calcular el conjunto de matrices base de la DCT, es decir: el conjunto de matrices al que cada uno de los elementos de\(\mathbb{Y}\) corresponde vía la DCT. Construyamos el conjunto de todas las imágenes posibles con un solo píxel distinto de cero cada una. Estas imágenes representarán los coeficientes individuales de la matriz\(\mathbb{Y}\). La Figura 3.7 (a) muestra el conjunto para imágenes de 4×4 píxeles. La Figura 3.7 (b) muestra el resultado de aplicar el IDCT a las imágenes de la Figura 3.7 (a). El conjunto de imágenes en la Figura 3.7 (b) se denominan base porque la DCT de cualquiera de ellas producirá una matriz\(\mathbb{Y}\) que tiene un único coeficiente distinto de cero, y así representan las imágenes base en las que la DCT “descompone” cualquier imagen de entrada.


Figura 3.7: (a) Imágenes de 4×4 píxeles que representan los coeficientes que aparecen en la matriz\(\mathbb{Y}\) a partir de la ecuación 3.15. Y, (b) correspondientes Transformaciones de Coseno Discreto Inversa, estos ICDTs pueden interpretarse como a las imágenes base que corresponden a los coeficientes de\(\mathbb{Y}\).
Recordando nuestra visión general de Transformaciones Lineales Discretas anterior, si queremos recuperar una imagen\(\mathbb{X}\) de su DCT simplemente\(\mathbb{Y}\) tomaríamos cada elemento de Y y lo multiplicaríamos por la matriz correspondiente de 3.7 (b). En efecto, la Figura 3.7 (b) introduce una propiedad muy notable de la base DCT: codifica la frecuencia espacial. La compresión se puede lograr ignorando aquellas frecuencias espaciales que tienen coeficientes DCT más pequeños. Piense en la imagen de un panel de ajedrez: tiene un componente de alta frecuencia espacial y se pueden eliminar casi todos los componentes de baja frecuencia. Por el contrario, las imágenes borrosas tienden a tener menos componentes de frecuencia espacial más altos, y luego los componentes de alta frecuencia, más abajo a la derecha en la Figura 3.7 (b), se pueden establecer en cero como una “aproximación aceptable”. Este es el principio para la compresión irreversible detrás de JPEG.
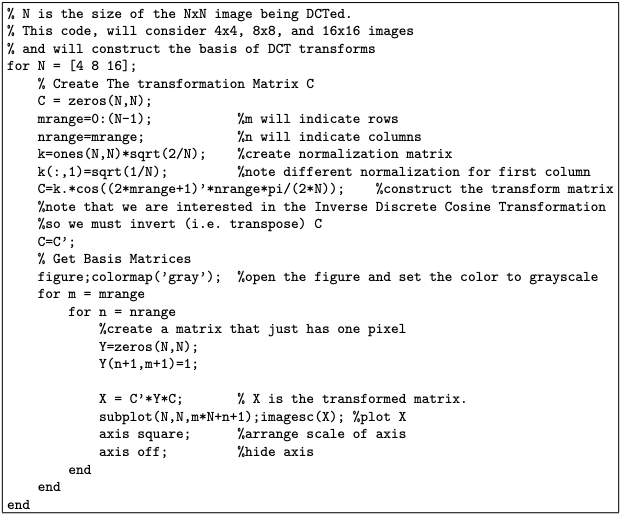
La Figura 3.8 muestra el código MATLAB para generar las imágenes de base como se muestra anteriormente para el DCT 4×4, 8×8 y 16x16.