7.1: Dinámica poblacional y demografía
- Page ID
- 82597
Introducción
Imagina navegar río abajo en una pequeña lancha motora una tarde de fin de semana; el agua es suave, y estás disfrutando del sol y la brisa fresca cuando de repente te golpea en la cabeza una carpa plateada de 20 libras. Este es un riesgo ahora en muchos ríos y sistemas de canales en Illinois y Missouri debido a la presencia de carpas asiáticas. Este pez, en realidad un grupo de especies que incluye el plateado, el negro, el pasto y el carpe de cabeza grande, ha sido cultivado y comido en China por más de mil años. Es uno de los recursos alimentarios acuícolas más importantes a nivel mundial. En Estados Unidos, sin embargo, la carpa asiática es considerada una especie invasora peligrosa que altera la estructura de la comunidad ecológica hasta el punto de amenazar a las especies nativas. Los efectos de especies invasoras (como la carpa asiática, la vid kudzu, el pez cabeza de serpiente depredador y el mejillón cebra) son solo un aspecto de lo que los ecologistas estudian para comprender cómo interactúan las poblaciones dentro de las comunidades ecológicas y qué impacto tienen las perturbaciones naturales e inducidas por el hombre en las características de comunidades.
Tamaño y Densidad de la Población
La población es un grupo de organismos de la misma especie que viven en la misma zona. El tamaño y la composición de una población fluctúan en respuesta a numerosos factores, incluyendo cambios estacionales y anuales en el ambiente, desastres naturales como incendios forestales y erupciones volcánicas, y competencia por recursos entre especies y dentro de ellas. El estudio estadístico de las poblaciones se llama demografía: un conjunto de herramientas matemáticas diseñadas para describir poblaciones e investigar cómo cambian. Muchas de estas herramientas fueron diseñadas para estudiar poblaciones humanas. Por ejemplo, las tablas de vida, que detallan la esperanza de vida de los individuos dentro de una población, fueron desarrolladas inicialmente por las compañías de seguros de vida para establecer tarifas de seguros. De hecho, si bien a veces se asume que el término “demografía” significa un estudio de poblaciones humanas, todas las poblaciones vivas pueden estudiarse utilizando este enfoque.
Las poblaciones se caracterizan por su tamaño poblacional (número total de individuos) y su densidad poblacional (número de individuos por unidad de área). Una población puede tener un gran número de individuos que se distribuyen densamente, o escasamente. También hay poblaciones con un pequeño número de individuos que pueden ser densos o muy escasamente distribuidos en un área local. El tamaño de la población puede afectar el potencial de adaptación porque afecta la cantidad de variación genética presente en la población. La densidad puede tener efectos en las interacciones dentro de una población como la competencia por la comida y la capacidad de los individuos para encontrar pareja. Los organismos más pequeños tienden a estar más densamente distribuidos que los organismos más grandes (Figura a continuación).
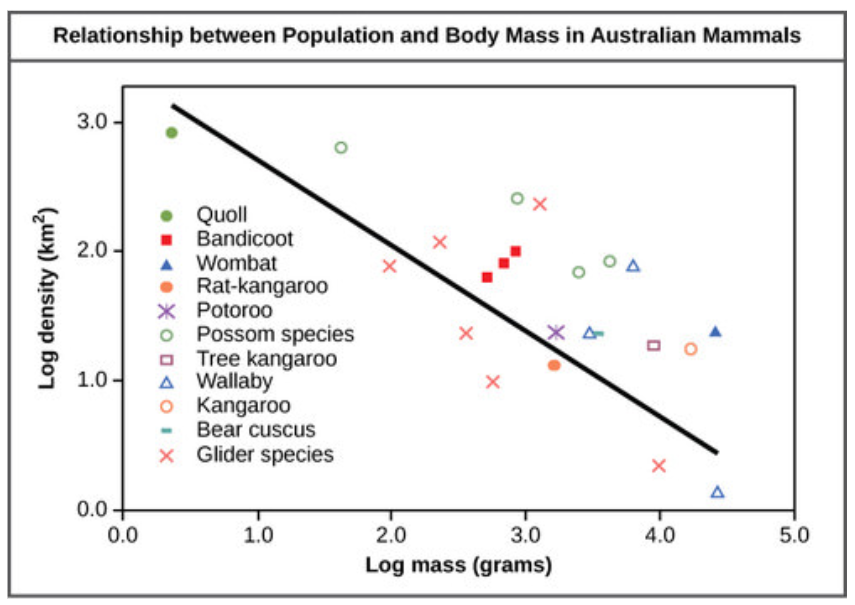
Estimación del tamaño de la población
La forma más precisa de determinar el tamaño de la población es contar todos los individuos dentro del área. Sin embargo, este método no suele ser logística ni económicamente factible, especialmente cuando se estudian grandes áreas. Por lo tanto, los científicos suelen estudiar poblaciones muestreando una porción representativa de cada hábitat y utilizan esta muestra para hacer inferencias sobre la población en su conjunto. Los métodos utilizados para muestrear poblaciones para determinar su tamaño y densidad se adaptan típicamente a las características del organismo que se estudia. Para organismos inmóviles como plantas, o para organismos muy pequeños y de movimiento lento, se puede usar un cuadrante. Un cuadrante es un cuadrado de madera, plástico o metal que se ubica aleatoriamente en el suelo y se usa para contar el número de individuos que se encuentran dentro de sus límites. Para obtener un conteo preciso utilizando este método, el cuadrado debe colocarse en ubicaciones aleatorias dentro del hábitat suficientes tiempos para producir una estimación precisa. Este método de conteo proporcionará una estimación tanto del tamaño de la población como de la densidad. El número y tamaño de las muestras de cuadratas depende del tipo de organismos y de la naturaleza de su distribución.
Para los organismos móviles más pequeños, como los mamíferos, a menudo se utiliza una técnica llamada marca y recaptura. Este método implica marcar una muestra de animales capturados de alguna manera y liberarlos de nuevo al ambiente para mezclarlos con el resto de la población; luego, se captura una nueva muestra y los científicos determinan cuántos de los animales marcados están en la nueva muestra. Este método supone que cuanto mayor sea la población, menor será el porcentaje de organismos marcados que serán recapturados ya que se habrán mezclado con más individuos sin marcar. Por ejemplo, si 80 ratones de campo son capturados, marcados y liberados en el bosque, entonces se captura un segundo atrapamiento de 100 ratones de campo y 20 de ellos son marcados, el tamaño de la población (N) se puede determinar usando la siguiente ecuación:
\[\dfrac{\text{number marked first catch}\times \text{total number second catch}}{\text{number marked second catch}} = N \nonumber \]
Usando nuestro ejemplo, el tamaño de la población sería de 400.
\[\dfrac{80\times 100}{20}=400 \nonumber \]
Estos resultados nos dan una estimación de 400 individuos totales en la población original. El número verdadero generalmente será un poco diferente de esto debido a errores de azar y posible sesgo causado por los métodos de muestreo.
Distribución de Especies
Además de medir la densidad, se puede obtener más información sobre una población observando la distribución de los individuos a lo largo de su área de distribución. Un patrón de distribución de especies es la distribución de individuos dentro de un hábitat en un momento determinado; se utilizan categorías amplias de patrones para describirlos.
Los individuos dentro de una población pueden distribuirse al azar, en grupos o equidistantes (más o menos). Estos se conocen como patrones de distribución aleatorios, agrupados y uniformes, respectivamente (Figura a continuación). Las diferentes distribuciones reflejan aspectos importantes de la biología de la especie; también afectan los métodos matemáticos requeridos para estimar el tamaño de la población. Un ejemplo de distribución aleatoria ocurre con el diente de león y otras plantas que tienen semillas dispersas por el viento que germinan dondequiera que caigan en ambientes favorables. Una distribución agrupada, se puede observar en plantas que dejan caer sus semillas directamente al suelo, como los robles; también se puede observar en animales que viven en grupos sociales (bancos de peces o manadas de elefantes). Se observa una distribución uniforme en plantas que secretan sustancias que inhiben el crecimiento de individuos cercanos (como la liberación de químicos tóxicos por las plantas de salvia). También se observa en especies animales territoriales, como los pingüinos que mantienen un territorio definido para la anidación. Los comportamientos defensivos territoriales de cada individuo crean un patrón regular de distribución de territorios de tamaño similar e individuos dentro de esos territorios. Así, la distribución de los individuos dentro de una población proporciona más información sobre cómo interactúan entre sí que una simple medición de densidad. Así como las especies de menor densidad podrían tener más dificultades para encontrar pareja, las especies solitarias con una distribución aleatoria podrían tener una dificultad similar en comparación con las especies sociales agrupadas en grupos.
Figura\(\PageIndex{2}\): Las especies pueden tener una distribución aleatoria, agrupada o uniforme. Las plantas como (a) los dientes de león con semillas dispersas por el viento tienden a distribuirse aleatoriamente. Los animales como (b) los elefantes que viajan en grupos exhiben una distribución agrupada. Las aves territoriales como (c) los pingüinos tienden a tener una distribución uniforme. (crédito a: modificación de obra de Rosendahl; crédito b: modificación de obra de Rebecca Wood; crédito c: modificación de obra de Ben Tubby)Demografía
Si bien el tamaño y la densidad de la población describen una población en un momento determinado, los científicos deben utilizar la demografía para estudiar la dinámica de una población. La demografía es el estudio estadístico de los cambios poblacionales a lo largo del tiempo: tasas de natalidad, tasas de mortalidad y expectativas de vida. Estas características poblacionales suelen mostrarse en una tabla de vida.
Las tablas de vida proporcionan información importante sobre la historia de vida de un organismo y la esperanza de vida de los individuos a cada edad. Se modelan a partir de tablas actuariales utilizadas por la industria aseguradora para estimar la esperanza de vida humana. Las tablas de vida pueden incluir la probabilidad de que cada grupo de edad muera antes de su próximo cumpleaños, el porcentaje de individuos sobrevivientes que mueren en un intervalo de edad determinado (su tasa de mortalidad y su esperanza de vida en cada intervalo. Un ejemplo de una tabla de vida se muestra en Tabla de un estudio de ovejas de montaña Dall, una especie nativa del noroeste de América del Norte. Observe que la población se divide en intervalos de edad (columna A). La tasa de mortalidad (por 1000) que se muestra en la columna D se basa en el número de individuos que mueren durante el intervalo de edad (columna B), dividido por el número de individuos que sobreviven al inicio del intervalo (Columna C) multiplicado por 1000.
\[\text {mortality rate} = \dfrac{\text{number of individuals dying}}{\text{number of individuals surviving}} \times 1000 \nonumber \]
Por ejemplo, entre los tres y cuatro años mueren 12 individuos de los 776 que quedaban de las 1000 ovejas originales. Este número se multiplica entonces por 1000 para dar la tasa de mortalidad por mil.
\[\text {mortality rate} = \dfrac{12}{776} \times 1000 \approx 15.5 \nonumber \]
Como se puede observar en los datos de la tasa de mortalidad (columna D), una alta tasa de mortalidad ocurrió cuando las ovejas tenían entre seis meses y un año de edad, y luego aumentó aún más de 8 a 12 años, después de lo cual hubo pocos sobrevivientes. Los datos indican que si una oveja de esta población sobreviviera hasta la edad de uno, podría esperarse que viviera otros 7.7 años en promedio, como lo muestran los números de esperanza de vida en la columna E.
|
A Intervalo de edad (años) |
B Número que muere en el intervalo de edad de 1000 nacidos |
C Número que sobrevive al inicio del intervalo de edad de 1000 nacidos |
D Tasa de mortalidad por 1000 vivos al inicio del intervalo de edad |
E Esperanza de vida o media de vida restante para quienes alcanzan el intervalo de edad |
|---|---|---|---|---|
| 54 | 1000 | 54.0 | 7.06 | |
| 145 | 946 | 153.3 | - | |
| 12 | 801 | 15.0 | 7.7 | |
| 13 | 789 | 16.5 | 6.8 | |
| 12 | 776 | 15.5 | 5.9 | |
| 30 | 764 | 39.3 | 5.0 | |
| 46 | 734 | 62.7 | 4.2 | |
| 48 | 688 | 69.8 | 3.4 | |
| 69 | 640 | 107.8 | 2.6 | |
| 132 | 571 | 231.2 | 1.9 | |
| 187 | 439 | 426.0 | 1.3 | |
| 156 | 252 | 619.0 | 0.9 | |
| 90 | 96 | 937.5 | 0.6 | |
| 3 | 6 | 500.0 | 1.2 | |
| 3 | 3 | 1000 | 0.7 |
Esta tabla de vida de Ovis dalli muestra el número de muertes, número de sobrevivientes, tasa de mortalidad y esperanza de vida en cada intervalo de edad para ovejas de montaña Dall.
Curvas de supervivencia
Otra herramienta utilizada por los ecologistas poblacionales es una curva de supervivencia, que es una gráfica del número de individuos que sobreviven en cada intervalo de edad versus tiempo. Estas curvas nos permiten comparar las historias de vida de diferentes poblaciones (Figura a continuación). Existen tres tipos de curvas de supervivencia. En una curva tipo I, la mortalidad es baja en los primeros y medianos años y ocurre principalmente en individuos mayores. Los organismos que presentan una supervivencia tipo I suelen producir pocas crías y proporcionan un buen cuidado a la descendencia aumentando la probabilidad de su supervivencia. Los humanos y la mayoría de los mamíferos presentan una curva de supervivencia tipo I. En las curvas de tipo II, la mortalidad es relativamente constante a lo largo de toda la vida, y es igualmente probable que la mortalidad ocurra en cualquier momento de la vida.
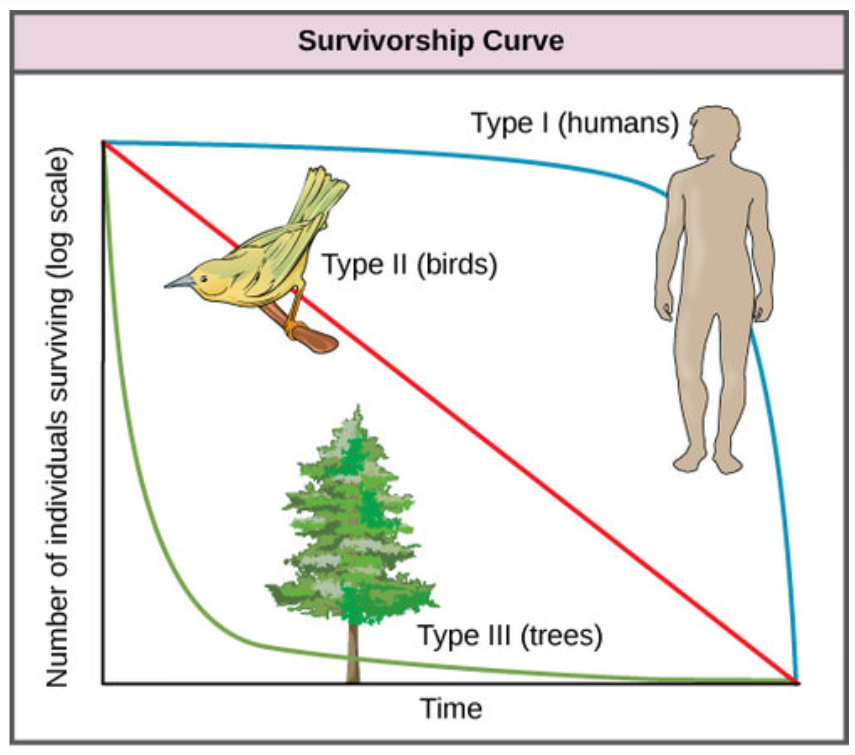
Muchas poblaciones de aves proporcionan ejemplos de una curva de supervivencia intermedia o tipo II. En las curvas de supervivencia tipo III, las edades tempranas experimentan la mayor mortalidad con tasas de mortalidad mucho menores para los organismos que llegan a años avanzados. Los organismos de tipo III suelen producir un gran número de crías, pero proporcionan muy poco o ningún cuidado para ellos. Los árboles e invertebrados marinos presentan una curva de supervivencia tipo III porque muy pocos de estos organismos sobreviven en su juventud, pero aquellos que llegan a la vejez tienen más probabilidades de sobrevivir por un período de tiempo relativamente largo.