3.8: Circuitos con Capacitores e Inductores

Última actualización
Guardar como PDF

Page ID: 85511

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Introduciendo cuando un circuito tiene condensadores e inductores distintos de resistencias y fuentes, se aplicará el concepto de impedancia.

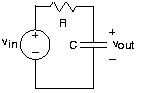
Consideremos un circuito que tenga algo más que resistencias y fuentes. Debido a KVL, sabemos que:

\[v_{in}=v_{R}+v_{out} \nonumber \]

La corriente a través del condensador viene dada por:

\[i=C\frac{\mathrm{d} v_{out}}{\mathrm{d} t} \nonumber \]

Esta corriente equivale a la que pasa a través de la resistencia. Sustituyendo:

\[v_{R}=Ri \nonumber \]

en la ecuación KVL y usando la relación v-i para el condensador, llegamos a

\[RC\frac{\mathrm{d} v_{out}}{\mathrm{d} t}+v_{out}=v_{in} \nonumber \]

La relación entrada-salida para circuitos que involucran elementos de almacenamiento de energía toma la forma de una ecuación diferencial ordinaria, que debemos resolver para determinar cuál es la tensión de salida para una entrada dada. A diferencia de los circuitos resistivos, donde obtenemos una relación explícita entrada-salida, ahora tenemos una relación implícita que requiere más trabajo para obtener respuestas.

En este punto, podríamos aprender a resolver ecuaciones diferenciales. Observe primero que incluso encontrar la ecuación diferencial que relaciona una variable de salida con una fuente suele ser muy tedioso. Las reglas de combinación en paralelo y en serie que se aplican a las resistencias no se aplican directamente cuando se producen condensadores e inductores. Tendríamos que atravesar las ecuaciones del circuito, simplificándolas hasta que finalmente encontráramos la ecuación que relacionaba la (s) fuente (s) con la salida. A principios del siglo XX, se descubrió un método que no sólo facilitaba la búsqueda de la ecuación diferencial, sino que simplificaba el proceso de solución en la situación más común. Aunque no fue original con él, Charles Steinmetz presentó el artículo clave que describe el enfoque de impedancia en 1893. Permite que los circuitos que contienen capacitores e inductores se resuelvan con los mismos métodos que hemos aprendido para resolver circuitos de resistencia. Para utilizar impedancias, debemos dominar los números complejos. Aunque la aritmética de los números complejos es matemáticamente más complicada que con los números reales, la mayor comprensión del comportamiento del circuito y la facilidad con la que los circuitos se resuelven con impedancias merece la pena el desvío. Pero lo que es más importante, el concepto de impedancia es fundamental para la ingeniería y la física, teniendo un alcance mucho más allá de los circuitos.