3.15: Métodos de Circuito Formal - Método Nodo
- Page ID
- 85487
- Este módulo describe cómo usar un método de circuito formal, el método de nodo, para “resolver” cualquier circuito.
- Se puede emplear un método formal cuando no se pueden usar reglas de simplificación estándar.
En algunos casos (complicados), no podemos usar las técnicas de simplificación, como las reglas de combinación en paralelo o en serie, para resolver la relación entrada-salida de un circuito. En otros módulos, escribimos relaciones v-i y leyes de Kirchoff al azar, resolviéndolas más en la intuición que en el procedimiento. Necesitamos un método formal que produzca un conjunto pequeño y fácil de ecuaciones que conduzcan directamente a la relación insumo-producto que buscamos. Una de esas técnicas es el método del nodo.
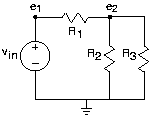
El método de nodo comienza por encontrar todos los nodos (lugares donde los elementos del circuito se unen entre sí) en el circuito. Llamamos a uno de los nodos el nodo de referencia; la elección del nodo de referencia es arbitraria, pero generalmente se elige para que sea un punto de simetría o el nodo “inferior”. Para los nodos restantes, definimos voltajes de nodo
En algunos casos, un voltaje de nodo corresponde exactamente al voltaje a través de una fuente de voltaje. En tales casos, la tensión del nodo es especificada por la fuente y no es desconocida. Por ejemplo, en nuestro circuito,
\[e_{1}=v_{in} \nonumber \]
Por lo tanto, solo necesitamos encontrar un voltaje de nodo.
Las ecuaciones que gobiernan los voltajes de los nodos se obtienen escribiendo ecuaciones KCL en cada nodo que tienen una tensión de nodo desconocida, usando las relaciones v-i para cada elemento. En nuestro ejemplo, la única ecuación de circuito es
\[\frac{e_{2}-v_{in}}{R_{1}}+\frac{e_{2}}{R_{2}}+\frac{e_{3}}{R_{3}}=0 \nonumber \]
Un poco de reflexión revela que al escribir las ecuaciones KCL para la suma de corrientes que salen de un nodo, el voltaje de ese nodo siempre aparecerá con un signo más, y todos los demás voltajes de nodo con un signo menos. La aplicación sistemática de este procedimiento facilita escribir ecuaciones de nodos y verificarlas antes de resolverlas. También recuerda revisar unidades en este punto: Cada término debe tener unidades de corriente. En nuestro ejemplo, resolver para el voltaje de nodo desconocido es fácil:
\[e_{2}=\frac{R_{2}R_{3}}{R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}}v_{in} \nonumber \]
¿Realmente hemos resuelto el circuito con el método node? En el camino, hemos utilizado las relaciones KVL, KCL y v-i. Anteriormente, indicamos que el conjunto de ecuaciones resultantes de aplicar estas leyes es necesario y suficiente. Este resultado garantiza que el método del nodo puede ser utilizado para “resolver” cualquier circuito. Una consecuencia de este resultado es que debemos poder encontrar cualquier variable de circuito dadas las tensiones y fuentes de los nodos. Todas las variables de circuito se pueden encontrar usando las relaciones v-i y el divisor de voltaje. Por ejemplo, la corriente a través de R 3 es igual a e 2/R 3.
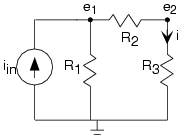
La presencia de una fuente de corriente en el circuito no afecta mucho al método del nodo; solo inclúyalo al escribir ecuaciones KCL como una corriente que sale del nodo. El circuito cuenta con tres nodos, requiriendo que definamos dos voltajes de nodo. Las ecuaciones de nodo son
\[\frac{e_{1}}{R_{1}}+\frac{e_{1}-e_{2}}{R_{2}}-i_{in}=0\; \; \; \; Node\; 1 \nonumber \]
\[\frac{e_{2}-e_{1}}{R_{2}}+\frac{e_{2}}{R_{3}}=0\; \; \; \; Node\; 2 \nonumber \]
Obsérvese que el voltaje del nodo correspondiente al nodo para el que estamos escribiendo KCL entra con un signo positivo, los otros con un signo negativo, y que las unidades de cada término se dan en amperios. Reescriba estas ecuaciones en la forma estándar de conjunto de ecuaciones lineales.
\[e_{1}\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}} \right )-e_{2}\frac{1}{R_{2}}=i_{in} \nonumber \]
\[e_{1}\frac{1}{R_{2}}+e_{2}\left ( \frac{1}{R_{2}}+\frac{1}{R_{3}} \right )=0 \nonumber \]
Resolver estas ecuaciones da
\[e_{1}=\frac{R_{2}+R_{3}}{R_{3}}e_{2} \nonumber \]
\[e_{2}=\frac{R_{1}R_{3}}{R_{1}+R_{2}+R_{3}}i_{in} \nonumber \]
Para encontrar la corriente indicada, simplemente usamos:
\[i=\frac{e_{2}}{R_{3}} \nonumber \]
Calcular los voltajes de los nodos en e 1 y e 2.
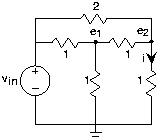
En el circuito anterior no podemos usar las reglas de combinación serie/paralelo: La resistencia vertical en el nodo 1 evita que las dos resistencias horizontales de 1 Ω estén en serie, y la resistencia de 2 Ω evita que las dos resistencias de 1 Ω en el nodo 2 estén en serie. ¡Realmente necesitamos el método de nodo para resolver este circuito! A pesar de tener seis elementos, solo necesitamos definir dos voltajes de nodo. Las ecuaciones de nodo son:
\[\frac{e_{1}-v_{in}}{1}+\frac{e_{1}}{1}+\frac{e_{1}-e_{2}}{1}=0\; \; \; \; Node\; 1 \nonumber \]
\[\frac{e_{2}-v_{in}}{2}+\frac{e_{2}}{1}+\frac{e_{2}-e_{1}}{1}=0\; \; \; \; Node\; 2 \nonumber \]
Resolver estas ecuaciones rinde:
\[e_{1}=\frac{6}{13}v_{in} \nonumber \]
\[e_{2}=\frac{5}{13}v_{in} \nonumber \]
La corriente de salida es igual a:
\[\frac{e_{2}}{1}=\frac{5}{13}v_{in} \nonumber \]
Una consecuencia desafortunada de usar los valores numéricos del elemento desde el principio es que se vuelve imposible verificar unidades mientras se configuran y resuelven ecuaciones.
¿Cuál es la resistencia equivalente que ve la fuente de voltaje?
Solución
Para encontrar la resistencia equivalente, necesitamos encontrar la corriente que fluye a través de la fuente de voltaje. Esta corriente es igual a la corriente que acabamos de encontrar más la corriente que fluye a través de la otra resistencia vertical de 1 Ω. Esta corriente es igual a:
\[e_{1}=\frac{6}{13}v_{in} \nonumber \]
haciendo que la corriente total a través de la fuente de voltaje (fluyendo fuera de ella)
\[\frac{11}{13}v_{in} \nonumber \]
Por lo tanto, la resistencia equivalente es
\[\frac{13}{11}\Omega \nonumber \]
Método de Nodo e Impedancias
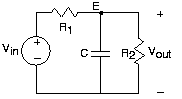
El método de nodo se aplica a los circuitos RLC, sin modificación significativa de los métodos utilizados en circuitos resistivos simples, si utilizamos amplitudes complejas. Nos basamos en el hecho de que amplitudes complejas satisfacen las relaciones KVL, KCL y v-i basadas en impedancia. En el circuito de ejemplo, definimos amplitudes complejas para las variables de entrada y salida y para las tensiones de los nodos. Aquí solo necesitamos un voltaje de nodo, y su ecuación KCL es:
\[\frac{E-V_{in}}{R_{1}}+Ei2\pi fC+\frac{E}{R_{2}}=0 \nonumber \]
con el resultado
\[E=\frac{R_{2}}{R_{1}+R_{2}+i2\pi fR_{1}R_{2}C}V_{in} \nonumber \]
Para encontrar la función de transferencia entre los voltajes de entrada y salida, calculamos la relación E/V in. La magnitud y el ángulo de la función de transferencia son:
\[\left | H(f) \right |=\frac{R_{2}}{\sqrt{(R_{1}+R_{2})^{2}+(2\pi fR_{1}R_{2}C)^{2}}} \nonumber \]
\[\angle (H(f))=-\arctan \left ( \frac{2\pi fR_{1}R_{2}C}{R_{1}+R_{2}} \right ) \nonumber \]
Este circuito difiere del mostrado anteriormente en que la resistencia R2 se ha agregado a través de la salida. Qué efecto ha tenido en la función de transferencia, que en el circuito original era un filtro de paso bajo que tenía frecuencia de corte:
\[f_{c}=\frac{1}{2\pi R_{1}C} \nonumber \]
Como se muestra en la Figura 3.15.5 a continuación, agregar la segunda resistencia tiene dos efectos: disminuye la ganancia en la banda de paso (el rango de frecuencias para las que el filtro tiene poco efecto en la entrada) y aumenta la frecuencia de corte.
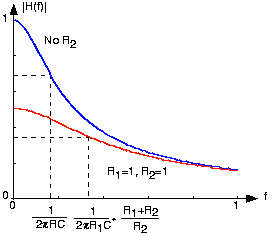
Aquí, R 1 =1, R 2 =1, C=1
Cuando R1 = R2 como se muestra en la gráfica, la ganancia de banda de paso se convierte en la mitad de la original, y la frecuencia de corte aumenta en el mismo factor. Por lo tanto, agregar R 2 proporciona una 'perilla' mediante la cual podemos intercambiar ganancia de banda de paso por frecuencia de corte.
Podemos cambiar la frecuencia de corte sin afectar la ganancia de banda de paso cambiando la resistencia en el circuito original. ¿La adición de la resistencia R 2 ayuda en el diseño del circuito?
Solución
No necesariamente, sobre todo si deseamos perillas individuales para ajustar la ganancia y la frecuencia de corte.


