3.21: Problemas de procesamiento de señales analógicas

Última actualización
Guardar como PDF

Page ID: 85522

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Problemas para tratar con el procesamiento de señales analógicas.

Análisis Sencillo de Circuitos

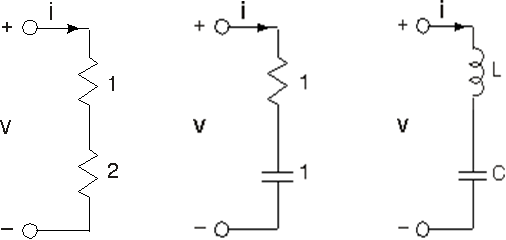
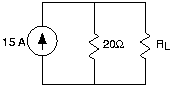
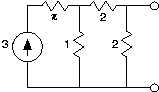
Para cada circuito mostrado en la Figura 3.21.1, la corriente

\[i=\cos (2\pi t) \nonumber \]

¿Cuál es el voltaje a través de cada elemento y cuál es el voltaje v en cada caso?
Para el último circuito, ¿hay valores de elementos que hagan que el voltaje v sea igual a cero para todos los tiempos? Si es así, ¿qué valores de elemento funcionan?
Nuevamente, para el último circuito, si fuera posible voltaje cero, ¿qué elemento de circuito podría sustituir a la combinación en serie de capacitor-inductor que produciría el mismo voltaje?

Resolviendo Circuitos Simples

Circuito A Circuito B

Figura 3.21.2

Escribe el conjunto de ecuaciones que gobiernan el comportamiento del Circuito A.
Resuelve estas ecuaciones para i ₁: En otras palabras, expresar esta corriente en términos de valores de elemento y fuente eliminando tensiones y corrientes que no son fuente.
Para el Circuito B, encuentra el valor para R _L que da como resultado que una corriente de 5A pase a través de él.
¿Cuál es la potencia disipada por la resistencia de carga R _L en este caso?

Resistencia Equivalente

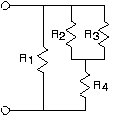
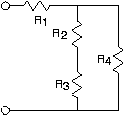
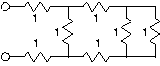
circuito a circuito b circuito c circuito d

Figura 3.21.3

Para cada uno de los circuitos anteriores, encuentra la resistencia equivalente usando reglas de combinación en serie y paralelo.
Calcular la conductancia vista en los terminales para el circuito (c) en términos de la conductancia de cada elemento.
Compare esta fórmula de conductancia equivalente con la fórmula de resistencia equivalente que encontró para el circuito (b).
¿Cómo se deriva el circuito (c) del circuito (b)?

Principio de superposición

Una de las consecuencias más importantes de las leyes de circuitos es el Principio de Superposición: La corriente o voltaje definido para cualquier elemento es igual a la suma de las corrientes o voltajes producidos en el elemento por las fuentes independientes. Este Principio tiene importantes consecuencias en la simplificación del cálculo de variables ciruit en múltiples circuitos fuente.

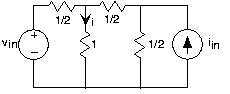
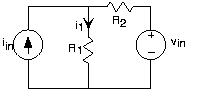
Para el circuito representado, encuentra la corriente indicada usando cualquier técnica que te guste (debes usar la más simple).

Debió haber encontrado que la corriente

Este resultado significa que podemos pensar en la corriente como una superposición de dos componentes, cada uno de los cuales se debe a una fuente. Podemos encontrar cada componente estableciendo las otras fuentes en cero. Así, para encontrar el componente de fuente de voltaje, puede establecer la fuente de corriente a cero (un circuito abierto) y usar los trucos habituales. Para encontrar el componente de fuente de corriente, establecería la fuente de voltaje en cero (un cortocircuito) y encontraría la corriente resultante. Calcular la corriente total

¿Es más fácil aplicar el Principio de Superposición que la técnica que utilizaste en la parte (1)?

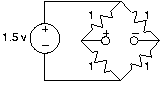
Divisor de corriente y voltaje

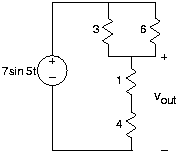
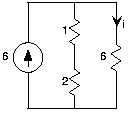
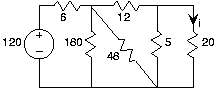
Utilice reglas de divisor de corriente o voltaje para calcular las variables de circuito indicadas en los circuitos de la Figura 3.21.5.

Equivalentes Thévenin y Mayer-Norton

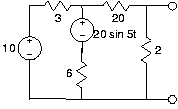
Encuentre los circuitos equivalentes Thévenin y Mayer-Norton para los circuitos en la Figura 3.21.6.

Trabajo Detective

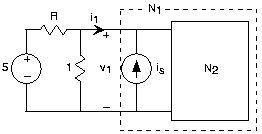
En el circuito de la Figura 3.21.7, el circuito N ₁ tiene la relación v-i:\[v_{1}=3i_{1}+7\; \; when\; \; i_{s}=2 \nonumber \]

Encuentra el circuito equivalente Thévenin para el circuito N ₂.
Con i _s =2 determinar R tal que i ₁ =-1.

Circuitos de puente

Los circuitos que tienen la forma de la Figura 3.21.8 se denominancircuitos puente.

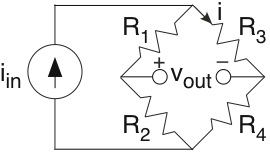
¿Qué resistencia ve la fuente de corriente cuando no hay nada conectado a los terminales de salida?
¿Qué valores de resistencia, si los hay, resultarán en un voltaje cero para v _out?
Supongamos R ₁ =1Ω, R ₂ =2Ω, R ₃ =2Ω, R ₄ =4Ω. Encuentra la corriente i cuando la fuente de corriente i _en es\[i_{in}=\Im \left ( \left ( 4+2i \right )e^{i2\pi 20t} \right ) \nonumber \] Expresar tu respuesta como sinusoide.

Conversión de Cartesiano a Polar

Convierte las siguientes expresiones en forma polar. Trazar su ubicación en el plano complejo.

\[(1+\sqrt{-3})^{2} \nonumber \]
\[3+i^{4} \nonumber \]
\[\frac{2-i\frac{6}{\sqrt{3}}}{2+i\frac{6}{\sqrt{3}}} \nonumber \]
\[(4-i^{3})(1+i\frac{1}{2}) \nonumber \]
\[3e^{i\pi }+4e^{i\frac{\pi }{2}} \nonumber \]
\[(\sqrt{3}+i)2\times \sqrt{2}e^{-(i\frac{\pi }{4})} \nonumber \]
\[\frac{3}{1+i3\pi } \nonumber \]

El Plano Complejo

La variable compleja z se relaciona con la variable real u según\[z=1+e^{iu} \nonumber \]

Dibuje el contorno de los valores que toma z en el plano complejo.
¿Cuáles son los valores máximos y mínimos alcanzables por |z|?
Dibuje el contorno de las\[\frac{z-1}{z+1} \nonumber \] trazas de la función racional en el plano complejo.

Curvas Frescas

En las siguientes expresiones, la variable x va de cero a infinito. ¿Qué formas geométricas trazan las siguientes en el plano complejo?

\[e^{ix} \nonumber \]
\[1+e^{ix} \nonumber \]
\[e^{-x}e^{ix} \nonumber \]
\[e^{ix}+e^{i(x+\frac{\pi }{4})} \nonumber \]

Identidades trigonométricas y exponenciales complejos

Mostrar las siguientes identidades trigonométricas utilizando exponenciales complejos. En muchos casos, se derivaron utilizando este enfoque.

\[\sin (2u)=2\sin (u)\cos (u) \nonumber \]
\[\cos ^{2}(u)=\frac{1+\cos (2u)}{2} \nonumber \]
\[\cos ^{2}(u)+\sin ^{2}(u)=1 \nonumber \]
\[\frac{\mathrm{d} }{\mathrm{d} u}\left ( \sin (u) \right )=\cos (u) \nonumber \]

Funciones de transferencia

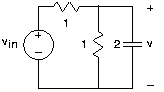
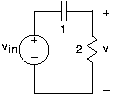
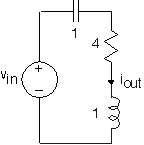
Encuentre la función de transferencia que relaciona las amplitudes complejas de la variable indicada y la fuente mostrada en la Figura 3.21.9. Trazar la magnitud y fase de la función de transferencia.

Uso de Impedancias

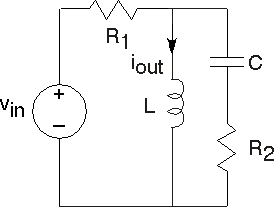
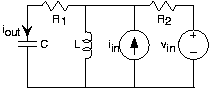
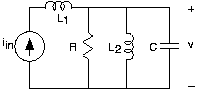
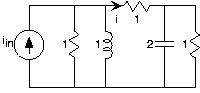
Encuentra la ecuación diferencial que relaciona la variable indicada con la (s) fuente (s) usando impedancias para cada circuito mostrado en la Figura 3.21.10

Caos de Medición

Se construyó el circuito simple en la Figura 3.21.11 pero las mediciones de la señal se hicieron al azar.

Cuando la fuente fue:

\[\sin (2\pi f_{0}t) \nonumber \]

la corriente:

\[i(t)=\frac{\sqrt{2}}{3}\sin (2\pi f_{0}t+\frac{\pi }{4}) \nonumber \]

el voltaje:

\[v_{2}(t)=\frac{1}{3}\sin (2\pi f_{0}t) \nonumber \]

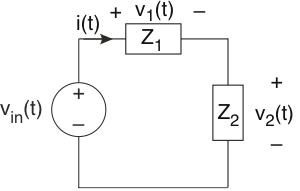
¿Cuál es el voltaje v ₁ (t)?
Encuentra las impedancias Z ₁ y Z ₂.
Construir estas impedancias a partir de elementos elementales del circuito.

Funciones de transferencia

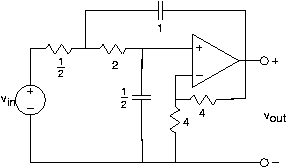
En el circuito de la Figura 3.21.12, la fuente de voltaje es igual a:

\[v_{in}(t)=10\sin \left ( \frac{t}{2}\right ) \nonumber \]

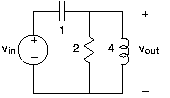
Encuentre la función de transferencia entre la fuente y el voltaje de salida indicado.
Para la fuente dada, encuentre el voltaje de salida.

Un circuito simple

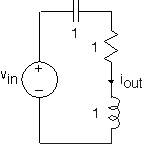
En el circuito simple de la Figura 3.21.13,

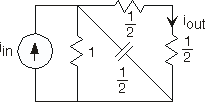
¿Cuál es la función de transferencia entre la fuente y la corriente de salida indicada?
Si la corriente de salida se mide para que sea Cos (2t), ¿cuál fue la fuente?

Diseño de circuitos

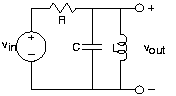
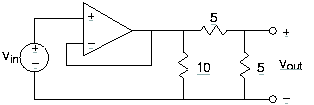
Encuentre la función de transferencia entre los voltajes de entrada y salida para los circuitos mostrados en la Figura 3.21.14.
¿A qué frecuencia tiene la función de transferencia un desplazamiento de fase de cero? ¿Cuál es la ganancia del circuito a esta frecuencia?
Las especificaciones exigen que este circuito tenga una impedancia de salida (su impedancia equivalente) inferior a 8Ω para frecuencias superiores a 1 kHz, la frecuencia a la que la función de transferencia es máxima. Encuentra valores de elementos que satisfagan este criterio.

Circuitos Equivalentes y Potencia

Supongamos que tenemos un circuito arbitrario de resistencias que colapsamos en una resistencia equivalente usando las reglas en serie y paralelas. ¿La potencia disipada por la resistencia equivalente es igual a la suma de las potencias disipadas por las resistencias reales que componen el circuito? Comencemos con casos simples y construyamos hasta una prueba completa.

Supongamos que las resistencias _R1 y _R2 están conectadas en paralelo. Mostrar que la potencia disipada por R ₁ | | _R2 es igual a la suma de las potencias disipadas por las resistencias componentes.
Ahora supongamos que R ₁ y _R2 están conectados en serie. Muestra el mismo resultado para esta combinación.
Utilice estos dos resultados para probar el resultado general que buscamos.

Transmisión de Potencia

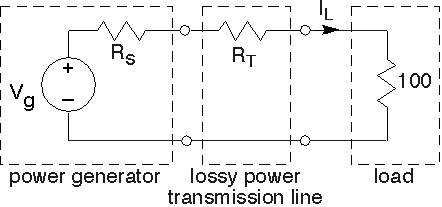
La red mostrada en la Figura 3.21.15 representa un sistema simple de transmisión de potencia. El generador produce 60 Hz y es modelado por un simple equivalente Thévenin. La línea de transmisión consiste en una larga longitud de cable de cobre y se puede describir con precisión como una resistencia de 50Ω.

Transmisión de Potencia Simple Circuito de carga modificado

Figura 3.21.15

Determinar la corriente de carga R _L y la potencia promedio que debe producir el generador para que la carga reciba 1,000 watts de potencia promedio.
¿Por qué el generador necesita generar más de 1,000 vatios de potencia promedio para cumplir con este requisito?
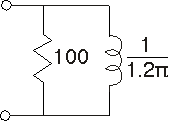
Supongamos que la carga se cambia a la que se muestra en la figura para Circuito de carga modificada. Ahora, ¿cuánta energía debe producir el generador para cumplir con el mismo requisito de energía? ¿Por qué es más de lo que tenía que producir para cumplir con el requisito de la carga resistiva?
La carga se puede compensar para tener un factor de potencia unitaria (ver ejercicio) para que el voltaje y la corriente estén en fase para lograr la máxima eficiencia energética. La técnica de compensación consiste en colocar un circuito en paralelo al circuito de carga. ¿Qué elemento funciona y cuál es su valor?
Con este circuito compensado, ¿cuánta energía debe producir el generador para entregar 1,000 de potencia promedio a la carga?

Transmisión de Potencia Óptima

La Figura 3.21.16 muestra un modelo general para transmisión de potencia. El generador de energía está representado por un equivalente Thévinin y la carga por una simple impedancia. En la mayoría de las aplicaciones, los componentes de origen son fijos mientras que hay cierta latitud en la elección de la carga.

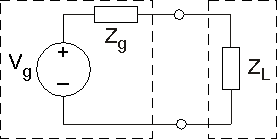
Supongamos que queríamos maximizar la “transmisión de voltaje”: hacer que el voltaje a través de la carga sea lo más grande posible. ¿Qué elección de impedancia de carga crea el mayor voltaje de carga? ¿Cuál es el voltaje de carga más grande?
Si quisiéramos que la corriente máxima pasara a través de la carga, ¿cuál elegiríamos que fuera la impedancia de carga? ¿Cuál es esta corriente más grande?
¿Qué opción para la impedancia de carga maximiza la potencia promedio disipada en la carga? ¿Cuál es la mayor cantidad de energía que puede entregar el generador?

Nota

Una forma de maximizar una función de una variable compleja es escribir la expresión en términos de las partes real e imaginaria de la variable, evaluar las derivadas con respecto a cada una, establecer ambas derivadas a cero y resolver las dos ecuaciones simultáneamente.

Grande es hermoso

Sammy quiere elegir altavoces que produzcan música muy fuerte. Tiene un amplificador y nota que los terminales de los altavoces están etiquetados como “fuente 8Ω”.

¿Qué significa esto en términos del circuito equivalente del amplificador?
Cualquier altavoz que Sammy se conecte a los terminales puede ser bien modelado como una resistencia. Elegir un altavoz equivale a elegir los valores para la resistencia. ¿Qué opción maximizaría el voltaje a través de los altavoces?
Sammy decide que maximizar la potencia entregada al altavoz podría ser una mejor opción. ¿Qué valores para la resistencia del altavoz deben elegirse para maximizar la potencia entregada al altavoz?

Compartir un canal

Dos pares transmisor-receptor quieren compartir el mismo canal de comunicaciones digitales. Las señales del transmisor se sumarán juntas por el canal. El diseño del receptor se simplifica enormemente si primero eliminamos la transmisión no deseada (tanto como sea posible). Cada señal del transmisor tiene la forma:

\[\forall t,\; 0\leq t\leq T:\; \left ( x_{i}(t)=A\sin (2\pi f_{i}t) \right ) \nonumber \]

donde la amplitud es cero o A y cada transmisor utiliza su propia frecuencia f _i. Cada frecuencia está relacionada armónicamente con la duración del intervalo de bits T, donde el transmisor 1 utiliza la frecuencia 1/T. La velocidad de datos es de 10 Mbps.

Dibuja un diagrama de bloques que exprese este escenario de comunicación.
Encuentra circuitos que los receptores podrían emplear para separar las transmisiones no deseadas. Supongamos que la señal recibida es una tensión y la salida debe ser una tensión también.
Encuentra la frecuencia del segundo transmisor para que los receptores puedan suprimir la transmisión no deseada en al menos un factor de diez.

Trabajo de Detective de Circuito

En el laboratorio, el voltaje de circuito abierto medido a través de los terminales de un circuito desconocido es igual a sin (t). Cuando se coloca una resistencia de 1Ω a través de los terminales, aparece un voltaje que tiene el siguiente valor:

\[v(t)=\frac{1}{\sqrt{2}}\sin \left ( t+\frac{\pi }{4} \right ) \nonumber \]

¿Qué es el circuito equivalente Thévenin?
¿Qué voltaje aparecerá si colocamos un condensador de 1F a través de los terminales?

Circuito Misterioso

Queremos determinar tanto como podamos sobre el circuito que acecha en la caja impenetrable que se muestra en la Figura 3.21.17. Se ha conectado una fuente de voltaje v _in =2V a los terminales izquierdos, dejando los terminales correctos para pruebas y mediciones.

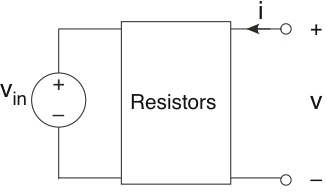
Sammy mide V=10V cuando una resistencia de 1 Ω está conectada a los terminales. Samantha dice que se equivoca. ¿Quién está en lo correcto y por qué?
Cuando no hay nada conectado a los terminales de la derecha, se mide un voltaje de V=1V. ¿Qué circuito podría producir esta salida?
Cuando se conecta una fuente de corriente de manera que I=2a, el voltaje v es ahora de 3 V. ¿Qué circuito de resistencia sería consistente con esta y la parte anterior?

Más Trabajo de Detective de Circuito

El par de terminales izquierdo de un circuito de dos pares terminales en la Figura 3.21.18 está conectado a un circuito de prueba. La fuente de prueba

\[v_{in}(t)=\sin (t) \nonumber \]

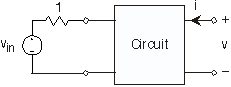
Realizamos las siguientes medidas:

Sin nada conectado a los terminales de la derecha, el voltaje\[v(t)=\frac{1}{\sqrt{2}}\cos \left ( t+\frac{\pi }{4} \right ) \nonumber \]
Cuando se coloca un cable a través de los terminales de la derecha, la corriente\[i(t)=-\sin (t) \nonumber \]

¿Cuál es la impedancia “vista” de los terminales de la derecha?
Encuentre el voltaje v (t) si una fuente de corriente está conectada a los terminales de la derecha para que\[i(t)=\sin (t) \nonumber \]

Lineales, Sistemas invariantes en el tiempo

Para que un sistema se caracterice completamente por una función de transferencia, no solo necesita ser lineal, sino también ser invariable en el tiempo. Se dice que un sistema es invariable en el tiempo si retrasar la entrada retrasa la salida en la misma cantidad. Matemáticamente, si

\[S\left ( x(t) \right )=y(t) \nonumber \]

lo que significa que y (t) es la salida de un sistema S (•) cuando x (t) es la entrada, S (•) es la invariante de tiempo si:

\[S\left ( x(t-\tau ) \right )=y(t-\tau ) \nonumber \]

para todos los retardos τ y todas las entradas x (t). Tenga en cuenta que tanto los sistemas lineales como los no lineales tienen esta propiedad. Por ejemplo, un sistema que cuadra su entrada es invariable en el tiempo.

Mostrar que si un circuito tiene elementos de circuito fijos (sus valores no cambian con el tiempo), su relación entrada-salida es invariable en el tiempo. Pista: Considere la ecuación diferencial que describe la relación entrada-salida de un circuito. ¿Cuál es su forma general? Examine la (s) derivada (s) de las señales retardadas.
Mostrar que las impedancias no pueden caracterizar elementos de circuito variables en el tiempo (R, L y C). En consecuencia, muestran que los sistemas lineales y variables en el tiempo no tienen una función de transferencia.
Determinar la linealidad e invarianza temporal de lo siguiente. Encuentre la función de transferencia del uno (s) lineal, invariable en el tiempo (LTI).
1. \[y(t)=x(t)\sin (2\pi f_{0}t) \nonumber \]
2. \[y(t)=x(t-\tau _{0}) \nonumber \]
3. \[y(t)=x(t)+N(t) \nonumber \]

Noches Largas e Indormidas

Sammy fue al laboratorio después de una larga noche sin dormir, y construyó el circuito que se muestra en la Figura 3.21.19. No puede recordar cuál era el circuito, representado por la impedancia Z. Claramente, este circuito olvidado es importante ya que la salida es la corriente que pasa por él.

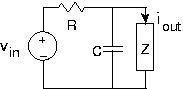
¿Cuál es el circuito equivalente Thévenin visto por la impedancia?
Al buscar sus notas, Sammy encuentra que el circuito es realizar la función de transferencia:\[H(f)=\frac{1}{i10\pi f+2} \nonumber \] Encuentra la impedancia

Un circuito de prueba

El circuito simple como se muestra en la Figura 3.21.20 se dio en una prueba.

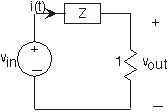
Cuando la fuente de voltaje es:

\[v_{in}(t)=\sqrt{5}\sin (t) \nonumber \]

la corriente es:

\[i(t)=\sqrt{2}\cos \left ( t-\arctan (2)-\frac{\pi }{4} \right ) \nonumber \]

¿Qué es el voltaje v _out (t)?
¿Cuál es la impedancia Z a la frecuencia de la fuente?

Circuito de caja negra

Se le da un circuito que se muestra en la Figura 3.21.21 que tiene dos terminales para unir elementos de circuito.

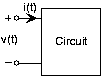
Cuando conecta una fuente de voltaje igual a sin (t) a los terminales, la corriente a través de la fuente es igual a:

\[i(t)=4\sin \left ( t+\frac{\pi }{4} \right )-2\sin (4t) \nonumber \]

Cuando no hay ninguna fuente conectada (terminales de circuito abierto), el voltaje a través de los terminales tiene la forma:

\[v(t)=A\sin (4t+\varphi ) \nonumber \]

¿Cuál será la corriente del terminal cuando reemplace la fuente por un cortocircuito?
Si fueras a construir un circuito que fuera idéntico (desde el punto de vista de los terminales) al dado, ¿cuál sería tu circuito?
Para tu circuito, ¿qué son A y φ? 3sin (t)

Resolviendo un circuito misterioso

Sammy debe determinar todo lo que pueda sobre un circuito misterioso conectando elementos al terminal y midiendo el voltaje resultante. Cuando conecta una resistencia de 1Ω a los terminales del circuito, mide el voltaje a través de los terminales para que sea 3sin (t). Cuando conecta un condensador 1F a través de los terminales, el voltaje es ahora:

\[3\times \sqrt{2}\sin \left ( t-\frac{\pi }{4} \right ) \nonumber \]

¿Qué voltaje debe medir cuando no conecta nada al circuito misterioso?
¿Qué voltaje debe medir Sammy si duplicó el tamaño del condensador a 2 F y lo conectó al circuito?

Encuentre la Impedancia de Carga

El circuito en la Figura 3.21.22 tiene una función de transferencia entre el voltaje de salida y la fuente igual a

\[H(f)=\frac{-8\pi ^{2}f^{2}}{8\pi ^{2}f^{2}+4+i6\pi f} \nonumber \]

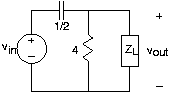
Esbozar la magnitud y fase de la función de transferencia.
¿A qué frecuencia la fase es igual a π/2?
Encuentra un circuito que corresponda a esta impedancia de carga. ¿Tu respuesta es única? Si es así, demuéstralo para que sea así; si no, dar otro ejemplo.

Rechazo analógico “Hum”

“Hum” se refiere a la corrupción de la toma de corriente de pared que frecuentemente se cuela en los circuitos. “Hum” recibe su nombre porque suena como un zumbido persistente. Queremos encontrar un circuito que elimine el zumbido de cualquier señal. Un ingeniero sugiere usar un circuito divisor de voltaje simple que consta de dos impedancias en serie como se muestra en la Figura 3.21.23 a continuación.

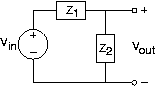
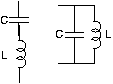
La impedancia Z ₁ es una resistencia. El ingeniero deberá decidir entre los dos circuitos mostrados en la otra figura para la impedancia Z ₂. ¿Cuál de estos va a funcionar?
Escogiendo un circuito que funcione, elija valores de elementos de circuito que eliminen el zumbido.
Esbozar la magnitud de la respuesta de frecuencia resultante.

Un Circuito Interesante

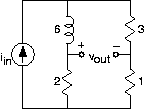
Para el circuito que se muestra en la Figura 3.21.24, encuentre la función de transferencia.
Cuál es el voltaje de salida cuando la entrada tiene la forma:\[i_{in}=5\sin (2000\pi t) \nonumber \]

Un circuito simple

Consulte el circuito en la Figura 3.21.25.

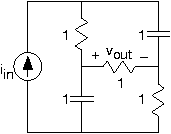
¿Cuál es la función de transferencia entre la fuente y la tensión de salida?
¿Cuál será el voltaje cuando la fuente sea igual a sin (t)?
Muchos generadores de funciones producen un desplazamiento constante además de una sinusoide. Si la fuente es igual a 1+ sin (t), ¿cuál es el voltaje de salida?

Un Circuito Interesante y Útil

El circuito de la Figura 3.21.26 tiene propiedades interesantes, las cuales son explotadas en osciloscopios de alto rendimiento.

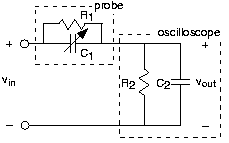
La porción del circuito etiquetada como “Osciloscopio” representa la impedancia de entrada del alcance. R ₂ =1MΩ y C ₂ =30pF (anote la etiqueta debajo de la entrada del canal 1 en los osciloscopios del laboratorio). Una sonda es un dispositivo para conectar un osciloscopio a un circuito, y tiene el circuito indicado dentro de él.

Supongamos por un momento que la sonda es meramente un cable y que el osciloscopio está unido a un circuito que tiene una impedancia resistiva equivalente a Thévenin. ¿Cuál sería el efecto de la impedancia de entrada del osciloscopio sobre los voltajes medidos?
Usando el método de nodo, encuentre la función de transferencia que relaciona el voltaje indicado con la fuente cuando se usa la sonda.
Trazar la magnitud y fase de esta función de transferencia cuando _R1 =9Ω y C ₁ =2pF.
Para una relación particular entre los valores de los elementos, la función de transferencia es bastante simple. Encuentra esa relación y describe lo que tiene de especial.
La flecha a través de _C1 indica que su valor se puede variar. Seleccione el valor de este condensador para que la relación especial sea válida. ¿Cuál es la impedancia que ve el circuito que se mide para este valor especial?

Un problema en el circuito

Se le da un circuito como se muestra en la Figura 3.21.27.

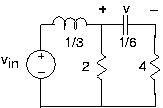
Encuentre la ecuación diferencial que relaciona el voltaje de salida con la fuente.
¿Cuál es la impedancia “vista” por el condensador?

Computadoras Analógicas

Debido a que las ecuaciones diferenciales que surgen en los circuitos se asemejan a las que describen el movimiento mecánico, podemos usar modelos de circuitos para describir sistemas mecánicos. Un alumno ELEC 241 quiere entender el sistema de suspensión en su auto. Sin suspensión, la carrocería del auto se mueve en concierto con los baches en el raod. Un sistema de suspensión bien diseñado suavizará las carreteras con baches, reduciendo el movimiento vertical del automóvil. Si los baches son muy graduales (piense en una colina como un bache grande pero muy gradual), el movimiento vertical del automóvil debería seguir el de la carretera. El alumno quiere encontrar un circuito sencillo que modele el movimiento del auto. Está tratando de decidir entre dos modelos de circuito como se muestra en la Figura 3.21.28.

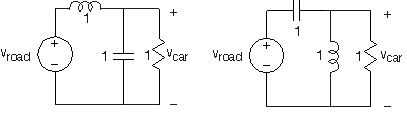
Aquí, los desplazamientos de carretera y automóvil están representados por los voltajes v _road (t) y v _car (t) respectivamente.

¿Qué circuito elegirías? ¿Por qué?
Para el circuito que escogiste, cuál será la amplitud del movimiento del auto si la carretera tiene un desplazamiento dado por:\[v_{road}(t)=1+\sin (2t) \nonumber \]

Funciones de transferencia y circuitos

Se le da el circuito en la Figura 3.21.29.

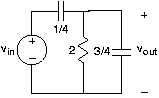
Encuentra la función de transferencia entre V _in y V _out.
Esboce la magnitud y la fase de su función de transferencia. Etiquetar valores importantes de frecuencia, amplitud y fase.
_{Averiguar v hacia fuera} (t) cuando\[v_{in}(t)=\sin \left ( \frac{t}{2}+\frac{\pi }{4} \right ) \nonumber \]

Diversión en el laboratorio

Se te da una caja no abrible que tiene dos terminales sobresaliendo. Asume que la caja contiene un circuito. Se mide el voltaje

\[v(t)=\sin \left ( t+\frac{\pi }{4} \right ) \nonumber \]

a través de los terminales cuando no hay nada conectado a ellos y la corriente

\[i(t)=\sqrt{2}\cos (t) \nonumber \]

cuando coloca un cable a través de los terminales.

Encuentra un circuito que tenga estas características.
Se conecta un inductor de 1 H a través de los terminales. ¿Qué voltaje mide?

Fuentes Dependientes

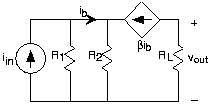
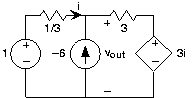
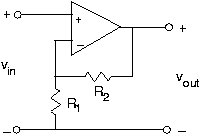
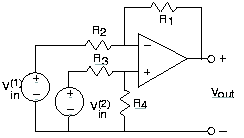
Encuentra el voltaje v _out en cada uno de los circuitos en la Figura 3.21.30.

Amplificadores Operacionales

Amplificador operacional a Amplificador operacional b

Amplificador operacional c Amplificador operacional d

Figura 3.21.31

Encuentre la función de transferencia entre la (s) tensión (es) de fuente y la tensión de salida indicada para los circuitos mostrados en la Figura 3.21.31.

Circuito Op-Amp

El circuito si se afirma que la Figura 3.21.32 tiene un propósito útil.

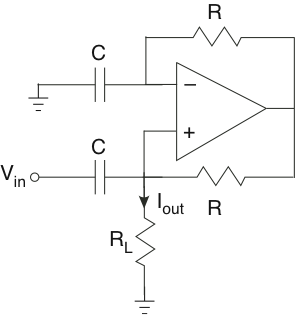
¿Cuál es la función de transferencia que relaciona la amplitud compleja de la señal de salida, la corriente I _out _, con la amplitud compleja de la entrada, la tensión V _in?
¿Qué circuito equivalente ve la resistencia de carga R _L?
Encuentre la corriente de salida cuando\[v_{in}=V_{0}e^{-\frac{t}{\tau }} \nonumber \]

Por qué son útiles los amplificadores operacionales

El circuito en la Figura 3.21.33 es una cascada de circuitos op-amp que ilustra la razón por la cual las realizaciones de op-amp de funciones de transferencia son tan útiles.

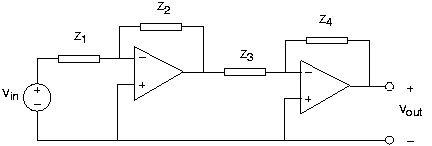
Encuentre la función de transferencia que relaciona la amplitud compleja de la tensión v _out (t) con la fuente. Demostrar que esta función de transferencia es igual al producto de la función de transferencia de cada etapa.
¿Cuál es la impedancia de carga que aparece en la salida del primer amplificador operacional?
La Figura 3.21.34 a continuación ilustra que a veces los “diseños” pueden salir mal. Encuentre la función de transferencia para este circuito de amplificador operacional y luego demuestre que no puede funcionar! ¿Por qué no puede?

Amplificadores Operacionales

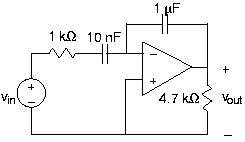
Considera el circuito en la Figura 3.21.35.

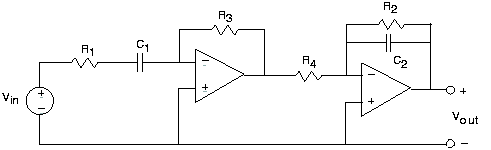
Encuentre la función de transferencia que relaciona el voltaje v _out (t) con la fuente.
R ₁ =530Ω, C ₁ =1µF, R ₂ =5.3KΩ, C ₂ =0.01µF, R ₃ =R ₄ =5.3KΩ. Caracterizar la función de transferencia resultante y determinar qué uso podría tener este circuito.

Diseño de un filtro de paso de banda

Queremos diseñar un filtro de paso de banda que tenga la función de transferencia

\[H(f)=10\frac{i2\pi f}{\left ( i\frac{f}{f_{l}}+1 \right )\left ( i\frac{f}{f_{h}}+1\right )} \nonumber \]

Aquí, f _l es la frecuencia de corte del borde de baja frecuencia de la banda de paso y f _h es la frecuencia de corte del borde de alta frecuencia.

Queremos f _l = 1kHz y f _h = 10kHz.

Trazar la magnitud y fase de esta respuesta de frecuencia. Etiquetar valores importantes de amplitud y fase y las frecuencias a las que ocurren.
Diseñe un filtro de paso de banda que cumpla con estas especificaciones. Especifique los valores de los componentes.

¿Pre-énfasis o de-énfasis?

En aplicaciones de audio, antes de la conversión analógico-digital las señales se pasan a través de lo que se conoce como un circuito de pre-énfasis que deja solas las bajas frecuencias pero proporciona ganancia creciente a frecuencias cada vez más altas más allá de alguna frecuencia f ₀. Los circuitos de desénfasis hacen lo contrario y se aplican después de la conversión digital a analógica. Después de pre-énfasis, digitalización, conversión de nuevo a analógico y de-énfasis, el espectro de la señal debería ser lo que era.

El circuito op-amp en la Figura 3.21.36 ha sido diseñado para pre-énfasis o de-énfasis (Samantha no puede recordar cuál).

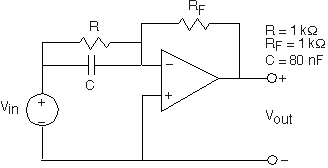
¿Es este un circuito de pre-énfasis o de-énfasis? Encuentra la frecuencia f ₀ que define la transición de frecuencias bajas a altas.
¿Cuál es la salida del circuito cuando el voltaje de entrada es sin (2 πft), con f=4kHz?
¿Qué circuito podría realizar la función opuesta a tu respuesta para la primera parte?

Filtro Activo

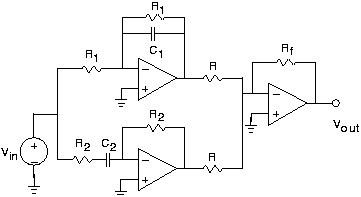
Encuentra la función de transferencia del filtro activo en la Figura 3.21.37.

¿Esto es un filtro?

Considera el circuito en la Figura 3.21.38.

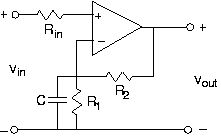
¿Cuál es la función de transferencia de este circuito? Trazar la magnitud y la fase.
Si la señal de entrada es la sinusoide sin (2 πf ₀ t), ¿cuál será la salida cuando f ₀ sea mayor que la “frecuencia de corte” del filtro?

Receptores Ópticos

En su teléfono óptico, el circuito receptor tenía la forma que se muestra en la Figura 3.21.39.

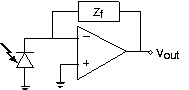
Este circuito sirvió como transductor, convirtiendo la energía de la luz en una _salida de voltaje v. El fotodiodo actúa como fuente de corriente, produciendo una corriente proporcional a la intesidad lumínica que cae sobre él. Como suele ser el caso en esta etapa crucial, las señales son pequeñas y el ruido puede ser un problema. Por lo tanto, la etapa op-amp sirve para aumentar la señal y para filtrar el ruido fuera de banda.

Encuentre la función de transferencia que relaciona la intensidad de la luz con v _out.
¿Cuál debería ser el circuito que realiza la impedancia de realimentación _Zf para que el transductor actúe como un filtro de paso bajo de 5 kHz?
Un ingeniero inteligente sugiere un circuito alternativo en la Figura 3.21.40 a continuación para lograr la misma tarea. Determinar si la idea funciona o no. Si lo hace, encuentre la impedancia Z _en la que logre la tarea de filtrado de paso bajo. Si no, muestra por qué no funciona.

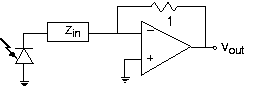
Ingeniería inversa

El circuito en la Figura 3.21.41 ha sido desarrollado por el grupo de diseño TBBG Electronics. Están tratando de mantener su uso en secreto; nosotros, representando a RU Electronics, hemos descubierto el esquema y queremos averiguar la aplicación pretendida. Supongamos que el diodo es ideal.

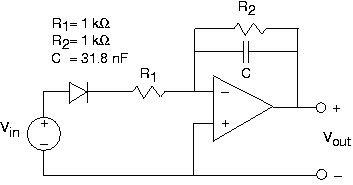
Suponiendo que el diodo es un cortocircuito (se ha eliminado del circuito), ¿cuál es la función de transferencia del circuito?
Con el diodo en su lugar, ¿cuál es la salida del circuito cuando el voltaje de entrada es sin (2 πf ₀ t)?
¿Qué función podría tener este circuito?