5.2: Introducción a la Organización de la Computación

Objetivos de aprendizaje

• Explica cómo los sistemas digitales como la computadora representan los números.
• Cubre los conceptos básicos del álgebra booleana y las matemáticas binarias.

Arquitectura de Computadoras

Para entender los sistemas de procesamiento de señales digitales, debemos entender un poco sobre cómo computan las computadoras. La definición moderna de una computadora es un dispositivo electrónico que realiza cálculos sobre datos, presentando los resultados a humanos u otras computadoras en una variedad de formas (ojalá útiles).

Figura 5.2.1 Organización genérica de hardware informático

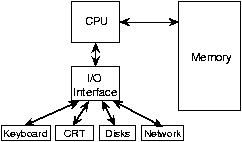
La computadora genérica contiene dispositivos de entrada (teclado, ratón, convertidor A/D (analógico a digital), etc.), una unidad computacional y dispositivos de salida (monitores, impresoras, convertidores D/A). La unidad computacional es el corazón de la computadora, y generalmente consiste en una unidad central de procesamiento (CPU), una memoria y una interfaz de entrada/salida (I/O). Los dispositivos de E/S que pueden estar presentes en una computadora determinada varían mucho.

• Una computadora simple opera fundamentalmente en tiempo discreto. Las computadoras son dispositivos cronometrados, en los que los pasos computacionales ocurren periódicamente de acuerdo con ticks de un reloj. Esta descripción desmiente la velocidad del reloj: Cuando dices “tengo una computadora de 1 GHz”, te refieres a que tu computadora tarda 1 nanosegundo en realizar cada paso. ¡Eso es increíblemente rápido! Un “paso” no significa, desafortunadamente, necesariamente un cálculo como una adición; las computadoras descomponen dichos cálculos en varias etapas, lo que significa que la velocidad del reloj no necesita expresar la velocidad computacional. La velocidad computacional se expresa en unidades de millones de instrucciones/segundo (Mips). Su computadora de 1 GHz (velocidad de reloj) puede tener una velocidad computacional de 200 Mips.
• Las computadoras realizan cálculos enteros (de valor discreto). Los cálculos informáticos pueden ser numéricos (obedeciendo las leyes de la aritmética), lógicos (obedeciendo las leyes de un álgebra) o simbólicos (obedeciendo cualquier ley que te guste). ¹ Cada instrucción de computadora que realiza un cálculo numérico elemental —una suma, una multiplicación o una división— lo hace solo para números enteros. La suma o producto de dos enteros también es un número entero, pero es probable que el cociente de dos enteros no sea un número entero. ¿Cómo maneja una computadora los números que tienen dígitos a la derecha del punto decimal? Este problema se aborda utilizando la llamada representación en coma flotante de números reales. En su esencia, sin embargo, esta representación se basa en cálculos de valor entero.

Representando números

Centrándose en los números, todos los números pueden ser representados por el sistema de notación posicional. ² El sistema de representación posicional b -aria utiliza la posición de dígitos que van de 0 a b -1 para denotar un número. La cantidad b se conoce como la base del sistema de números. Matemáticamente, los sistemas posicionales representan el entero positivo n como:

\[\forall d_{k},d_{k}\in \left \{ 0,...,b-1 \right \}:\left ( n=\sum_{k=0}^{\infty } d_{k}b^{k} \right ) \nonumber \]

y expresamos sucintamente n en base- b como:

\[n_{b}=d_{N}d_{N-1}...d_{0} \nonumber \]

El número 25 en la base 10 es igual a:

\[2\times 10^{1}+5\times 10^{0} \nonumber \]

De manera que los dígitos que representan este número son:

\[d_{0}=5,\; d_{1}=2\; all\; other\; d_{k}=0 \nonumber \]

Este mismo número en binario (base 2) es igual a:

\[11001(1\times 2^{4}+1\times 2^{3}+0\times 2^{2}+0\times 2^{1}+1\times 2^{0}) \nonumber \]

y 19 en hexadecimal (base 16). Las fracciones entre cero y uno se representan de la misma manera.

\[\forall d_{k},d_{k}\in \left \{ 0,...,b-1 \right \}:\left ( f=\sum_{k=-\infty }^{-1} d_{k}b^{k} \right ) \nonumber \]

Todos los números pueden ser representados por su signo, entero y partes fraccionarias. Los números complejos pueden considerarse como dos números reales que obedecen reglas especiales para manipularlos.

Los humanos usan la base 10, comúnmente se supone que se debe a que tenemos diez dedos. Las computadoras digitales utilizan la base 2 o representación numérica binaria, cada dígito de los cuales se conoce como un bit (b inary dig it).

Figura 5.2.2 Se ilustran las diversas formas en que los números se representan en binario. El número de bytes para los componentes exponente y mantisa de los números de punto flotante varía.

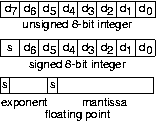
Aquí, cada bit se representa como un voltaje que es “alto” o “bajo”, representando así “1" o “0”, respectivamente. Para representar valores firmados, pegamos un bit especial, el bit de signo, para expresar el signo. La memoria de la computadora consiste en una secuencia ordenada de bytes, una colección de ocho bits. Por lo tanto, un byte puede representar un número sin signo que va de 0 a 255. Si tomamos uno de los bits y lo hacemos el bit de signo, podemos hacer el mismo byte para representar números que van desde -128 hasta 127. Pero una computadora no puede representar todos los números reales posibles. La falla no es con el sistema de números binarios; más bien tener solo un número finito de bytes es el problema. Si bien un gigabyte de memoria puede parecer mucho, se necesita un número infinito de bits para representar π. Como queremos almacenar muchos números en la memoria de una computadora, estamos restringidos a aquellos que tienen una representación binaria finita. Los enteros grandes se pueden representar por una secuencia ordenada de bytes. Las longitudes comunes, generalmente expresadas en términos del número de bits, son 16, 32 y 64. Así, un número de 32 bits sin signo puede representar enteros que oscilan entre 0 y 2 ³² -1 (4,294,967.295), ¡un número casi lo suficientemente grande como para enumerar a todos los humanos del mundo! ³

Ejercicio\(\PageIndex{1}\)

Tanto para representaciones enteras de 32 bits como de 64 bits, cuáles son los números más grandes que se pueden representar si también se debe incluir un bit de signo.

Solución

Para los enteros con signo de b bits, el número más grande es 2 ^b-1 - 1. Para b=32, tenemos 2,147,483,647 y para b=64, tenemos 9,223,372,036,854,775,807 o aproximadamente 9.2×10 ¹⁸.

Si bien este sistema representa bien los enteros, ¿qué tal los números que tienen dígitos distintos de cero a la derecha del punto decimal? En otras palabras, ¿cómo se representan los números que tienen partes fraccionarias? Para tales números, se utiliza el sistema de representación binaria, pero con un poco más de complejidad. El sistema de punto flotante utiliza un número de bytes - típicamente 4 u 8 - para representar el número, pero con un byte (a veces dos bytes) reservado para representar al exponente

\[x=m2^{^{e}} \nonumber \]

La mantisa generalmente se toma como una fracción binaria que tiene una magnitud en el rango

\[\left [ \frac{1}{2},1\right ) \nonumber \]

lo que significa que la representación binaria es tal que

\[d_{-1}=1 \nonumber \]

⁴ El número cero es una excepción a esta regla, y es el único número de punto flotante que tiene una fracción cero. El signo de la mantisa representa el signo del número y el exponente puede ser un entero con signo.

La representación de números enteros de una computadora es perfecta o solo aproximada, esta última situación ocurre cuando el entero excede el rango de números que un conjunto limitado de bytes puede representar. Las representaciones de punto flotante tienen problemas de representación similares: si el número

Ejercicio\(\PageIndex{1}\)

¿Cuáles son los números más grandes y más pequeños que se pueden representar en coma flotante de 32 bits? en punto flotante de 64 bits que tiene dieciséis bits asignados al exponente? Tenga en cuenta que tanto el exponente como la mantisa requieren un bit de señal.

Solución

En punto flotante, el número de bits en el exponente determina los números representables más grandes y más pequeños. Para el punto flotante de 32 bits, los números más grandes (más pequeños) son

\[2^{\pm (127)}=1.7\times 10^{38}(5.9\times 10^{-39}) \nonumber \]

Para el punto flotante de 64 bits, el número más grande es aproximadamente

\[10^{9863} \nonumber \]

Siempre y cuando los enteros no sean demasiado grandes, se pueden representar exactamente en una computadora usando la notación posicional binaria. Los circuitos electrónicos que conforman la computadora física pueden sumar y restar enteros sin error. (Esta afirmación no es del todo cierta; ¿cuándo la adición causa problemas?)

Aritmética y lógica informática

Las tablas binarias de suma y multiplicación son

\[\begin{pmatrix} 0+0=0\\ 0+1=1\\ 1+1=10\\ 1+0=1\\ \\ 0\times 0=0\\ 0\times 1=0\\ 1\times 1=1\\ 1\times 0=0 \end{pmatrix} \nonumber \]

Tenga en cuenta que si se ignoran los carry, la resta ⁷ de dos números binarios de un solo dígito produce el mismo bit que la suma Las computadoras usan valores de alto y bajo voltaje para expresar un bit, y una matriz de tales voltajes expresa números similares a la notación posicional. Los circuitos lógicos realizan operaciones aritméticas.

Ejercicio\(\PageIndex{1}\)

Agregar veinticinco y siete en base 2. Tenga en cuenta los acarreos que podrían ocurrir. ¿Por qué el resultado es “agradable”?

Solución

\[25=110011_{2}\; and\; 7=111_{2} \nonumber \]

Encontramos que

\[110011_{2}+111_{2}=100000_{2}=32 \nonumber \]

Las variables de lógica indican verdad o falsedad. AB, el AND de A y B, representa una afirmación de que tanto A como B deben ser verdaderas para que la afirmación sea cierta. Utiliza este tipo de declaración para indicar a los motores de búsqueda que quieres restringir los hits a los casos en los que ocurren ambos eventos A y B. AUB, el OR de A y B, arroja un valor de verdad si cualquiera es cierto. Tenga en cuenta que si representamos la verdad por un “1" y la falsedad por un “0”, la multiplicación binaria corresponde a AND y la suma (ignorando lleva) a XOR. XOR, el exclusivo u operador, equivale a la unión de AUB y A B. El matemático irlandés George Boole descubrió esta equivalencia a mediados del siglo XIX. Se sentó las bases para lo que ahora llamamos álgebra booleana, que expresa como ecuaciones afirmaciones lógicas. Más importante aún, cualquier computadora que utilice representaciones de base 2 y aritmética también puede evaluar fácilmente las declaraciones lógicas. Este hecho hace que un dispositivo computacional basado en enteros sea mucho más potente de lo que podría ser aparente.

Notas al pie

1. Un ejemplo de cálculo simbólico es ordenar una lista de nombres.
2. Existen sistemas alternativos de representación numérica. Por ejemplo, podríamos usar conteo de figuras de palo o números romanos. Estos eran útiles en la antigüedad, pero muy limitantes cuando se trata de cálculos aritméticos: ¿alguna vez intentaste dividir dos números romanos?
3. Necesitas un poco más para hacer eso.
4. En algunas computadoras, esta normalización se lleva a un extremo: el dígito binario principal no se expresa explícitamente, proporcionando un bit extra para representar la mantisa con un poco más precisión. Esta convención se conoce como la notación de los escondidos.
5. A ver si puede encontrar esta representación.
6. Tenga en cuenta que siempre habrá números que tengan una representación infinita en cualquier sistema posicional elegido. La elección de la base define cuáles hacen y cuáles no. Si estuvieras pensando que los números base 10 resolverían esta inexactitud, ten en cuenta que 1/3=0.333333... tiene una representación infinita en decimal (y binario para el caso), pero tiene representación finita en base 3.
7. Un acarreo significa que un cálculo realizado en una posición dada también afecta a otras posiciones. Aquí, 1+1= 10 es un ejemplo de un cálculo que implica un acarreo.