5.12: Sistemas de Tiempo Discreto en el Dominio del Tiempo
- Page ID
- 85368
- Los sistemas de tiempo discreto permiten procesos matemáticamente especificados como la ecuación de diferencia.
Una señal de tiempo discreto\(s(n)\) se retrasa por\(n_0\) las muestras cuando escribimos\(s(n-n)0)\) con\(n_0>0\). Elegir\(n_0\) ser negativo avanza la señal a lo largo de los enteros. A diferencia de los retardos analógicos, los retardos de tiempo discreto solo pueden ser de valor entero. En el dominio de la frecuencia, el retraso de una señal corresponde a un desplazamiento de fase lineal de la transformada de Fourier de tiempo discreto de la señal:
\[s(n=-n_{0}\leftrightarrow e^{-(i2\pi fn_{0})}S(e^{i2\pi f}) \nonumber \]
Los sistemas lineales discreto-tiempo tienen la propiedad de superposición.
\[S\left ( a_{1}x_{1}(n)+a_{2}x_{2}(n) \right )=a_{1}S\left ( x_{1}(n) \right )+a_{2}S\left ( x_{2}(n) \right ) \nonumber \]
Un sistema de tiempo discreto se denomina invariante de desplazamiento (análogo a los sistemas analógicos invariantes en el tiempo) si el retraso de la entrada retrasa la salida correspondiente. Si
\[S\left ( x(n) \right )=y(n) \nonumber \]
Entonces un sistema de cambio invariante tiene la propiedad
\[S\left ( x(n-n_{0}) \right )=y(n-n_{0}) \nonumber \]
Utilizamos el término invariante de desplazamiento para enfatizar que los retardos solo pueden tener valores enteros en tiempo discreto, mientras que en las señales analógicas, los retardos pueden valorarse arbitrariamente.
Queremos concentrarnos en sistemas que sean tanto lineales como invariantes de cambio. Serán estos los que nos permitan el pleno poder del análisis y las implementaciones en el dominio de la frecuencia. Debido a que no tenemos restricciones físicas para “construir” tales sistemas, solo necesitamos una especificación matemática. En sistemas analógicos, la ecuación diferencial especifica la relación entrada-salida en el dominio del tiempo. La especificación de tiempo discreto correspondiente es la ecuación de diferencia.
\[y(n)=a_{1}y(n-1)+...+a_{p}y(n-p)+b_{0}x(n)+b_{1}x(n-1)+...+b_{q}x(n-q) \nonumber \]
Aquí, la señal de salida\(y(n)\) está relacionada con sus valores pasados
\[y(n-1),l=\left \{ 1,...,p \right \} \nonumber \]
y a los valores actuales y pasados de la señal de entrada\(x(n)\). Las características del sistema están determinadas por las elecciones para el número de coeficientes\(p\)\(q\) y los valores de los coeficientes
\[\left \{ a_{1},...,a_{p} \right \}\; and\; \left \{ b_{0},b_{1},...,b_{q} \right \} \nonumber \]
Hay una asimetría en los coeficientes: ¿dónde está\(a_0\)? Este coeficiente multiplicaría el\(y(n)\) término en la ecuación anterior. Esencialmente hemos dividido la ecuación por ella, lo que no cambia la relación insumo-producto. Hemos creado así la convención que siempre\(a_0\) es una.
A diferencia de las ecuaciones diferenciales, que solo proporcionan una descripción implícita de un sistema (de alguna manera debemos resolver la ecuación diferencial), las ecuaciones de diferencia proporcionan una forma explícita de calcular la salida para cualquier entrada. Simplemente expresamos la ecuación de diferencia mediante un programa que calcula cada salida a partir de los valores de salida anteriores, y las entradas actuales y anteriores.
Las ecuaciones de diferencia generalmente se expresan en software con bucles for. Un programa de MATLAB que computaría los primeros 1000 valores de la salida tiene la forma para n= 1:1000 y (n) = sum (a.*y (n-1: -1:n-p)) + sum (b.*x (n: -1:n-q)); end Surge un detalle importante cuando consideramos hacer funcionar este programa; de hecho, como está escrito tiene (al menos) dos errores. ¿Qué valores de entrada y salida entran en el cálculo de y (1)? Necesitamos valores para y (0), y (-1),... , valores que aún no hemos calculado. Para calcularlos, necesitaríamos más valores previos de la salida, que aún no hemos calculado. Para calcular estos valores, necesitaríamos incluso valores anteriores, ad infinitum. La forma de salir de esta situación es especificar las condiciones iniciales del sistema: debemos proporcionar los p valores de salida que ocurrieron antes de que comenzara la entrada. Estos valores pueden ser arbitrarios, pero la elección sí impacta cómo responde el sistema a una entrada dada. Una elección da lugar a un sistema lineal: Hacer cero las condiciones iniciales. La razón radica en la definición de un sistema lineal: La única manera en que la salida a una suma de señales puede ser la suma de las salidas individuales ocurre cuando las condiciones iniciales en cada caso son cero.
El problema de la condición inicial se resuelve dando sentido a la ecuación de diferencia para las entradas que comienzan en algún índice. No obstante, el programa no funcionará por un error de programación, no conceptual. ¿Qué es? ¿Cómo se puede “arreglar”?
Solución
Los índices pueden ser negativos, y esta condición no está permitida en MATLAB. Para solucionarlo, debemos iniciar las señales más adelante en la matriz.
Consideremos el sencillo sistema teniendo\(p = 1\) y\(q = 0\).
\[y(n)=ay(n-1)+bx(n) \nonumber \]
Para calcular la salida en algún índice, esta ecuación de diferencia dice que necesitamos saber cuál es la salida anterior y (n-1) y cuál es la señal de entrada en ese momento de tiempo. Con más detalle, calculemos la salida de este sistema a una entrada de unidad-muestra:
\[x(n)=\delta (n) \nonumber \]
Debido a que la entrada es cero para los índices negativos, comenzamos tratando de calcular la salida en n = 0.
\[y(0)=ay(-1)+b \nonumber \]
¿Cuál es el valor de y (-1)? Debido a que hemos utilizado una entrada que es cero para todos los índices negativos, es razonable suponer que la salida también es cero. Ciertamente, la ecuación de diferencia no describiría un sistema lineal si la entrada que es cero para todos los tiempos no produjera una salida cero. Con este supuesto, y (-1) = 0, dejando y (0) = b. Para n > 0, la unidad-muestra de entrada es cero, lo que nos deja con la ecuación de diferencia
\[\forall n,n> 0:\left ( y(n)=ay(n-1) \right ) \nonumber \]
Podemos imaginar cómo responde el filtro a esta entrada haciendo una tabla.
\[y(n)=ay(n-1)+b\delta (n) \nonumber \]
| n | x (n) | y (n) |
|---|---|---|
| -1 | 0 | 0 |
| 0 | 1 | b |
| 1 | 0 | ba |
| 2 | 0 | ba 2 |
| : | 0 | : |
| n | 0 | ba n |
Los valores de los coeficientes determinan cómo se comporta la salida. El parámetro b puede ser cualquier valor, y sirve como ganancia. El efecto del parámetro a es más complicado (ver Tabla anterior). Si es igual a cero, la salida simplemente es igual a la entrada multiplicada por la ganancia b. Para todos los valores distintos de cero de a, la salida dura para siempre; se dice que tales sistemas son IIR (I nfinito I mpulse R esponse). La razón de esta terminología es que la muestra unitaria también conocida como el impulso (especialmente en situaciones analógicas), y la respuesta del sistema al “impulso” dura para siempre. Si a es positivo y menor que uno, la salida es un exponencial en decadencia. Cuando a = 1, la salida es un paso de unidad. Si a es negativo y mayor que -1, la salida oscila mientras decae exponencialmente. Cuando a = -1, la salida cambia de signo para siempre, alternando entre b y -b. Efectos más dramáticos cuando |a| > 1; ya sea positivo o negativo, la señal de salida se hace cada vez más grande, creciendo exponencialmente.
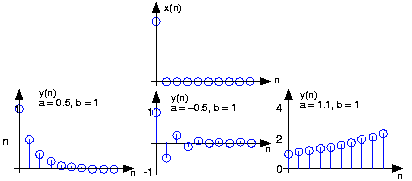
Valores positivos de
Tenga en cuenta que la ecuación de diferencia
\[y(n)=a_{1}y(n-1)+...+a_{p}y(n-p)+b_{0}x(n)+b_{1}x(n-1)+...+b_{q}x(n-q) \nonumber \]
no implica términos como\(y(n+1)\) o\(x(n+1)\) en el lado derecho de la ecuación. ¿Se pueden incluir también tales términos? ¿Por qué o por qué no?
Solución
Dichos términos requerirían que el sistema supiera cuáles serían los futuros valores de entrada o salida antes de que se computara el valor actual. Por lo tanto, tales términos pueden ocasionar dificultades.
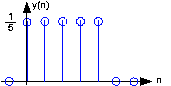
Un sistema algo diferente no tiene coeficientes “a”. Considera la ecuación de diferencia
\[y(n)=\frac{1}{q}\left ( x(n)+...+x(n-q+1) \right ) \nonumber \]
Debido a que la salida de este sistema depende únicamente de los valores de entrada actuales y anteriores, no necesitamos preocuparnos por las condiciones iniciales. Cuando la entrada es una unidad de muestra, la salida es igual
\[\frac{1}{q}\; for\; n=\left \{ 0,...,q-1 \right \} \nonumber \]
entonces equivale a cero a partir de entonces. Se dice que dichos sistemas son FIR (F inite I mpulse R esponse) porque sus respuestas de muestra unitaria tienen duración finita. Al trazar esta respuesta (Figura 5.12.2) se muestra que la respuesta unidad-muestra es un pulso de ancho q y alto 1/q. Esta forma de onda también se conoce como un vagón, de ahí el nombre de filtro de vagón que se le da a este sistema. Derivaremos su respuesta de frecuencia y desarrollaremos su interpretación de filtrado en la siguiente sección. Por ahora, tenga en cuenta que la ecuación de diferencia dice que cada valor de salida es igual al promedio de los valores actuales y anteriores de la entrada. Por lo tanto, la salida es igual al promedio corriente de los valores q anteriores de la entrada. Dicho sistema podría utilizarse para producir la temperatura promedio semanal (q = 7) que podría actualizarse diariamente.
Colaborador
- ContribeeOpenStax


