5.14: Filtrado en el Dominio de Frecuencia
- Page ID
- 85350
- Investigación de diferentes aspectos del filtrado en el dominio de la frecuencia, particularmente el uso de transformadas discretas de Fourier.
Debido a que nos interesan los cálculos reales más que los cálculos analíticos, debemos considerar los detalles de la transformada discreta de Fourier. Para calcular la longitud- N DFT, asumimos que la señal tiene una duración menor o igual a N. Debido a que las respuestas de frecuencia tienen una especificación explícita en el dominio de la frecuencia en términos de coeficientes de filtro, no tenemos un manejador directo en el que la señal tiene una transformada de Fourier igual a una respuesta de frecuencia dada. Encontrar esta señal es bastante fácil. En primer lugar, tenga en cuenta que la transformada de Fourier de tiempo discreto de una muestra unitaria es igual a una para todas las frecuencias. Dado que la entrada y salida de los sistemas lineales, invariantes de desplazamiento están relacionados entre sí por
\[Y\left ( e^{i2\pi f} \right )=H\left ( e^{i2\pi f} \right )X\left ( e^{i2\pi f} \right ) \nonumber \]
Una entrada unidad-muestra, que tiene
\[X\left ( e^{i2\pi f} \right )=1 \nonumber \]
da como resultado que la transformada de Fourier de la salida sea igual a la función de transferencia del sistema.
La afirmación anterior es un resultado muy importante. Derivarlo usted mismo.
Solución
El DTFT de la muestra unitaria equivale a una constante (igual a 1). Así, la transformada de Fourier de la salida es igual a la función de transferencia.
En el dominio del tiempo, la salida para una entrada de muestra unitaria se conoce como respuesta de muestra unitaria del sistema, y se denota por h (n). Combinando las interpretaciones de dominio de frecuencia y dominio de tiempo de la respuesta unidad-muestra de un sistema lineal, invariante de desplazamiento, tenemos que h (n) y la función de transferencia son pares de transformada de Fourier en términos de la transformada de Fourier de tiempo discreto.
\[h(n)\leftrightarrow H\left ( e^{i2\pi f} \right ) \nonumber \]
Volviendo al tema de cómo usar la DFT para realizar el filtrado, podemos especificar analíticamente la respuesta de frecuencia, y derivar la longitud correspondiente- N DFT muestreando la respuesta de frecuencia.
\[\forall k,k=\left \{ 0,...,N-1 \right \}:\left ( H(k)=H\left ( e^{\frac{i2\pi k}{N}}\right ) \right ) \nonumber \]
El cálculo de la DFT inversa produce una señal de longitud N sin importar cuál sea la duración real de la respuesta de muestra unitaria. Si la respuesta unidad-muestra tiene una duración menor o igual a N (es un filtro FIR), calcular la DFT inversa de la respuesta de frecuencia muestreada produce efectivamente la respuesta unidad-muestra. Sin embargo, si la duración excede de N, se encuentran errores. La naturaleza de estos errores se explica fácilmente apelando al Teorema de Muestreo. Por muestreo en el dominio de frecuencia, tenemos el potencial de aliasing en el dominio del tiempo (muestreo en un dominio, ya sea tiempo o frecuencia, puede resultar en aliasing en el otro) a menos que muestremos lo suficientemente rápido. Aquí, la duración de la respuesta unidad-muestra determina la tasa de muestreo mínima que evita el solapamiento. Para los sistemas FIR, por definición, tienen respuestas de muestra unitaria de duración finita, el número de muestras de DFT requeridas es igual a la duración de la respuesta de muestra unitaria:
\[N\geq q \nonumber \]
Derivar la longitud mínima de DFT para una respuesta longitud-q unidad-muestra usando el Teorema de Muestreo. Debido a que el muestreo en el dominio de la frecuencia provoca repeticiones de la respuesta unidad-muestra en el dominio del tiempo, bosquejar el resultado en el dominio del tiempo para varias elecciones de la longitud DFT N.
Solución
Al muestrear una transformada de Fourier de una señal de tiempo discreto L veces por igual sobre [0, 2π) para formar la DFT, la señal correspondiente equivale a la repetición periódica de la señal original.
\[S(k)\leftrightarrow \sum_{i=-\infty }^{\infty }s(n-iL) \nonumber \]
Para evitar el aliasing (en el dominio del tiempo), la longitud de la transformada debe ser igual o superior a la duración de la señal.
Expresar la respuesta unidad-muestra de un filtro FIR en términos de coeficientes de ecuaciones de diferencia. Tenga en cuenta que la pregunta correspondiente para los filtros IIR es mucho más difícil de responder: Consideremos el ejemplo.
Solución
La ecuación de diferencia para un filtro FIR tiene la forma
\[y(n)=\sum_{m=0}^{q}b_{m}x(n-m) \nonumber \]
La respuesta unidad-muestra es igual a
\[h(n)=\sum_{m=0}^{q}b_{m}\delta (n-m) \nonumber \]
que corresponde a la representación descrita en un problema de un filtro de vagón de longitud- q.
Para los sistemas IIR, no podemos usar el DFT para encontrar la respuesta unidad-muestra del sistema: siempre se producirá el aliasing de la respuesta unidad-muestra. En consecuencia, solo podemos implementar un filtro IIR con precisión en el dominio del tiempo con la ecuación de diferencia del sistema. Las implementaciones en el dominio de frecuencia están restringidas a los filtros FIR.
Otro problema surge en el filtrado de dominio de frecuencia que está relacionado con el aliasing de dominio de tiempo, esta vez cuando consideramos la salida. Supongamos que tenemos una señal de entrada que tiene duración N x que pasamos a través de un filtro FIR que tiene una longitud- q+1 unidad-muestra de respuesta. ¿Cuál es la duración de la señal de salida? La ecuación de diferencia para este filtro es
\[y(n)=b_{0}x(n)+...+b_{q}x(n-q) \nonumber \]
Esta ecuación dice que la salida depende de los valores de entrada actuales y pasados, con el valor de entrada q muestras anteriores definiendo la extensión de la memoria del filtro de los valores de entrada pasados. Por ejemplo, la salida en el índice N x depende de x (N x) (que es igual a cero),
\[x(N_{x}-1)\; through\; x(N_{x}-q) \nonumber \]
Así, la salida vuelve a cero solo después de que el último valor de entrada pase a través de la memoria del filtro. Como el último valor de la señal de entrada ocurre en el índice N x - 1, el último valor de salida distinto de cero ocurre cuando
\[n-q=N_{x}-1 \; or\; n=q+N_{x}-1 \nonumber \]
Así, la duración de la señal de salida es igual a q + N x.
En palabras, expresamos este resultado como “La duración de la salida es igual a la duración de la entrada más la duración del filtro menos uno”. Demostrar la exactitud de esta afirmación.
Solución
La duración de la respuesta unidad-muestra es q + 1 y N x de la señal. Así la afirmación es correcta.
El tema principal de este resultado es que la salida de un filtro se extiende más que su entrada o su respuesta unidad-muestra. Así, para evitar el aliasing cuando usamos DFT, el factor dominante no es la duración de la entrada o de la respuesta unidad-muestra, sino de la salida. Así, el número de valores a los que debemos evaluar la DFT de la respuesta de frecuencia debe ser al menos q + N x y debemos calcular la misma longitud DFT de la entrada. Para acomodar una señal más corta que la longitud de DFT, simplemente hacemos una almohadilla cero en la entrada: Asegúrese de que para los índices que se extienden más allá de la duración de la señal, la señal es cero. El filtrado en el dominio de la frecuencia, como se muestra en la Figura 5.14.1 a continuación, se logra almacenando la respuesta de frecuencia del filtro como la DFT H (k), calculando la DFT X (k) de la entrada, multiplicándola para crear la DFT de la salida
\[Y(k)=H(k)X(k) \nonumber \]
y calcular la DFT inversa del resultado para producir y (n).
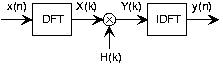
Antes de detallar este procedimiento, aclaremos por qué surgieron tantos problemas nuevos al tratar de desarrollar una implementación de filtrado lineal en el dominio de la frecuencia. La relación frecuencia-dominio entre la entrada y la salida de un filtro es siempre verdadera:
\[Y(e^{i2\pi f})=H(e^{i2\pi f})X(e^{i2\pi f}) \nonumber \]
Las transformadas de Fourier en este resultado son transformadas de Fourier de tiempo discreto; por ejemplo,
\[X(e^{i2\pi f})=\sum_{n}x(n)e^{-(i2\pi fn)} \nonumber \]
Desafortunadamente, el uso de esta relación para realizar el filtrado se restringe a la situación cuando tenemos fórmulas analíticas para la respuesta de frecuencia y la señal de entrada. La razón por la que tuvimos que “inventar” la transformada discreta de Fourier (DFT) tiene el mismo origen: El espectro resultante de la transformada de Fourier de tiempo discreto depende de la variable de frecuencia continua f. Eso está bien para el cálculo analítico, pero computacionalmente tendríamos que hacer un número infinitamente infinito de cálculos.
¿Sabías que se pueden definir de manera significativa dos tipos de infinidades? Una cantidad contablemente infinita significa que se puede asociar con un proceso limitante asociado con números enteros. Una cantidad incontablemente infinita no puede estar tan asociada. El número de números racionales es contablemente infinito (el numerador y el denominador corresponden a ubicar lo racional por fila y columna; el número total así ubicado se puede contar, ¡voila!) ; el número de números irracionales es incontablemente infinito. Adivina cuál es “¿más grande?”
La DFT calcula la transformada de Fourier en un conjunto finito de frecuencias —muestrea el espectro verdadero— lo que puede conducir al aliasing en el dominio del tiempo a menos que muestremos suficientemente rápido. El intervalo de muestreo aquí es 1/K para una longitud- K DFT: un muestreo más rápido para evitar el solapamiento, por lo tanto, requiere un cálculo de transformación más largo. Dado que la señal más larga entre la entrada, la respuesta unidad-muestra y la salida es la salida, es la duración de esa señal la que determina la longitud de la transformación. Simplemente extendemos las otras dos señales con ceros (almohadilla cero) para calcular sus DFT.
Supongamos que queremos promediar los precios diarios de las acciones tomadas el año pasado para producir un promedio semanal corriente (promedio de más de cinco sesiones de negociación). El filtro que queremos es un promedio de longitud-5 (como se muestra en la respuesta unidad-muestra), y la duración de la entrada es 253 (365 días calendario menos días de fin de semana y festivos). La duración de salida será:
\[253+5-1=257 \nonumber \]
Esto determina la longitud de transformación que necesitamos usar. Debido a que queremos usar la FFT, estamos restringidos a longitudes de transformación de potencia de dos. Tenemos que elegir cualquier longitud FFT que exceda la longitud de DFT requerida. Al final resulta que 256 es una potencia de dos
\[2^{8}=256 \nonumber \]
Esta longitud solo disminuye nuestra longitud requerida. Para utilizar técnicas de dominio de frecuencia, debemos usar transformaciones rápidas de Fourier de longitud 512.
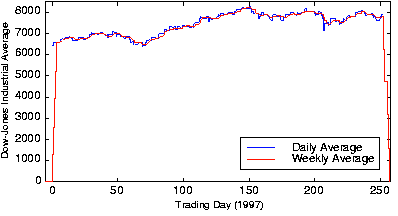
La Figura 5.14.2 anterior, muestra la entrada y la salida filtrada. Los programas MATLAB que calculan la salida filtrada en los dominios de tiempo y frecuencia son:
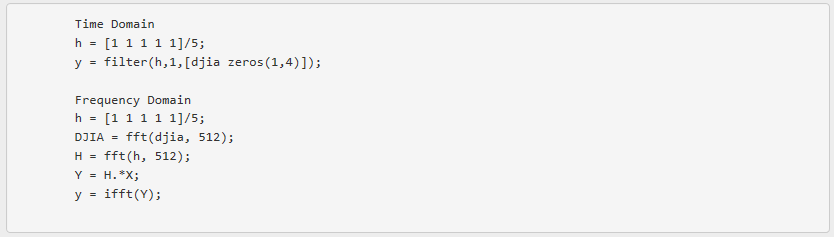
El programa de filtro tiene la característica de que la longitud de su salida es igual a la longitud de su entrada. Para obligarlo a producir una señal que tenga la longitud adecuada, el programa pone a cero la entrada apropiadamente.
La función fft de MATLAB automáticamente pone a cero su entrada si la longitud de transformación especificada (su segundo argumento) excede la longitud de la señal. El resultado del dominio de frecuencia tendrá un pequeño componente imaginario —el valor más grande es 2.2 ×10 -11 — debido a la naturaleza inherente de precisión finita de la aritmética informática. Debido al desafortunado desajuste entre longitudes de señal y longitudes FFT favorecidas, el número de operaciones aritméticas en la implementación en el dominio del tiempo es mucho menor que las requeridas por la versión de dominio de frecuencia: 514 versus 62,271. Si la señal de entrada hubiera sido una muestra más corta, los cálculos en el dominio de la frecuencia habrían sido más de un factor de dos menos (28,696), pero mucho más que en la implementación en el dominio del tiempo.
Un aspecto interesante del procesamiento de señales de este ejemplo se demuestra al principio y al final de la salida. La rampa ascendente y descendente que ocurre se puede rastrear hasta asumir que la entrada es cero antes de que comience y después de que termine. El filtro “ve” estos valores iniciales y finales a medida que la ecuación de diferencia pasa sobre la entrada. Estos artefactos se pueden manejar de dos maneras: podemos simplemente ignorar los efectos de borde o los datos de los años anteriores y siguientes, la semana pasada y la primera semana, respectivamente, se pueden colocar en los extremos.


