3: Propiedades críticas y factor acéntrico
- Page ID
- 82500
Ciencia de la destilación (una mezcla de Química e Ingeniería Química)
Se trata de la Parte III, Propiedades Críticas y Factor Acéntrico de una serie de diez partes de artículos técnicos sobre la Ciencia de la Destilación, como se practica actualmente a nivel industrial. Véase también la Parte I, Panorama general para los comentarios introductorios, los alcances de la serie de artículos y la nomenclatura. El objetivo de este artículo es explicar cómo se utilizan las propiedades críticas y el factor acéntrico, y cómo pueden estimarse cuando no se dispone de valores confiables.
Como se discutió en la Parte II, las ecuaciones de presión de vapor más básicas tienen limitaciones que impiden que sean utilizadas en muchos sistemas modernos de destilación industrial, específicamente a presiones más altas. Los conceptos de este artículo se utilizarán en la Parte IV, para introducir una ecuación de presión de vapor mejorada, que elimina las limitaciones de las ecuaciones básicas de presión de vapor.
Para implementar las relaciones VP más sofisticadas y comparar las constantes en la Parte IV, los datos P vs T medidos experimentalmente deben ser reducidos. Esto se hace sólo con el conocimiento del punto crítico, que es esa singularidad en la línea de saturación donde las fases líquida y vapor se convierten en una sola. La temperatura y presión críticas se identifican como T c y P c. En el punto crítico, el volumen molar específico es V c.
\[T_{r} = T/T_{c} \label{3-1} \]
\(P_{r} = P/P_{c} \nonumber\)
\(V_{r} = V/V_{c} \nonumber\)
(tenga en cuenta que las propiedades reducidas tienen la ventaja de ser adimensionales)
El uso de variables reducidas T r, P r y V r de la Ecuación (\ ref {3-1}) también permite la introducción al concepto de la “Ley de Estados Correspondientes” (que realmente no es una ley científica per se, sino más bien una relación generalmente seguida). Esta “ley” expresa la generalización de que aquellas propiedades dependientes de las fuerzas intermoleculares están relacionadas con las propiedades críticas de la misma manera para todos los fluidos. Este concepto subyace en el desarrollo de varios artículos posteriores de esta serie sobre la Ciencia de la Destilación, entre ellos las Partes IV a VII.
La compresibilidad crítica es Z c, tal como se define como:
\[Z_{c}= \frac {P_{c}V_{c}}{RT_{c}} \label{3-2} \]que también es adimensional.
Otras dos propiedades son importantes a tener en cuenta:
- \(T_b\)se define como el punto de ebullición a presión atmosférica de un fluido, con\(T_{br}\) como el valor reducido del punto de ebullición atmosférico
- \(ω\)es el factor acéntrico, que es una medida de la complejidad molecular tal como se define como:
\[\omega=-\log_{10}(VP)-1 \label{3-3} \]donde el VP (en atmósferas) se evalúa a T r = 0.7
El término “factor acéntrico” proviene de la observación de Kenneth Pfizer en 1955 de que las moléculas compactas y casi esféricas tienen valores cercanos a cero cuando se calcula su ω. Por ejemplo, el neón, el argón y el criptón tienen valores ω de -0.04, 0.00 y 0.00, respectivamente (el helio tiene un ω más ligeramente negativo, el valor depende del isótopo). El metano (CH 4) tiene una ω de 0.011; y el silano molecularmente más grande (SiH 4) tiene una ω de 0.099. Una molécula aún más grande y compleja, como el tetracloruro de carbono (CCl 4) tiene una ω de 0.193; mientras que el tetracloruro de silicio (SiCl 4) tiene una ω de 0.248. Por lo que la valoración del factor acéntrico a partir de los datos VP y el conocimiento del punto crítico es una buena comprobación de validación frente al tamaño molecular y forma conocidos.
Para Ecuaciones de Estado (ver Parte V) que son más avanzadas que Van der Waals, el factor acéntrico es una propiedad requerida, junto con la temperatura y presión críticas. También se utiliza junto con propiedades críticas en la estimación de parámetros de interacción binaria en la Parte VII.
Como se menciona en la Parte II, las relaciones VP básicas tienen una precisión aceptable para obtener buenos valores de T b a partir de los datos disponibles. Los datos experimentales a menudo se toman cerca de la presión atmosférica, pero no exactamente a una atmósfera absoluta (es decir, 760 mmHg = 760 Torr = 101.325 Pa). En lugar de aceptar ciegamente un valor de T b de un manual o sitio web único, el científico o ingeniero en ejercicio debe considerar la fuente y confiabilidad de los datos. Hay disponibilidad inmediata en Internet de puntos de ebullición atmosféricos, datos críticos de propiedades y factores acéntricos, especialmente en el NIST WebBook y sitios web globales como Dechema, Infotherm (recientemente adquirida por John Wiley and Sons de FIZ Chemie Berlin).
Una forma recomendada de clasificar la vertiginosa cantidad de datos críticos de propiedades (es decir, T c, P c y V c) es usar las técnicas de correlación de Lyderson (“Estimation of Critical Properties of Organic Compound”, University of Wisconsin College of Engineering, 1955) y otros, que están específicamente orientados hacia los compuestos orgánicos. Con cierta manipulación algebraica y ajuste de los parámetros de Lyderson (ya que la intención de uso aquí es para compuestos polares que no son orgánicos, pero tampoco iónicos), y en base a datos a través de homólogos, las siguientes relaciones parecen mantenerse y se recomiendan tanto para validar datos cuestionables como rellenando “agujeros” sin datos:
Para T b, la relación de correlación general dentro de un homólogo (por ejemplo, de silano a tetracloruro de silicio, o de fosfina a triclorofosfina):
\[(T_{b}\times MW)^n= A+B\times MW \label{3-4} \]
donde MW es el peso molecular. Para clorosilanos, clorometanos, clorofosfinas, etc, esta relación muestra un mejor ajuste con un exponente “n” de 0.8320. Las constantes A y B para el homólogo son típicamente establecidas por el hidruro y el cloruro, ya que esos datos suelen ser más confiables. Donde el átomo central no es solo carbono o silicio, sino una mezcla (es decir, un metilsilano), un exponente de 0.8455 se ajusta un poco mejor a los datos. Esto contrasta con los compuestos orgánicos, cuyos datos tienden a encajar mejor con exponentes algo menores que se acercan a 0.80.
Para T c (temperatura crítica), se encuentra que la mejor correlación dentro de un homólogo es:
\[\frac {T_{c}-T_{b}}{T_{c}}= A+B\times MW \label{3-5} \]
donde MW es el peso molecular y las constantes A y B para el homólogo son típicamente establecidas por el hidruro y el cloruro, siempre que no haya contenido orgánico y los fluidos sean monoméricos.
Para P c (temperatura crítica), use
\[(\frac {MW}{P_{c}})^n= A+B\times MW \label{3-6} \]
donde MW es el peso molecular, el exponente “n” = 0.5672, y las constantes A y B para el homólogo son típicamente establecidas por el hidruro y el cloruro (siempre que no haya contenido orgánico y los fluidos sean monoméricos). Para un compuesto orgánico puro, el exponente “n” debe ser el 0.5000 sugerido por Lyderson; para los metilsilanos (por ejemplo, dimetil silano) el mejor exponente es 0.4550; y para los compuestos del Grupo III (puentes diméricos unidos) el mejor ajuste de exponente es 1.03-1.08 (1.03 para di-galanos y 1.08 para diboranos).
Para V c (volumen molar crítico), la regla de Lyderson de
\[V_{c}=A+B\times MW \label{3-7} \]
es probablemente el mejor, donde MW es el peso molecular y las constantes A y B para el homólogo son típicamente establecidas por el hidruro y el cloruro. Para algunos homólogos, existe la posibilidad de que la relación Vc vs MW no sea exactamente lineal, sino que tenga una naturaleza cuadrática ligeramente cóncava; pero los datos rara vez son lo suficientemente buenos para determinarlos. De todas las propiedades críticas, V c es la más difícil de medir experimentalmente y se estima frecuentemente.
Hay una manera de sortear parte de la incertidumbre con V c, y es validar (o hacer ajustes menores de V c) con base en el patrón de valores de Z c en el homólogo donde
\[Z_{c}= \frac{P_{c}\times V_{c}}{R\times T_{c}} \label{3-8} \]
Dentro de cada homólogo hay un patrón característico de “marca de control” a los valores de Zc, cuando se grafica contra el número de swaps de hidrógeno a cloro del homólogo (es decir, el hidruro del homólogo tiene cero swaps, el monocloruro un intercambio, el dicloruro dos swaps, etc.). Ver abajo gráfico de datos de ejemplo Figura 3-1 para los homólogos de clorosilano y clorofosfina.
El hidruro del homólogo (que tiende a ser una molécula de forma bastante esférica con un momento dipolar mínimo) típicamente tiene una Z c en el rango de 0.27-0.29. El primer intercambio reemplaza un pequeño átomo “H” con un átomo de “Cl” más grande, y reorienta la forma molecular para tener un dipolo significativo, disminuyendo el valor de Zc en aproximadamente 10%. Entonces los siguientes swaps reducen el dipolo, hasta que la forma molecular vuelve más cerca a la esférica, aunque significativamente mayor en diámetro. Por lo general, la Z c del fluido homólogo completamente clorado tiene una Z c ligeramente mayor que el hidruro del homólogo.
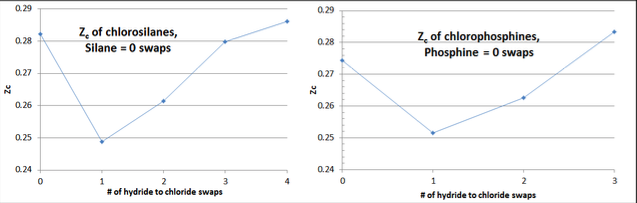
En la medida en que esta forma de “marca de verificación” no se observa en el trazado de valores Z c calculados por la Ecuación 3-8, el “culpable” es casi siempre el valor de V c, lo que permite alguna corrección. Se sabe que el valor de Z c tiene una relación significativa con la forma molecular y la complejidad, aunque la relación más fuerte entre Z c y el factor acéntrico, ω, no se generaliza tan fácilmente como en los compuestos orgánicos.
La importancia de los valores precisos de T b, T c, P c (y ω hasta cierto punto) está en el cálculo de la presión de vapor utilizando la relación avanzada de la Parte IV. Tener un valor exacto de ω es más importante, junto con T c, P c en el cálculo de la Ecuación de Estado para un fluido, en la Parte V. Tener buenos valores para ω y V c son importantes para la estimación de los parámetros de interacción binaria en la Parte VII.
Cuando se realizan dos tipos diferentes de swaps en una molécula ligeramente polar, se utiliza una técnica alternativa para correlacionar mejor las propiedades de los fluidos (T b, T c, P c, V c y ω), siendo un buen ejemplo los metilclorosilanos. Con metilclorosilanos, uno o más grupos metilo se sustituyen por átomos de hidrógeno (es decir, Si-H intercambiado a Si-CH 3), con el enlace Si-H restante posiblemente intercambiado a Si-Cl. Otro ejemplo sería el intercambio de C-H por enlaces C-Cl y C-F en cloro-fluoro metanos. No existe una fórmula concisa que gobierne tal doble sustitución. En cambio se utiliza el concepto de redes neuronales.
En esta técnica, las dos curvas base se presentan a partir del mismo compuesto de partida (silano en el ejemplo siguiente), y en cada curva base se muestran los valores de propiedad física pertinentes para cada homólogo sustituido (clorosilanos y metilsilanos siendo las curvas base en el ejemplo siguiente) vs peso molecular. Por cada cantidad de sustitución combinada (100%, 75% y 50% de sustitución = 0%, 25% y 50% Si-H restante) los puntos de datos están conectados a sus respectivas curvas base. Por ejemplo, en la cantidad de sustitución del 75%, se conectaría por curva triclorosilano, metildiclorosilano, dimetil monoclorosilano y trimetilsilano.
Se podrían hacer conexiones de curva adicionales para valores de cantidad constante de cloro o sustitución de metilo (por ejemplo, monoclorosilano de conexión de curva, metil monoclorosilano, dimetil monoclorosilano y trimetil monoclorosilano). Mediante este método, se pueden validar los datos sobre los fluidos de doble sustitución y realizar ajustes para que las conexiones de la curva sean suaves.
En el ejemplo de abajo Figura 3-2, los valores de P c para metil monoclorosilano (sic, me-mono) y dimetil monoclorosilano (sic, di-me mono) se endurecen a partir de mediciones aproximadas.
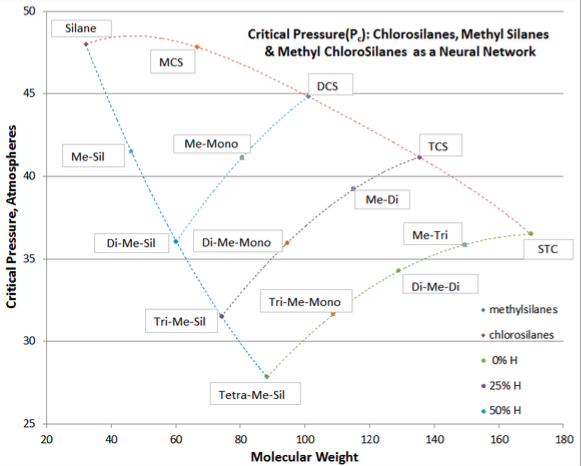
El valor de la técnica de redes neuronales es hacer ajustes donde los datos son pobres o la estimación es de cuestionable precisión. La presunción de las redes neuronales es que para una clase de compuesto, el continuo de cambios estructurales debe ser uniforme e internamente consistente (aunque no necesariamente lineal).
Se construyeron redes neuronales para todas las propiedades pertinentes de los metilclorosilanos, y se encontró que la técnica era bastante simple de tratar gráficamente usando MS Excel. Los valores resultantes se incluyeron en la Tabla 3-3 siguiente, para los clorosilanos y sus impurezas comunes, cuyas propiedades fueron validadas mediante las técnicas de correlación de la Ecuación (\ ref {3-4}) a través de la Ecuación (\ ref {3-8}).
|
Fluido |
MW |
T b |
T c |
P c |
V c |
Z c |
ω |
|---|---|---|---|---|---|---|---|
|
Grupo III (A) |
|||||||
|
B 2 H 6 |
27.670 |
180.54 |
289.70 |
39.58 |
173.10 |
0.2882 |
0.1254 |
|
B 2 H 5 Cl |
62.119 |
216.37 |
346.33 |
37.13 |
189.92 |
0.2481 |
0.1283 |
|
BH 2 Cl como monómero |
42.284 |
237.72 |
379.56 |
37.10 |
206.73 |
0.2463 |
0.1315 |
|
BHCl 2 como monómero |
82.722 |
266.07 |
422.71 |
37.63 |
240.37 |
0.2608 |
0.1389 |
|
B 2 HCl 5 hipotético |
199.893 |
276.67 |
438.47 |
37.92 |
257.18 |
0.2711 |
0.1433 |
|
BCl 3 |
117.169 |
285.88 |
451.95 |
38.20 |
274.00 |
0.2822 |
0.1468 |
|
AlCl 3 como monómero |
133.341 |
466.86 * |
625.70 |
26.00 |
261.80 |
0.1326 |
0.3474 |
|
Ga 2 H 4 Cl 2 como dímero |
214.383 |
350.86 |
545.93 |
40.94 |
231.9 |
0.2120 |
0.2726 |
|
Ga 2 H 2 Cl 4 como dímero |
283.273 |
421.79 |
639.69 |
41.02 |
247.5 |
0.1943 |
0.3525 |
|
Ga 2 Cl 6 como dímero |
352.162 |
473.49 |
694.00 |
37.70 |
263.0 |
0.1741 |
0.4504 |
|
Grupo IV (A) |
|||||||
|
SiH 4 |
32.117 |
161.75 |
269.65 |
47.99 |
130.07 |
0.2821 |
0.09860 |
|
SiH 3 Cl |
66.562 |
242.75 |
396.65 |
47.82 |
169.32 |
0.2488 |
0.1252 |
|
SiH 2 Cl 2 |
101.007 |
281.45 |
449.45 |
44.83 |
215.05 |
0.2614 |
0.1589 |
|
SiHCl 3 |
135.452 |
306.15 |
479.15 |
41.15 |
267.28 |
0.2797 |
0.2090 |
|
SiCl 4 |
169.896 |
330.72 |
506.95 |
36.50 |
326.00 |
0.2860 |
0.2482 |
|
SiH 3 (CH 3) |
46.144 |
216.48 |
348.35 |
41.53 |
185.20 |
0.2691 |
0.1264 |
|
SiH 2 Cl (CH 3) |
80.589 |
278.82 |
439.11 |
41.16 |
233.90 |
0.2672 |
0.1793 |
|
SiHCl 2 (CH 3) |
115.034 |
314.17 |
489.18 |
39.25 |
287.81 |
0.2814 |
0.2269 |
|
SiCl 3 (CH 3) |
149.479 |
339.72 |
517.61 |
35.86 |
345.70 |
0.2919 |
0.2655 |
|
SiH 2 (CH 3) 2 |
60.169 |
252.86 |
399.17 |
36.05 |
245.84 |
0.2706 |
0.1604 |
|
SiHCl (CH 3) 2 |
94.615 |
305.30 |
471.35 |
35.94 |
300.32 |
0.2791 |
0.2264 |
|
SiCl 2 (CH 3) 2 |
129.061 |
342.89 |
519.21 |
34.26 |
358.20 |
0.2880 |
0.2740 |
|
GeH 4 |
76.642 |
184.93 |
307.98 |
54.77 |
128.28 |
0.2780 |
0.1270 |
|
GeH 3 Cl |
111.087 |
302.91 |
495.10 |
49.95 |
180.17 |
0.2215 |
0.1476 |
|
GeH 2 Cl 2 |
145.532 |
334.60 |
536.93 |
45.36 |
236.71 |
0.2437 |
0.1721 |
|
GeHCl 3 |
179.976 |
343.54 |
541.41 |
41.42 |
283.96 |
0.2647 |
0.2012 |
|
GeCL 4 |
214.421 |
357.28 |
553.16 |
38.10 |
335.86 |
0.2819 |
0.2334 |
|
SnH 4 |
122.742 |
221.07 |
360.20 |
51.70 |
152.90 |
0.2674 |
0.1619 |
|
SnCl 4 |
260.521 |
387.21 |
591.85 |
36.95 |
351.20 |
0.2672 |
0.2625 |
|
Grupo V (A) |
|||||||
|
PH 3 |
33.998 |
185.41 |
324.75 |
64.51 |
113.33 |
0.2743 |
0.03052 |
|
PH 2 Cl |
68.443 |
273.09 |
463.73 |
62.29 |
153.63 |
0.2515 |
0.0750 |
|
PhCl 2 |
102.888 |
318.44 |
524.74 |
55.82 |
202.52 |
0.2625 |
0.1362 |
|
PCl 3 |
137.333 |
349.25 |
558.95 |
50.00 |
260.00 |
0.2834 |
0.2117 |
|
POCl 3 |
153.331 |
379.00 |
605.21 |
47.59 |
276.00 |
0.2645 |
0.1993 |
Cuadro 3-3, Continuación
|
aSH 3 |
77.945 |
210.73 |
373.00 |
65.12 |
132.50 |
0.2819 |
0.01341 |
|
Ash 2 Cl |
112.390 |
300.41 |
515.99 |
64.33 |
174.85 |
0.2657 |
0.0573 |
|
AshCl 2 |
146.835 |
359.66 |
600.00 |
61.57 |
218.29 |
0.2730 |
0.1153 |
|
AscL 3 |
181.281 |
403.30 |
654.00 |
58.35 |
259.56 |
0.2822 |
0.1875 |
|
SbH 3 |
124.781 |
256.09 |
446.20 |
66.61 |
157.20 |
0.2860 |
0.01659 |
|
SBCl 3 |
228.115 |
794.05 |
794.05 |
68.85 |
268.00 |
0.2832 |
0.3309 |
|
n-pentano |
72.149 |
309.16 |
470.05 |
32.86 |
310.0 |
0.2641 |
0.2393 |
|
isopentano |
72.149 |
300.82 |
460.56 |
33.17 |
307.1 |
.2695 |
0.2147 |
En el Cuadro 3-3 anterior, aquellas entradas que están marcadas con un tienen su peso molecular dado como el dímero. Para AlCl 3, el asterisco en la entrada T b es para el mejor valor de correlación para la ecuación VP de la Parte IV, aunque esté por debajo del punto triple. “Los compuestos del Grupo IIIA pueden presentar “" enlace puente "” y pueden ser monoméricos o diméricos.” Se incluyen las dos entradas de pentano al final de la tabla por su significación como impurezas electrónicas, y para mostrar que las técnicas pueden extenderse a los orgánicos.
Con el Grupo IIIA, algunos compuestos no se incluyen en un homólogo simplemente porque son imposibles estructuralmente o son inestables. Un ejemplo sería B 2 H 3 Cl 3, lo que pondría demasiada tensión en el enlace puente B-B. Otro es el AlH 3 que no puede existir como un líquido independiente con presión de vapor en condiciones normales de procesamiento, pero tiende a formar hidruros estables con metales del Grupo I como LiAlH 4. Sin embargo, B 2 HCl 5 está incluido (pero señalado como hipotético), ya que algunos investigadores afirman haber visto su presencia en bajos niveles de TCS.


