4: Nueva Ecuación de Presión de Vapor
- Page ID
- 82522
Ciencia de la destilación (una mezcla de Química e Ingeniería Química)
Esta es la Parte IV, Nueva Ecuación de Presión de Vapor de una serie de diez partes de artículos técnicos sobre la Ciencia de la Destilación, como se practica actualmente a nivel industrial. Consulte la Parte I, Sinopsis para comentarios introductorios, el alcance de la serie de artículos y la nomenclatura. Las Partes II y III son prerrequisitos para la Parte IV.
Anterior Parte II, Presión de Vapor trata de las ecuaciones de componentes puros que normalmente se encuentran en los libros de texto, pero que tienen limitaciones en la aplicación industrial. La Parte III, Propiedades Críticas y Factor Acéntrico desarrolla aquellos parámetros utilizados para interrelacionar unidades convencionales de temperatura, presión y volumen con sus equivalentes de propiedades reducidas, así como el factor acéntrico de Pfizer que se utiliza en las Ecuaciones de Estado modernas.
Varias formas de ecuaciones de presión de vapor (VP) termodinámicamente consistentes se han desarrollado en el pasado a propósito para fluidos orgánicos, y típicamente tienen la estipulación de que no funcionan con fluidos polares o fuertemente unidos a hidrógeno. Al ser tanto de naturaleza ligeramente polar como unidos a hidrógeno, los clorosilanos y sus impurezas caen exactamente en esta exclusión, y por lo tanto son buenos ejemplos continuos.
En este artículo, la temperatura y la presión se utilizan en su forma reducida, ya que esto permite una mejor intercomparación entre fluidos, es adimensional y permite un desarrollo futuro más global. La forma reducida se obtiene simplemente dividiendo la temperatura convencional, T, por la temperatura crítica del fluido => T r = T/T c. Del mismo modo, la presión reducida es la presión convencional dividida por la presión crítica del fluido => P r = P/P c. La temperatura y la presión deben estar en unidades absolutas (por ejemplo, ºK no ºC)
Refiriéndose de nuevo a la Parte II, E cuación 2-4, la ecuación de Clausius-Clapeyron se da en formato reducido, utilizando\(\psi \nonumber\) como notación para la derivada termodinámica del logaritmo natural de presión de vapor (reducida) con respecto a la inversa de la temperatura absoluta (reducida):
\[\psi = \frac{-d(\ln P_{r})}{d(1/T_{r})} = \frac{\Delta H_{v}}{\Delta ZRT_{c}} \label{4-1} \]
Para tener una forma de ecuación VP mejorada que pueda ser utilizada para el amplio rango entre T b y T c (es decir, desde la presión atmosférica hasta el punto crítico), esa relación debe cumplir con los siguientes criterios:
- La forma de la ecuación debe tener exactamente un valor VP reducido de 1/P c a T b /T c (es decir, produce el punto de ebullición atmosférico conocido a presión atmosférica), que es un valor de laboratorio bien medido y se estima fácilmente en base a consideraciones estructurales (ver Parte III artículo).
- La forma de la ecuación debe tener exactamente un valor VP reducido de unidad a la temperatura crítica (es decir, coincidir con el valor medido del punto crítico), donde el menisco líquido desaparece. Esta propiedad también se puede estimar fácilmente con base en consideraciones estructurales (ver artículo de la Parte III).
- Dar un valor razonable para VP reducida a T r =0.7, correspondiente a la definición del factor acéntrico de Pfizer, el cual tiene una base en la complejidad molecular (ver artículo de la Parte III).
- Cumplir con las dos pruebas de Reidel de consistencia termodinámica, a medida que se acerca el punto crítico (que “α” cae monótonamente a su valor más bajo en crítico, y que la derivada de temperatura de α = cero en crítico). Consulte la parte más a la izquierda de E quation (\ ref {4-4}) para la definición de “α”.
Tal forma de ecuación VP permitiría evaluar las Ecuaciones de Estado modernas (ver artículo de la Parte V), consideraciones de Fugacidad (ver artículo de la Parte VI) y Parámetros de Interacción Binaria (ver artículo de la Parte VII). Preferiblemente, la forma de la ecuación VP se ajustaría razonablemente a la mayoría de los fluidos (tanto naturales como sintéticos), incluyendo compuestos polares y aquellos con enlaces de hidrógeno sustanciales. Tenga en cuenta que las ecuaciones VP dadas en la Parte II funcionan solo en rangos estrechos; sin embargo, por encima de los criterios #1 y #2 requieren que la forma de la ecuación VP abarque un rango muy amplio. En el texto “Las propiedades de los gases y los líquidos”, de Prausnitz, et al, se discuten varias formas alternas de ecuaciones VP, todas las cuales cumplen con los cuatro criterios anteriores.
En su tesis doctoral en la Universidad de Syracuse en 1965, bajo la dirección de Leonard Stiel, Richard Thek propuso exactamente tal forma de ecuación para llenar el vacío tecnológico. Posteriormente fue publicado por la AIChE en 1966. Desafortunadamente la potencia informática en ese momento era muy limitada, por lo que no se podían utilizar formas de ecuaciones con soluciones iterativas; y la internet no existía para permitir un acceso fácil a los datos globales tomados en las últimas décadas. Utilizando la moderna velocidad de procesamiento informático y programación, estas limitaciones se han resuelto y se han determinado las constantes para todos los clorosilanos y sus impurezas electrónicas.
Según lo dado por la Ecuación (\ ref {4-2}) a continuación, la ecuación original de Thek-Stiel VP en su forma diferencial tiene dos términos: el primero que gobierna a presiones más bajas cercanas a la atmosférica, y el segundo que toma el relevo a medida que se acerca el punto crítico. Mientras que Thek establece variables “q” y “k” iguales a constantes para evitar soluciones iterativas, con la programación moderna estas ahora pueden ser evaluadas como verdaderas variables. La derivación de la ecuación final modificada de Thek-Stiel VP está disponible a pedido, pero no se reproduce en estos artículos por razones de brevedad.
\[\frac{d(\ln P_{r})}{d(1/T_{r})} = \frac{A}{T_{r}^2}[1-B_{1}T_{r}+B_{2}T_{r}^2-B_{3}T_{r}^3+B_{4}T_{r}^4...]+ \frac{c}{T_{r}^2}(T_{r}^n-k) \label{4-2} \]
Las diversas constantes “B” resultan de la expansión binomial de la relación general de Watson para ΔH v. Después de dejar caer los términos de expansión B 4 y superior como matemáticamente no significativos e integrándose, la ecuación de presión de vapor reducida resultante es:
\[ \ln (P_{r})= A[B_{0}-T_{r}^{-1}-B_{1}\ln T_{r}+B_{2}T_{r}-(1/2)B_{3}T_{r}^2]+c\left[\frac{T_{r}^{n-1}-1}{n-1} +k(T_{r}^{-1}-1)\right] \label{4-3} \]
- \(A=\dfrac{\Delta H_{vb}}{RT_{c}(1-T_{br})^q} \nonumber\)
- \(B_{0}=1-B_{2}+(\frac{1}{2})B_{3} \nonumber\)
- \(B_{1}=q \nonumber\)
- \(B_{2}= \dfrac{q(q-1)}{2!} = \dfrac{q(q-1)}{2} \nonumber\)
- \(B_{3}=\dfrac{q(q-1)(q-2)}{3!} = \dfrac{q(q-1)(q-2)}{6} \nonumber\)
- \(c=\dfrac{\alpha_{c} -A(1-B_{1}+B_{2}-B_{3})}{1-k} \nonumber\)
- \(n=(1-k)+\dfrac{A}{c}(1-B_{2}+2B_{3}) \nonumber\)
La valoración de los parámetros de ecuación ΔH vb, q, k y α c se realiza iterativamente utilizando las técnicas de la Parte X, Estrategia de Convergencia, con base en los datos de presión de vapor, la estructura de la molécula y el valor de T br (el punto de ebullición atmosférico reducido, T b /T c = T br). P r debe ser unidad en el punto crítico (T r = 1), lo que permite valorar la constante de integración de la Ecuación 4-3. Las dos importantes funciones derivadas termodinámicas son:
\[\frac{d(\ln P_{r})}{d(\ln T_{r})} = \alpha = A(T_{r}^{-1}-B_{1}+B_{2}T_{r}-B_{3}T_{r}^2)+c(T_{r}^{n-1}-\frac{k}{T_{r}}) \label{4-4} \]
\[\frac{-d(\ln P_{r})}{d(1/T_{r})} = \frac{\Delta H_{v}}{\Delta ZRT_{c}}= \psi = A(1-B_{1}T_{r}+B_{2}T_{r}^2-B_{3}T_{r}^3)+c(T_{r}^n-k) \label{4-5} \]
Las constantes “A” y “B” de las ecuaciones (\ ref {4-2}), (\ ref {4-3}) y (\ ref {4-4}) son las mismas que la Ecuación (\ ref {4-5}). La evaluación de la función derivada de Reidel “α” en la Ecuación (\ ref {4-4}) se utiliza para establecer la consistencia termodinámica, y permite valorar un parámetro de ecuación. Tenga en cuenta que la derivada de Clapeyron de la Ecuación (\ ref {4-5})\(\psi \nonumber\),, es matemáticamente idéntica a la de la Ecuación (\ ref {4-1}). \(\psi \nonumber\)se utilizará la Parte V para establecer el calor latente, ΔH v, así como la densidad de vapor saturado y líquido de los fluidos en las diversas condiciones en el modelado de la columna de destilación.
Utilizando los resultados de la Parte III, las constantes de la Ecuación VP de Thek-Stiel Modificada se dan a continuación en la Tabla 4-1, para clorosilanos e impurezas electrónicas que se encuentran en la fabricación de silicio de alta pureza. Por brevedad, los valores del factor acéntrico, ω, y la derivada crítica de Riedel,\(\alpha_{c} \nonumber \), no se dan en la tabla. Se pueden calcular a partir de las otras constantes de ecuación. En algunos casos, una impureza electrónica puede tener forma monomérica o dimérica, pero la forma se anota en la tabla. Cuando un compuesto no es estable, el lector notará un “agujero” en la tabla (por ejemplo, AlH 3 y Ga 2 H 6 no son estables como líquidos o vapores).
Debido a que la solución a la Ecuación VP de Thek-Stiel Modificada es necesariamente iterativa, la aplicación de esta relación VP requiere el uso de algunas herramientas informáticas modernas para realizar dichos cálculos iterativos (también conocidos como “bucles anidados”). Dependiendo de la preferencia, esto podría hacerse como una macro en un programa de hoja de cálculo como MS Excel, o un programa independiente desarrollado en BASIC (o MatLab o Fortran). Como se mencionó anteriormente, en la Parte X se dan algunos consejos sobre estrategia de convergencia.
La Tabla 4-1 es bastante expansiva, para ilustrar cuán general es la nueva relación VP. La organización de la tabla se realiza principalmente por el Grupo de la Tabla Periódica (por ejemplo, Grupo III, Grupo IV y Grupo V) del átomo central de la molécula, y luego por el homólogo de hidruro a cloruro. Los metilclorosilanos se incluyen como ejemplos de buena aplicación a fluidos que forman el límite entre clásicamente orgánicos e inorgánicos. Se incluyen dos de los pentanos, que resultan ser de interés industrial como impurezas electrónicas, para ilustrar que la nueva ecuación VP también es útil para fluidos orgánicos.
Si bien los fluidos volátiles del Grupo II, Grupo VI y Grupo VII parecen seguir también la nueva relación VP, no hay entradas dadas en la Tabla 4-1 ya que estos fluidos generalmente no son motivo de preocupación en la producción de materiales electrónicos. Se anima al lector a seguir las técnicas de evaluación y estratagemas que se dan en estos artículos para seguir desarrollando el uso de las nuevas ecuaciones VP.
Tabla 4-1, constantes de solución VP, por grupo y homólogo
|
Fluido |
MW |
A |
B 0 |
B 1 |
B 2 |
B 3 |
c |
n |
k |
|
Grupo III (A) |
|||||||||
|
B 2 H 6 |
27.670 |
8.9910 |
1.1494 |
0.37848 |
-0.11762 |
0.063573 |
2.8701 |
4.7796 |
0.1197 |
|
B 2 H 5 Cl |
62.119 |
8.1915 |
1.1494 |
0.37867 |
-0.11764 |
0.063578 |
3.4560 |
3.8431 |
0.1073 |
|
BH 2 Cl como monómero |
42.284 |
8.3872 |
1.1495 |
0.37888 |
-0.11766 |
0.063583 |
3.2767 |
4.0925 |
0.0938 |
|
BHCl 2 como monómero |
82.722 |
8.9910 |
1.1495 |
0.37937 |
-0.11772 |
0.063596 |
2.7577 |
4.9953 |
0.0636 |
|
BCl 3 |
117.169 |
9.5652 |
1.1496 |
0.37988 |
-0.11779 |
0.063609 |
2.2357 |
6.2975 |
0.0291 |
|
AlCl 3 como monómero |
133.341 |
11.9183 |
1.1512 |
0.39300 |
-0.11928 |
0.063892 |
2.2700 |
7.5185 |
0.0291 |
|
Ga 2 H 4 Cl 2 como dímero |
214.383 |
7.0714 |
1.1506 |
0.38810 |
-0.11874 |
0.063799 |
5.3346 |
2.5583 |
0.0938 |
|
Ga 2 H 2 Cl 4 como dímero |
283.273 |
10.8499 |
1.1513 |
0.39333 |
-0.11931 |
0.063898 |
3.3656 |
4.9567 |
0.0636 |
|
Ga 2 Cl 6 como dímero |
352.162 |
11.1760 |
1.1520 |
0.39974 |
0.11997 |
0.063996 |
3.8566 |
4.5874 |
0.0291 |
|
Grupo IV (A) |
|||||||||
|
SiH 4 |
32.117 |
7.4652 |
1.1492 |
0.37673 |
-0.11740 |
0.063525 |
3.6247 |
3.4716 |
0.0914 |
|
SiH 3 Cl |
66.562 |
8.8830 |
1.1494 |
0.37847 |
-0.11761 |
0.063572 |
2.7614 |
4.9286 |
0.0756 |
|
SiH 2 Cl 2 |
101.007 |
9.9221 |
1.1497 |
0.38068 |
-0.11788 |
0.063629 |
2.1589 |
6.6627 |
0.0598 |
|
SiHCl 3 |
135.452 |
9.9796 |
1.1501 |
0.38395 |
-0.11827 |
0.063708 |
2.5687 |
5.7950 |
0.0446 |
|
SiCl 4 |
169.896 |
10.0240 |
1.1504 |
0.38651 |
-0.11856 |
0.063765 |
2.8465 |
5.3590 |
0.0291 |
|
SiH 3 (CH 3) |
46.144 |
9.0535 |
1.1494 |
0.37855 |
-0.11762 |
0.063574 |
2.6380 |
5.1963 |
0.0758 |
|
SiH 2 Cl (CH 3) |
80.589 |
10.1402 |
1.1499 |
0.38201 |
-0.11804 |
0.063662 |
2.1796 |
6.7338 |
0.0600 |
|
SiHCl 2 (CH 3) |
115.034 |
9.1805 |
1.1503 |
0.38512 |
-0.11840 |
0.063735 |
3.3346 |
4.3854 |
0.0446 |
|
SiCl 3 (CH 3) |
149.479 |
10.1187 |
1.1506 |
0.38512 |
-0.11840 |
0.063789 |
2.9357 |
5.2665 |
0.0291 |
|
SiH 2 (CH 3) 2 |
60.169 |
8.2747 |
1.1497 |
0.38077 |
-0.11789 |
0.063631 |
3.4554 |
3.9214 |
0.0603 |
|
SiHCl (CH 3) 2 |
94.615 |
9.1914 |
1.1503 |
0.38509 |
-0.11840 |
0.063734 |
3.3232 |
4.4012 |
0.0447 |
|
SiCl 2 (CH 3) 2 |
129.061 |
10.1007 |
1.1507 |
0.38820 |
-0.11875 |
0.063801 |
3.0279 |
5.1285 |
0.0291 |
|
GeH 4 |
76.642 |
8.1986 |
1.1494 |
0.37858 |
-0.11763 |
0.063575 |
3.3615 |
3.9445 |
0.0914 |
|
GeH 3 Cl |
111.087 |
8.6130 |
1.1496 |
0.37993 |
-0.11779 |
0.063610 |
3.1743 |
4.3025 |
0.0756 |
|
GeH 2 Cl 2 |
145.532 |
8.8966 |
1.1498 |
0.38154 |
-0.11798 |
0.063650 |
3.1184 |
4.4929 |
0.0598 |
|
GeHCl 3 |
179.976 |
9.1230 |
1.1501 |
0.38344 |
-0.11821 |
0.063696 |
3.1490 |
4.5641 |
0.0446 |
|
GeCL 4 |
214.421 |
9.4041 |
1.1503 |
0.38554 |
-0.11845 |
0.063744 |
3.1654 |
4.6724 |
0.0291 |
|
SnH 4 |
122.742 |
9.0298 |
1.1497 |
0.38087 |
-0.11790 |
0.063634 |
3.0671 |
4.5745 |
0.0914 |
|
SnCl 4 |
260.521 |
10.1994 |
1.1506 |
0.38745 |
-0.11867 |
0.063744 |
2.8471 |
5.4354 |
0.0291 |
|
Grupo V (A) |
|||||||||
|
PH 3 |
33.998 |
7.8041 |
1.1485 |
0.37228 |
-0.11684 |
0.063396 |
2.8050 |
4.3644 |
0.1009 |
|
PH 2 Cl |
68.443 |
8.6412 |
1.1490 |
0.37518 |
-0.11721 |
0.063482 |
2.4920 |
5.2267 |
0.0766 |
|
PhCl 2 |
102.888 |
8.5412 |
1.1495 |
0.37919 |
-0.11770 |
0.063591 |
3.0719 |
4.3813 |
0.0527 |
|
PCl 3 |
137.333 |
7.2366 |
1.1501 |
0.38413 |
-0.11829 |
0.063712 |
4.4289 |
2.9789 |
0.0291 |
|
POCl 3 |
153.331 |
9.7746 |
1.1500 |
0.38331 |
-0.11819 |
0.063693 |
2.4586 |
5.9576 |
0 |
Cuadro 4-2, Soluciones VP, por Grupo y Homólogo, continuación
|
Fluido |
MW |
A |
B 0 |
B 1 |
B 2 |
B 3 |
c |
n |
k |
|
Grupo V (A), cont. |
|||||||||
|
Ash 3 |
77.945 |
7.4208 |
1.1484 |
0.37116 |
-0.11670 |
0.063362 |
2.9474 |
4.0298 |
0.1009 |
|
Ash 2 Cl |
112.390 |
8.5242 |
1.1488 |
0.37403 |
-0.11707 |
0.063448 |
2.3972 |
5.3468 |
0.0766 |
|
AshCl 2 |
146.835 |
9.3548 |
1.1493 |
0.37782 |
-0.11754 |
0.063555 |
2.1821 |
6.2831 |
0.0527 |
|
AscL 3 |
181.281 |
10.0281 |
1.1499 |
0.38254 |
-0.11810 |
0.063675 |
2.2519 |
6.5171 |
0.0291 |
|
SbH 3 |
124.781 |
8.5409 |
1.1484 |
0.37136 |
-0.11673 |
0.063368 |
2.0491 |
6.0821 |
0.1009 |
|
SBCl 3 |
228.115 |
7.1200 |
1.1511 |
0.39192 |
-0.11916 |
0.063873 |
5.3455 |
2.6317 |
0.0291 |
|
n-pentano |
72.149 |
10.0508 |
1.1504 |
0.38593 |
-0.11849 |
0.063753 |
2.6269 |
5.7673 |
0 |
|
isopentano |
72.149 |
9.9797 |
1.1502 |
0.38432 |
-0.11831 |
0.063717 |
2.4514 |
6.0715 |
0 |
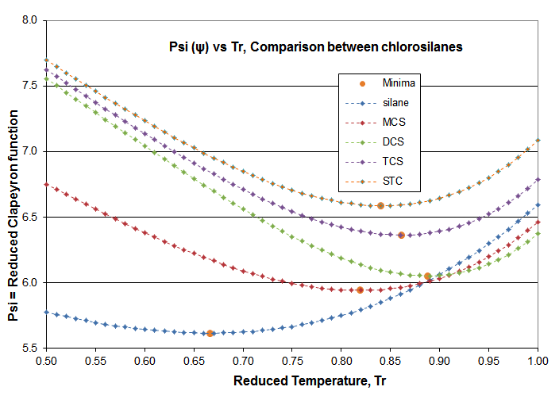
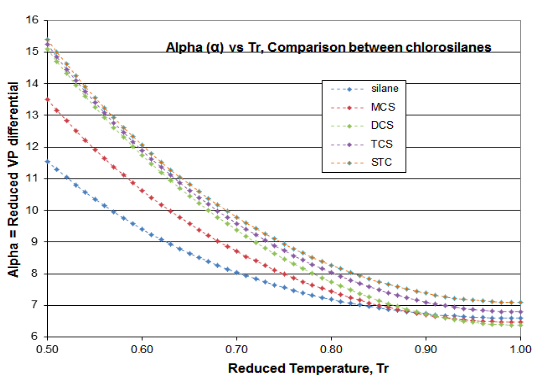
Se ofrecen dos parcelas en la Figura 4-3 para validar los principios de este artículo de Ciencia de la Destilación. Estas gráficas son para la función\(\psi \) (Psi) de la Ecuación (\ ref {4-5}) y la función\(\alpha \) (alfa) de la Ecuación (\ ref {4-4}), para el homólogo de cloroilano. La función derivada\(\phi \) pasa por el mínimo requerido, lo que produce la inflexión esperada en la curva de presión de vapor, típicamente alrededor de T r = 0.80-0.86. El mínimo de silano\(\phi \) ocurre a T r =0.67 y el mínimo de DCS\(\phi \) ocurre a T r = 0.89. El hecho de que dos fluidos de este homólogo sean valores atípicos ilustra por qué las presiones de vapor de clorosilano están tan mal ajustadas por las expresiones VP que están destinadas a su uso con hidrocarburos. Sin embargo, se puede ver cómo la\(\alpha \) función Reidel sí se ajusta a los requisitos de consistencia termodinámica: para todos los fluidos homólogos, la\(\alpha \) función asíntota a un valor constante (\(\alpha_{c} \)) como punto crítico se aproxima, con la pendiente de la\(\alpha \) función yendo a cero como crítico es abordado.
Otra comprobación de validación se muestra en la Figura 4-4, comparando las presiones de vapor de clorosilanos y clorofosfinas, las cuales son aplicaciones de separación por destilación en toda la purificación comercial de clorosilanos.
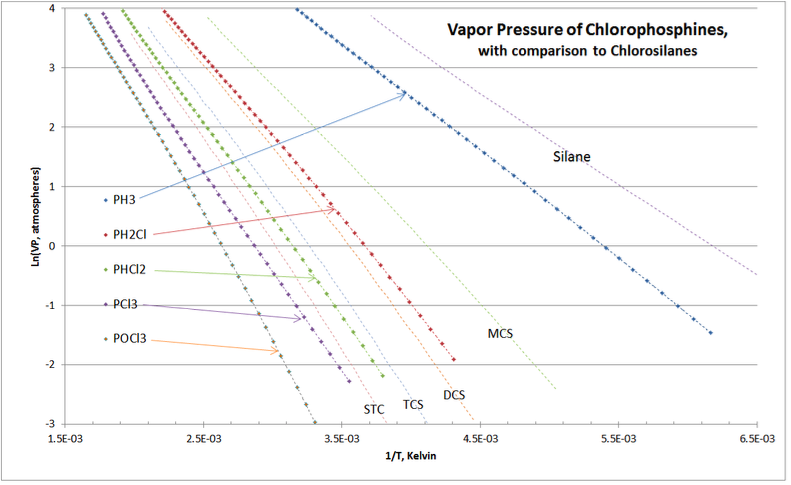
Como era de esperar, las curvas VP del homólogo de clorofosfina “anidan” alrededor de las de los clorosilanos. No hay cruces de las curvas, y la ubicación de las curvas de presión de vapor de clorofosfina se encuentran exactamente como se experimentan en la práctica comercial de columnas de destilación de purificación de clorosilanos.
Dado que la matemática en la ecuación (\ ref {4-3}) está algo involucrada, se proporciona un ejemplo con cálculos.
Ejemplo: A una presión de 3.50 atmósferas ¿cuál es el punto de ebullición del triclorosilano (TCS)?
De la Parte III, Cuadro 3-3, los valores de propiedad pertinentes para TCS son: T c =479.15°K y P c =41.15 atm. MW, T b, V c y Z c no son necesarios para este ejemplo. De la Parte IV, las constantes de solución VP para TCS son: A=9.9796; B 0 =1.1501; B 1 =0.38395; B 2 =-0.11827; B 3 =0.063708; c=2.5687; n=5.7950; y k=0.0446.
Como son todas las ecuaciones VP avanzadas, determinar el punto de ebullición TCS en 3.50 atmósferas es iterativo; así que es bueno tener una gráfica VP para obtener una buena primera suposición. Usando la Figura 4‑4 anterior, para
\ ln (VP) =\ ln (3.50) = 1.2528, parece que 1/T= 2.89E-3 podría ser una buena primera suposición => T=346°K; así que primero adivina T r =346/479.15 =0.7221. Conectando ese primer valor de conjetura de T r a la ecuación T-S VP con las constantes anteriores:
\( \ln (P_{r})= A[B_{0}-T_{r}^{-1}-B_{1}\ln T_{r}+B_{2}T_{r}-(1/2)B_{3}T_{r}^2]+c[\frac{T_{r}^{n-1}-1}{n-1} +k(T_{r}^{-1}-1)] \nonumber\)produce un valor VP reducido de P r = 0.08273; así VP=0.08273*41.15 = 3.404 atm, que es apenas un poco menor que los 3.50 atm deseados. Entonces T necesita aumentar un poco desde la primera suposición inicial de 346°K.
Rehacer la ecuación TCS VP con T= 347°K produce un VP de 3.50 atm (nota: 347.05°K es la respuesta, si la solución se elabora a dos decimales de temperatura). Por lo que la temperatura de ebullición a 3.50 atmósferas es de 347°K o 73.9°C.


