4.5: El perfil espacial del potencial

Como se muestra en la Figura\(\PageIndex{1}\), a continuación, el alambre puede describirse por su relación de dispersión o por su densidad de estados (DOS). La relación de dispersión describe una banda de estados conductores. La parte inferior de la banda se conoce como el borde de la banda de conducción. Corresponde a la energía más baja para un estado de onda plana en el cable. El borde de la banda de conducción es particularmente importante porque su posición controla el flujo de corriente en el cable. Si está por debajo de la función de trabajo fuente, entonces los electrones se inyectan fácilmente en el cable. Por el contrario, si el borde de la banda de conducción está por encima de la función de trabajo fuente, entonces el flujo de corriente requiere electrones con energía térmica adicional.

Figura\(\PageIndex{1}\): Dos representaciones de un cable cuántico 1-d. La relación de dispersión a la izquierda muestra una banda de energías disponibles para la conducción. La densidad de estados a la derecha cae a cero por debajo del borde de la banda de conducción (\(E_{C}\)).

Figura\(\PageIndex{2}\): La posición del borde de la banda de conducción\(E_{C}\),, determina si la carga puede ser inyectada desde la fuente al alambre.

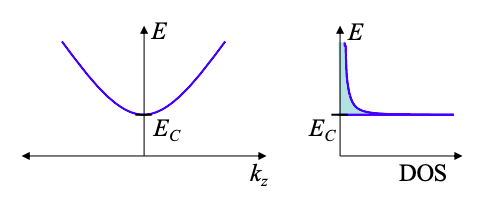
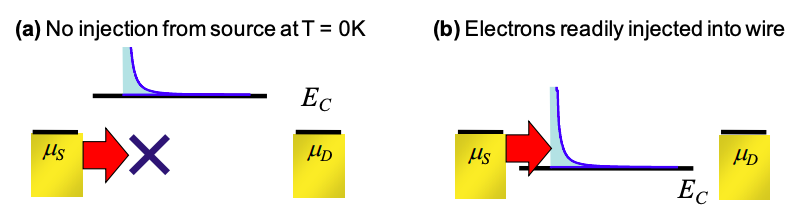
La aplicación de una polarización puede posteriormente la posición del borde de la banda de conducción cambiando el potencial electrostático local, U. Dos ejemplos se muestran en la Figura 4.5.3, a continuación.

Figura\(\PageIndex{3}\): (a) Un alambre metálico bajo polarización. (b) Un cable aislante o nanoescala bajo polarización. Tenga en cuenta que el borde de la banda de conducción corresponde al potencial máximo en el cable. Esto se explica en (c), donde consideramos las funciones de onda electrónicas en el cable bajo polarización. Hemos aplicado condiciones de límite periódicas para ayudar a demostrar que los estados electrónicos con energías por debajo del potencial máximo están localizados. A estos estados sólo se puede acceder mediante tunelización desde la fuente. Los estados electrónicos por encima del potencial máximo son ondas planas deslocalizadas. En consecuencia, el borde de la banda de conducción se posiciona en el punto del máximo potencial repulsivo en el cable.

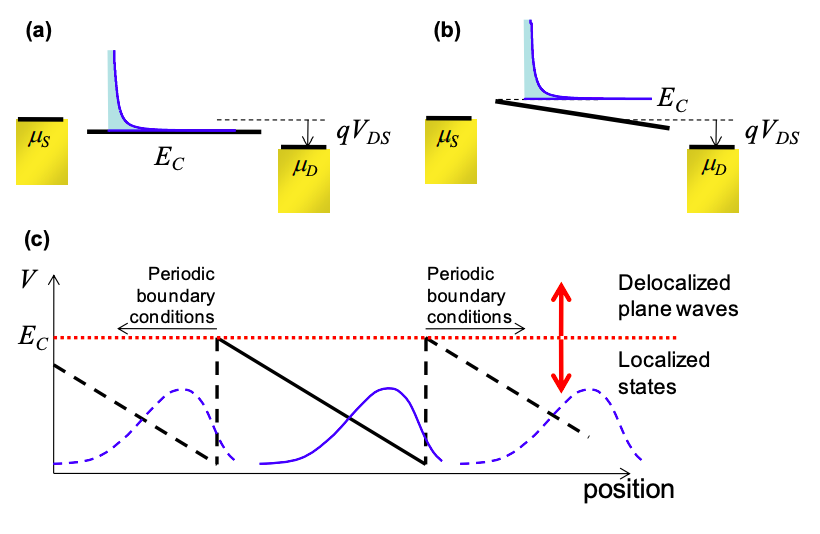
El primer ejemplo de la Figura 4.5.3 demuestra un alambre metálico bajo polarización. En este límite no hay variación potencial a lo largo del cable. En (b) de la Figura 4.5.3 presentamos un cable con potencial variable a lo largo de su longitud. El borde de la banda de conducción\(E_{C}\),, ocurre en el punto de máximo potencial repulsivo. Esto se explica en (c) de la Figura 4.5.3. Las funciones de onda electrónicas en el cable con energías por debajo\(E_{C}\) se localizan y solo se puede acceder desde la fuente mediante tunelización a través de un potencial repulsivo. Debido a la tasa relativamente baja de inyección en estos estados ignoraremos la corriente a través de estos modos en esta clase. Por encima\(E_{C}\), sin embargo, las funciones de onda de electrones son ondas planas deslocalizadas que transportan fácilmente electrones entre los contactos.

Determinar el perfil potencial del cable puede ser Considere un punto, z, en el cable. El potencial electrostático en el punto z viene dado por

\[ U(z) = -qV_{DS} \frac{C_{D}(z)}{C_{ES}(z)} \nonumber \]

donde\(C_{D}\) es la capacitancia que une el punto en z al drenaje, y\(C_{S}\) es la capacitancia que une el punto en z a la fuente, y\(C_{ES}(z)\) es la capacitancia electrostática total en z;\(C_{ES}(z)=C_{S}(z)+C_{D}(z)\).

Si asumimos que las capacitancias de fuente y drenaje pueden modelarse mediante condensadores de placa paralela, encontramos en la Ecuación (3.5.5) que el potencial varía linealmente entre los contactos. Sin embargo, la carga del conductor puede cambiar el perfil de potencial al oponerse a los cambios inducidos por la tensión de la fuente de drenaje. Al agregar el efecto de la carga a la Ecuación (4.5.1) se obtiene:

\[ U = -qV_{DS}\frac{C_{D}}{C_{ES}}+\frac{q^{2}(N-N_{0})}{C_{ES}} \nonumber \]

Recuerde que todas estas capacitancias electrostáticas varían con la posición a lo largo del cable. A continuación, supongamos que el sesgo aplicado es pequeño y en consecuencia el cambio de carga es pequeño i.e\(\delta N = N-N_{0}\). Podemos\(\delta N\) relacionarnos con la densidad de estados a nivel Fermi en el alambre\(g(E_{F})\), y el cambio de potencial,\(\delta U\).

\[ \delta U = -q\delta V_{DS}\frac{C_{D}}{C_{ES}}-\frac{q^{2}g(E_{F})}{C_{ES}}\delta U \nonumber \]

Sustituir la capacitancia cuántica\(C_{Q} = q^{2}g(E_{F})\) y los términos de recolección da

\[ \delta U=-q\delta V_{DS} \frac{C_{D}}{C_{ES}+C_{Q}} \nonumber \]

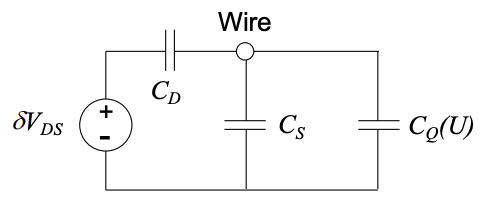
El circuito equivalente se muestra en la Figura 4.5.4. Tenga en cuenta que la capacitancia cuántica depende de la posición del nivel Fermi dentro del DOS. Debido a que el potencial desplaza el DOS en relación con el nivel de Fermi, la capacitancia cuántica también depende del potencial.

En esta clase consideraremos dos casos extremos:\(C_{Q}\ggC_{ES}\) y\(C_{Q}\llC_{ES}\). El primer caso corresponde a un alambre perfectamente metálico. El último caso puede corresponder ya sea a un aislante perfecto o a un conductor a nanoescala, que por su tamaño, tiene muy pocos estados electrónicos.

Figura\(\PageIndex{4}\): El circuito equivalente para determinar el potencial en un nanocables bajo polarización. Cuando la capacitancia cuántica,\(C_{Q}\), es grande, el potencial en el cable varía poco con el sesgo aplicado. Esto corresponde al comportamiento de un alambre metálico. En aisladores o cables más pequeños con menos estados electrónicos, el potencial varía con la posición en el cable.

Alambres perfectamente metálicos

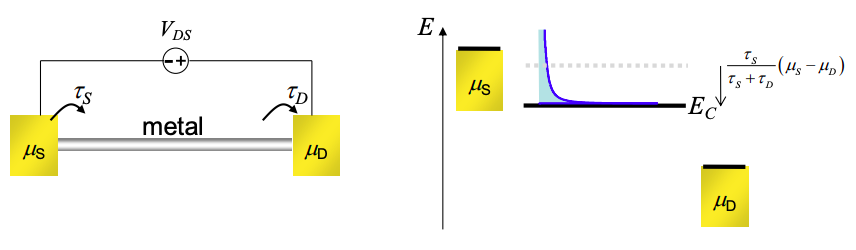
En el límite que\(C_{Q}\ggC_{ES}\), la Ecuación (4.5.4) se reduce a\(\delta U = 0\), lo que significa que el potencial se fija a lo largo de la longitud del alambre por la gran densidad de estados en el Nivel Fermi. El potencial del cable con respecto a los contactos se determina entonces por las propiedades de contacto, en particular los coeficientes de acoplamiento\(\tau_{S}\) y\(\tau_{D}\). El potencial se determina a partir del análisis de la Figura 3.9.1.

Figura\(\PageIndex{5}\): El potencial de un alambre metálico es constante a lo largo de su longitud. La posición del borde de la banda de conducción puede modelarse mediante un divisor de voltaje donde los coeficientes de acoplamiento de fuente y drenaje\(\tau_{S}\) y\(\tau_{D}\), respectivamente, representan las resistencias de contacto de fuente y drenaje.

El límite de aislador/nanoescala

El espaciamiento entre k estados en un conductor 1-d es simplemente\(\Delta k = 2\pi/L\), donde L es la longitud del cable. Cuando L es pequeño hay pocos estados disponibles para los electrones. En consecuencia, los aisladores y muchos conductores muy pequeños tienen relativamente pocos estados para los electrones a nivel Fermi. Podemos ignorar los efectos de carga en estos conductores. El potencial es entonces simplemente descrito por la Ecuación (4.5.1).