4.9: Ley de Ohm
- Page ID
- 84522
¿Qué sucede cuando aumentamos el tamaño de un conductor? Finalmente, deberíamos obtener la ley de Ohm a medida que los fenómenos cuánticos se transforman en el modelo familiar de conducción clásica:
\[ V=IR \nonumber \]
Pero una relación lineal entre V e I no es particularmente profunda. Casi cualquier sistema se puede linealizar en un rango suficientemente estrecho de voltaje o corriente. Es más significativo evaluar la resistencia, R, en términos de cantidades macroscópicas como área transversal, A, y longitud, L.
Tal vez recuerdes que la resistencia se define clásicamente como:
\[ R = \frac{\rho L}{A} . \nonumber \]
donde\(\rho\), la resistividad, es alguna cantidad dependiente del material, generalmente determinada por una medición. Veamos de dónde viene esta expresión — ayudará a ilustrar las diferencias entre los modelos cuánticos y clásicos de conducción de carga.
A temperatura cero, el formalismo de transmisión da
\[ G = \frac{2q^{2}}{h} M \Im \nonumber \]
donde M es el número de modos, y\(\Im\) es el coeficiente de transmisión neto. Reordenando esto en términos de resistencia, tenemos
\[ R = \frac{h}{2q^{2}} \frac{1}{M \Im} \nonumber \]
Para determinar el coeficiente de transmisión neto, vamos a romper el conductor en una serie de N elementos etiquetados\(i = 1… N\), cada uno conteniendo un sitio de dispersión con transmisión\(\Im_{i}\); ver Figura 4.9.1.
Para muchos scatterers habrá muchas reflexiones a considerar. Si el mecanismo de dispersión conserva la información de fase de los electrones, entonces múltiples reflexiones pueden producir efectos de interferencia. Se dice que tal dispersión es coherente. Aquí, consideraremos solo la dispersión incoherente que aleatoriza la fase electrónica.
Comencemos con solo dos dispersores incoherentes en serie. La transmisión para dos dispersores incoherentes en serie es:
\[ \Im_{12} = \Im_{1}\Im_{2}+ \Im_{1}\Im_{2}\Re_{1}\Re_{2}+\Im_{1}\Im_{2}(\Re_{1}\Re_{2})^{2} + … \nonumber \]
donde\(\Re_{i}\) esta el reflejo del i th dispersor, y\(\Im_{i}=(1-\Re_{i})\).
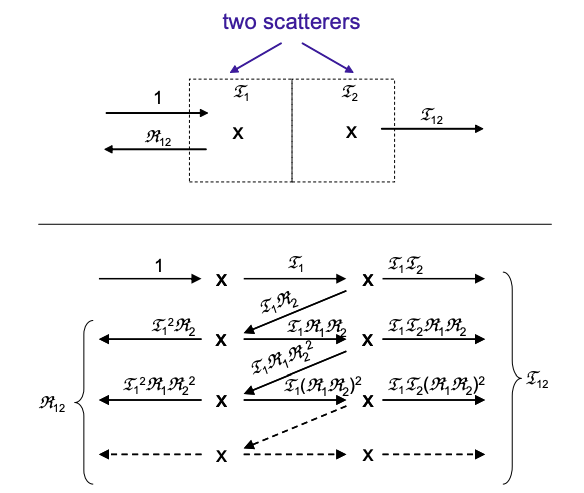
Esta serie geométrica simplifica
\[ \Im_{12}= \frac{\Im_{1}\Im_{2}}{1-\Re_{1}\Re_{2}} , \nonumber \]
Podemos reorganizar la Eq. (4.9.6) para mostrar
\[ \frac{\Re_{12}}{\Im_{12}} = \frac{\Re_{1}}{\Im_{1}} + \frac{\Re_{2}}{\Im_{2}} \nonumber \]
Así, para N dispersores idénticos:
\[ \frac{\Re}{\Im} = N\frac{\Re_{i}}{\Im_{i}} \nonumber \]
Resolviendo para la transmisión neta y el uso\(\Im=(1-\Re)\)
\[ \Im=\frac{\Im_{i}}{N(1-\Im_{i})+\Im_{i}} \nonumber \]
Si tenemos\(\lambda\) dispersores por unidad de longitud, entonces
\[ \tau=\frac{\tau_{i}}{\lambda L(1-\Im_{i})+\Im_{i}}=\frac{L_{0}}{L+L_{0}} \nonumber \]
Así, la Ecuación (4.9.4) se convierte
\[ R = \frac{h}{2q^{2}} \frac{1}{M}\left(1+\frac{L}{L_{0}}\right) \nonumber \]
donde\(L_{0} = \Im/\lambda (1-\Im)\) es una longitud característica. La dependencia de longitud de la resistencia es clara a partir de la Ecuación (4.9.11). La dependencia del área de sección transversal se debe al número de modos de transporte de corriente en el conductor
\[ M \approx \frac{k_{F}^{2}}{4\pi}A , \nonumber \]
donde\(k_{F}\) está el evector de ondas Fermi.
Así, encontramos que la resistencia se puede romper en dos componentes, una resistencia por los contactos, y una resistencia que escala con la longitud del conductor.
\[ R=R_{C}+R_{B}=\frac{\rho L_{0}}{A}+\frac{\rho L}{A} \nonumber \]
La resistencia de contacto es el efecto cuántico que nos resulta familiar a partir de la teoría de Landauer. Pero en conductores grandes, la resistencia de contacto está abrumada y obtenemos la expresión clásica familiar para la resistencia.
\(^{†}\)Esta sección está adaptada de S. Datta, “Transporte electrónico en sistemas mesoscópicos” Cambridge (1995).


