5.13: FET de pozo cuántico balístico
- Page ID
- 84192
Para analizar el FET de pozo cuántico balístico, comencemos con la ecuación maestra para corriente.
\[ I = \frac{q(N_{S}-N_{D})}{\tau} = \frac{q(N_{S}-N_{D})v_{x}}{L} \nonumber \]
Hemos definido la conducción en la dirección x y el tiempo de tránsito viene dado por\(\tau = L_{x}/v_{x}\).
Empecemos por considerar el producto\(g.v_{x}\), que integraremos para obtener\((N_{S} - N_{D})v_{x}\). En k -espacio y coordenadas circulares, esto es
\[ g(k)v_{x}(k)kdkd\theta=2\frac{1}{(2\pi)^{2}/LW}\frac{\hbar k_{x}}{m}kdkd\theta \nonumber \]
Simplificar aún más da:
\[ g(k)v_{x}(k)kdkd\theta=\frac{LW}{(2\pi)^{2}}\frac{\hbar}{m}k^{2}dk \text{ sin}\theta d\theta \nonumber \]
Convertir la variable de integración de nuevo a energía usando la relación de dispersión\(E = \hbar^{2}k^{2}/2m + E_{C}+U\), y asumiendo la conducción en un solo modo del pozo cuántico, rinde
\[ g(k)v_{x}(k)kdkd\theta=\frac{LW}{2\pi^{2}\hbar^{2}} \sqrt{2m(E-E_{C}-U)}u(E-E_{C}-U)dE \text{ sin}\theta d\theta \nonumber \]
Sustituyendo de nuevo a la Ecuación (5.13.1) e integrando sobre el hemisferio +k\((0<\theta <\pi)\) da
\[ I= \frac{qW}{\pi^{2}\hbar^{2}}\int^{\infty}_{-\infty} \sqrt{2m(E-E_{C}-U)}u(E-E_{C}-U)(f(E,\mu_{S})-f(E,\mu_{D}))dE \nonumber \]
Por debajo del umbral la densidad de estados es cero. Por lo tanto,
\[ U=-q \eta^{0}V_{GS} \nonumber \]
donde descuidamos el efecto de\(V_{DS}\), y
\( \eta^{0} =\frac{C_{G}}{C_{S}+C_{D}+C_{G}} \)
El voltaje umbral,\(V_{T}\), se define como el voltaje puerta-fuente requerido para encender el transistor, es decir, llevar la parte inferior de la banda de conducción\(E_{C}\),, a la función de trabajo fuente. De la Ecuación (5.13.6) y requiriendo el umbral\(E_{C}+U=\mu_{S}\) at, obtenemos
\[ V_{T} = (E_{C}-\mu_{S})/\eta^{0}q \nonumber \]
Por encima del umbral la densidad de estados y por lo tanto la capacitancia cuántica es constante. Así, el FET de pozo cuántico es el raro caso en el que podemos modelar los fenómenos de carga analíticamente. Por encima del umbral tenemos
\[ U = -\eta q(V_{GS}-V_{T})-\eta^{0}qV_{T} \nonumber \]
donde nuevamente descuidamos el efecto de\(V_{DS}\), y
\[ \eta=\frac{C_{G}}{C_{S}+C_{D}+C_{G}+C_{Q}} \nonumber \]
A partir del DOS 2-d en la Ecuación (2.12.4),\(C_{Q}\) para un pozo cuántico de modo único es
\[ C_{Q} = \frac{1}{2}q^{2}\frac{mWL}{\pi \hbar^{2}} . \nonumber \]
donde solo hemos considerado la mitad de la densidad habitual de estados (los estados +k). Esto es exacto en la región de saturación porque el drenaje no puede llenar ningún estado en el canal. La capacitancia cuántica aumenta en la región lineal a medida que el drenaje llena algunos estados —k, lo que lleva a errores en el cálculo de la corriente en el régimen lineal.
Observando que\(V_{T} = E_{C}/\eta^{0}q\) podemos reescribir la Ecuación (5.13.9) por encima del umbral como
Ahora, podemos simplificar la Ecuación (5.13.5) para darnos
\[ I=\frac{q W}{\pi^{2} \hbar^{2}} \int_{\mu_{s}-\eta q\left(V_{G s}-V_{T}\right)}^{\infty} \sqrt{2 m\left(E+\eta q\left(V_{G S}-V_{T}\right)\right)}\left(f\left(E, \mu_{S}\right)-f\left(E, \mu_{D}\right)\right) d E \nonumber \]
A T = 0K, podemos resolver la Ecuación (5.13.13) en el régimen lineal (\(V_{DS}<\eta(V_{GS}-V_{T})\)):
\[ I = \frac{qW}{\pi^{2}\hbar^{2}} \int^{\mu_{S}}_{\mu_{S}-qV_{DS}} \sqrt{2m(E-E_{C} + \eta qV_{GS}))}dE \nonumber \]
\( \frac{qW}{\pi^{2}\hbar^{2}} \sqrt{\frac{8m}{9}} (\eta q)^{3/2} \left[ (V_{GS}-V_{T})^{3/2}-(V_{GS}-V_{T}-V_{DS}/\eta)^{3/2} \right] \)
y en el régimen de saturación\((V_{DS} > \eta (V_{GS}-V_{T}))\):
\ [\ begin {alineado}
I &=\ frac {q W} {\ pi^ {2}\ hbar^ {2}}\ int_ {\ mu_ {s} -\ eta q\ izquierda (V_ {G S} -V_ {T}\ derecha)} ^ {\ mu_ {S}}\ sqrt {2 m\ izquierda (E+\ eta q\ izquierda (V_ {G S} -V_ {T}\ derecha)\ derecha)} d E\
&=\ frac {q W} {\ pi^ {2}\ hbar^ {2}}\ sqrt {\ frac {8 m} {9}} (\ eta q) ^ {3/2}\ izquierda (V_ {G S} -V_ {T}\ derecha) ^ {3/ 2}
\ end {alineado}\ nonumber\]
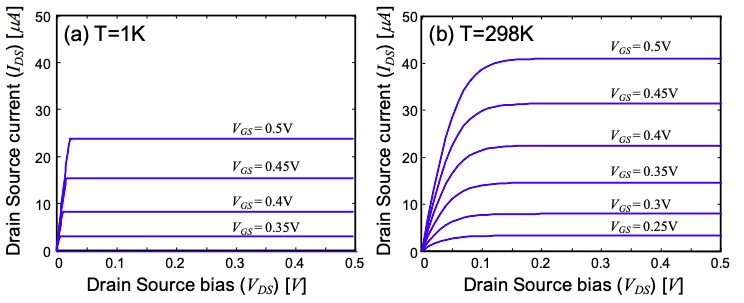
Tenga en cuenta que la corriente de saturación va\(\sim (V_{GS}-V_{T})^{3/2}\) en comparación con el transistor de nanocables balísticos, que va como\(\sim (V_{GS}-V_{T})\). Como veremos, el FET convencional tiene una dependencia de corriente de saturación de\(\sim (V_{GS}-V_{T})^{2}\).
MOSFET Convencionales
Finalmente, dirigimos nuestra atención a la columna vertebral de la electrónica digital, el transistor de efecto de campo semiconductor de óxido metálico no balístico (MOSFET).
El material del canal es un semiconductor masivo, típicamente silicio. Aquí, consideraremos un denominado MOSFET de canal n, lo que significa que la corriente del canal es transportada por electrones en la parte inferior de la banda de conducción del semiconductor.
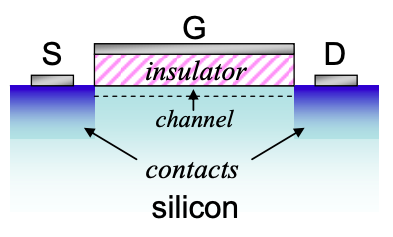
Ahora, consideremos los diversos regímenes operativos de un MOSFET convencional.
OFF: Subumbral\(V_{GS} < V_{T}\)
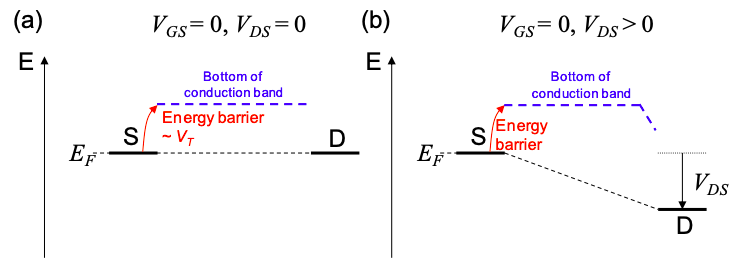
Similar al FET de alambre cuántico balístico, podemos modelar la corriente del canal como inyección sobre una barrera cercana al electrodo fuente.
Una vez más, definamos el voltaje umbral como la diferencia de potencial entre la energía de Fermi fuente y el mínimo de banda de conducción. \(^{†}\)
Como en el ejemplo balístico, cuando\(V_{GS} < V_{T}\), sólo la cola de la distribución de Fermi para los electrones en la fuente se solapa con estados vacíos en la banda de conducción. La corriente sigue la Ecuación (5.8.6).
\[ I = I_{0}\text{exp}\left[ \frac{qV_{GS}}{kT}\frac{C_{G}}{C_{ES}} \right] \nonumber \]
Las características del subumbral determinan el voltaje de puerta requerido para encender y apagar el FET. A partir de la Ec. (5.8.8) la pendiente subumbral es idealmente 60mV/década, lo que significa que un cambio de 60mV en el potencial de puerta corresponde a un cambio de década en la corriente del canal.
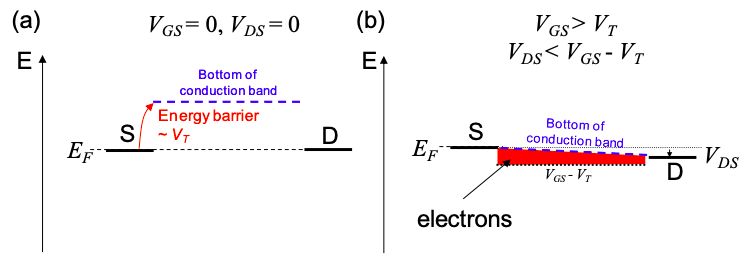
El régimen lineal:\(V_{GS} > V_{T},\ V_{DS} < V_{GS}-V_{T}\)
Como veremos, esto se conoce como el régimen lineal porque la corriente se escala linealmente con el potencial de la fuente de drenaje. Considera una rebanada delgada del canal con ancho W y largo\(\delta x\). Para que este análisis se mantenga, la longitud de esta porción no puede ser mucho más corta que la trayectoria libre media del electrón entre eventos de dispersión. En un transistor de silicio, hemos mostrado eso\(\delta x > 50 \text{nm}\) (ver el análisis asociado a la Figura 4.14.3). Los transistores de silicio con longitudes de canal más cortas que esta deben analizarse en el régimen balístico.
Dado que la densidad de estados por encima de la banda de conducción es muy grande en un semiconductor masivo, un MOSFET convencional entrará en el límite de carga fuerte/metálico para\((V_{GS} – V) > V_{T}\), es decir, el número de cargas\(\delta N\), en el corte es
\[ q \delta N = \frac{C_{G}}{A}W\delta x(V_{GS}-V-V_{T}) \nonumber \]
donde A = W.L es la superficie del canal.
Ahora la corriente dentro de la porción viene dada por
\[ I = \frac{q \delta N}{\tau} \nonumber \]
donde\(\tau\) es la vida útil de las portadoras dentro del segmento de canal.
Dado que la dispersión es importante, empleamos el modelo clásico de transporte de carga para relacionar la vida útil del portador de carga con la velocidad, v, y la longitud de la rebanada,\(\delta x\).
\[ I = q \delta N\frac{v}{\delta x} \nonumber \]
A continuación relacionamos la velocidad del portador de carga con la movilidad
\[ I = q \delta N\frac{\mu F}{\delta x} \nonumber \]
Ahora bien, debemos señalar que la dispersión hace que el potencial en el canal varíe con la posición. Definimos el potencial de canal V (x) en función de la posición en el canal. Así, expresando el campo eléctrico fuente-drenaje en términos del potencial de canal que tenemos
\[ I = q \frac{\mu}{\delta x}\delta N\frac{\delta V}{\delta x} \nonumber \]
A continuación, sustituimos la Ecuación (5.13.14) por la Ecuación (5.13.15), rindiendo
\[ I = \mu \frac{C_{G}}{L}(V_{GS}-V-V_{T})\frac{\delta V}{\delta x} \nonumber \]
Esto lo resolvemos bajo el límite de que\(\delta x \ll L\), integrando ambas partes con respecto a x. Dado que la corriente es uniforme en todo el canal, obtenemos:
\[ I.L = \int^{L}_{0} \mu \frac{C_{G}}{L}(V_{GS}-V-V_{T})\frac{dV}{dx} dx \nonumber \]
donde L es la longitud del canal. Es conveniente cambiar la variable de integración en el lado derecho a voltaje. En el régimen lineal, el potencial máximo del canal es\(V_{DS}\), por lo tanto:
\[ I = \mu \frac{C_{G}}{L^{2}}\int^{V_{DS}}_{0} (V_{GS}-V-V_{T})dV \nonumber \]
El régimen lineal requiere que todo el canal permanezca en el límite fuerte de carga/metálico. Esto ocurre si la puerta para drenar potencial,\(V_{GD}\), también excede\(V_{T}\)
\[ V_{GD}>V_{T} \nonumber \]
o podemos reescribir esto como
\[ V_{DS}<V_{GS}-V_{T} \nonumber \]
Bajo esta restricción, la ecuación (5.13.21) rinde
\[ I = \mu \frac{C_{G}}{L^{2}} \left( (V_{GS}-V_{T})V_{DS}-\frac{1}{2}V_{DS}^{2} \right) \nonumber \]
Es estándar expresar esto en términos de una capacitancia de puerta por unidad de área de canal,\(C_{OX}\):
\[ I = \mu \frac{W}{L}C_{OX} \left( (V_{GS}-V_{T})V_{DS}-\frac{1}{2}V_{DS}^{2} \right) \nonumber \]
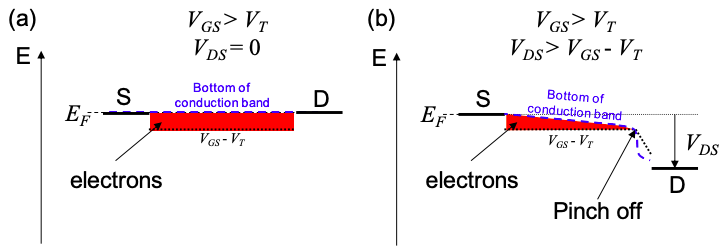
Saturación:\(V_{GS} > V_{T},\ V_{DS} > V_{GS}-V_{T}\)
Si el potencial de la puerta para drenar excede el umbral entonces la región del canal cercana al drenaje entra en el régimen de carga cero, caracterizado por un alto campo eléctrico y baja densidad de cargas móviles. Se dice que el canal pellizca y la corriente se satura porque ya no depende de él\(V_{DS}\). La fuerte región de carga/metálica termina cuando el potencial del canal local\(V = V_{GS} - V_{T}\)
\[ I = \int^{V_{GS}-V_{T}}_{0}\mu \frac{W}{L}C_{OX}(V_{GS}-V-V_{T})dV \nonumber \]
que da
\[ I = \mu \frac{W}{L}\frac{C_{OX}}{2}(V_{GS}-V_{T})^{2} \nonumber \]
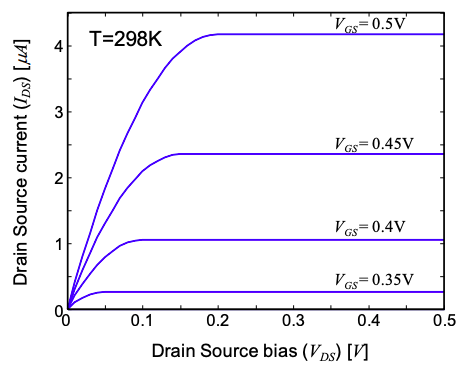
Las características IV de un MOSFET no balístico se muestran en la Figura 5.13.6.
\(^{†}\)En realidad, esto es una sobreestimación del voltaje umbral debido a que la densidad de estados en la banda de conducción es tan grande que el transistor a menudo se encenderá cuando el nivel de Fermi llegue a unos pocos kT. También ignora el efecto de la carga atrapada en la interfaz entre el canal y el aislante.


