12.1: Sistema de Muelle Masivo Sin Amortiguar

Última actualización
Guardar como PDF

Page ID: 84722

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

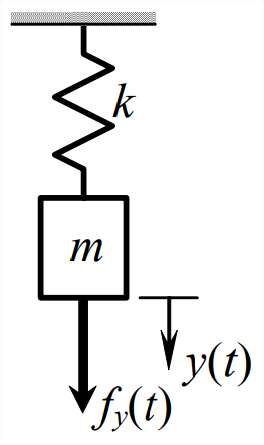
El tema de este capítulo es la vibración libre de los sistemas mecánicos no amortiguados, comenzando con el sistema de masa-resorte de un grado de libertad (1-DOF) de la Fig\(\PageIndex{1}\). Evaluamos el\(k\) sistema\(m\) - de manera más general en el Capítulo 7, pero lo volveremos a visitar aquí usando un enfoque diferente. La vibración libre puede surgir de la traslación inicial de la masa (relativa a la posición de equilibrio estático) y/o la velocidad inicial, y también de la excitación que ha cesado, lo que podría proporcionar a la masa tanto la traslación inicial como la velocidad inicial en el instante en que cesa la excitación. Sin embargo, es más fácil conceptualmente visualizar este movimiento como respuesta solo a una traslación inicial distinta de cero relativa a la posición de equilibrio estático. Hacerlo sacrifica un poco de generalidad porque tampoco podemos dar cuenta de una velocidad inicial distinta de cero, pero las características esenciales de la vibración libre son reveladas por este enfoque. Considere un sistema de masa-resorte sin amortiguar con traslación inicial distinta de cero\(y(0)=y_{0}\),, y velocidad inicial cero\(\dot{y}(0)=0\), pero sin forzar la excitación, de modo que\(f_{y}(t)=0\). De la Ecuación 7.1.2, la ODE de vibración libre es

\[m \ddot{y}+k y=f_{y}(t)=0\label{eqn:12.1} \]

Ahora hacemos las preguntas: ¿Puede existir el movimiento en la forma y\(y(t)=Y \cos \omega t\), de ser así, cuáles son las constantes\(Y\) y\(\omega\)? Para encontrar las respuestas, sustituimos la presunta forma de movimiento en Ecuación ODE\(\ref{eqn:12.1}\), realizamos las diferenciaciones y álgebra, y vemos a dónde conduce el proceso:

\[m\left(-\omega^{2} Y \cos \omega t\right)+k Y \cos \omega t=\left(-\omega^{2} m+k\right) Y \cos \omega t=0 \nonumber \]

Esta ecuación puede satisfacerse en general, para una solución no trivial, solo si

\[\omega^{2}=k / m \equiv \omega_{n}^{2} \Rightarrow \omega=\omega_{n}=\sqrt{k / m} \nonumber \]

Además, podemos usar la condición inicial para encontrar\(Y\):

\[y(0)=y_{0}=Y \cos (\omega \times 0)=Y \nonumber \]

\[\Rightarrow \quad y(t)=y_{0} \cos \omega_{n} t\label{eqn:12.2} \]

Este simple resultado ya se derivó en la Ecuación 7.3.1; lo volvemos a derivar de manera diferente aquí solo para establecer el enfoque que será útil a continuación para los sistemas de orden superior.