2.5: Modelos de señal pequeña

Última actualización
Guardar como PDF

Page ID: 86459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Para crear el modelo lineal, necesitamos introducir el concepto de sesgo, y el comportamiento del dispositivo de señal grande y pequeña señal. Considera el siguiente circuito, mostrado en la Figura\(\PageIndex{1}\). Estamos aplicando la suma de dos voltajes al diodo\(V_{B}\), el voltaje de polarización (que se supone que es un voltaje de CC), y\(v_{s}\), el voltaje de la señal (que se supone que es CA, o sinusoidal). Por definición, asumiremos que\(\left| v_{s} \right|\) es mucho menor que\(\left| V_{B} \right|\). Como resultado de estos voltajes, habrá una corriente\(I_{D}\) que fluye a través del diodo. Esta consistirá en dos corrientes:\(I_{B}\), la llamada corriente de polarización, y\(i_{s}\), que será la corriente de señal. Nuevamente, asumimos que\(i_{s}\) es mucho más pequeño que\(I_{B}\).

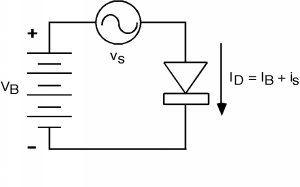
Un circuito contiene una fuente de voltaje V_B, una fuente de voltaje sinusoidal v_s y un diodo en serie. La corriente que fluye a través del diodo de ánodo a cátodo es I_D, que es la suma de I_B e i_s. — Figura\(\PageIndex{1}\): Ensamblar un sesgo de señal grande y una excitación de CA de señal pequeña

Lo que nos gustaría hacer es ver si podemos encontrar una relación lineal entre\(v_{s}\) y\(i_{s}\), que podríamos utilizar en nuestro análisis de señales. Hay dos formas en las que podemos atacar el problema: un enfoque gráfico y un enfoque puramente matemático. Probemos primero el enfoque gráfico, ya que es más intuitivo, y luego confirmaremos lo que averigüemos con un método matemático.

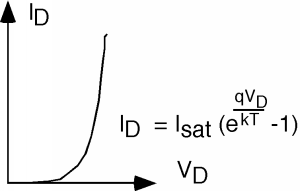
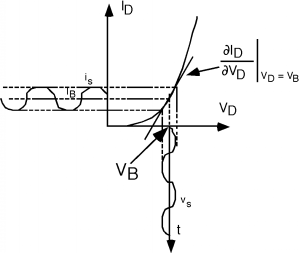
Recordemos\(I \text{-} V\) las características de un diodo (Figura\(\PageIndex{2}\)). En la situación actual,\(V_{D}\) es la suma de dos voltajes: un voltaje de polarización de CC\(V_{B}\) y una señal de CA,\(v_{s}\). Vamos a trazar\(V_{D} (t)\) sobre el\(V_{D}\) eje como se muestra en la Figura\(\PageIndex{3}\).

Gráfica de corriente de diodo en ejes I_D vs V_D. La ecuación gráfica viene dada por e (el exponente natural) a la potencia de q V_D sobre kT, menos 1, el todo multiplicado por I_sat. — Figura\(\PageIndex{2}\):\(I \text{-} V\) Comportamiento del diodo

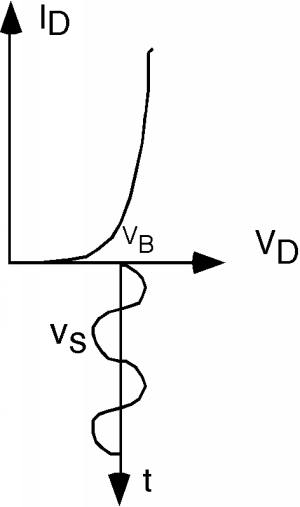
Plano de coordenadas estándar del primer cuadrante con V_D en el eje x e I_D en el eje y, mostrando la gráfica de V_B como una función de crecimiento exponencial a partir del origen. Un tercer eje vertical del tiempo se extiende hacia abajo desde un punto en el eje V_D, siendo la dirección del tiempo creciente hasta el fondo. Una función sinusoidal de v_s se muestra en los ejes V_D vs t. — Figura\(\PageIndex{3}\): Sesgo y excitación de señal de una\(I \text{-} V\) curva de diodo

¿Cómo vamos a averiguar cuál es la corriente? Lo que tenemos que hacer es proyectar el voltaje hacia arriba en la curva I-V característica, y luego proyectarlo sobre el eje de corriente vertical. Esto lo hacemos en Figura\(\PageIndex{4}\).

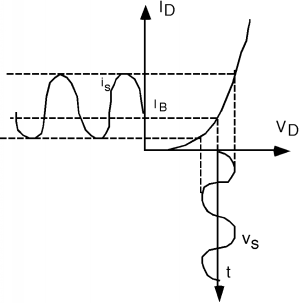
El gráfico de la Figura 3 anterior tiene una línea punteada vertical cada una extendiéndose hacia arriba desde el eje t, el mínimo de la función v_s y el máximo de la función v_s. Las líneas verticales se extienden hacia arriba hasta que se cruzan con la gráfica V_B, y luego se extienden horizontalmente hacia la izquierda. Una función sinusoidal delimitada por las líneas horizontales superior e inferior se extiende hacia la izquierda, comenzando en la línea punteada central donde intersecta el eje I_D en el valor I_B. Se eleva hacia la izquierda, alcanzando un valor máximo de i_s, y luego cae a un valor mínimo que está más cerca de la línea punteada I_B que la i _s la línea es. — Figura\(\PageIndex{4}\): Copiar y Pegar Leyenda aquí. (Copyright; autor vía fuente)

Tenga en cuenta que la señal de corriente de salida está algo distorsionada, lo que significa que aún no tenemos un comportamiento lineal. Redujamos la amplitud del voltaje de la señal, como se muestra en la Figura\(\PageIndex{5}\). Ahora vemos dos cosas: a) la salida está mucho menos distorsionada, por lo que debemos obtener un comportamiento más lineal, y b) podríamos obtener la amplitud de la señal de salida\(i_{s}\) simplemente multiplicando la señal de entrada\(v_{s}\) por la pendiente de la curva I-V en el punto donde el dispositivo está sesgado. Hemos reemplazado la curva I-V no lineal del diodo por una lineal, que es aplicable en el rango de la tensión de la señal.

\[i_{s} = \left. \frac{\partial}{\partial V_{D}} \left(V_{D}\right) \right| _{I_{D} = I_{B}} \nonumber \]

La Figura 4 anterior se repite con una función v_s de menor magnitud, lo que lleva a que las líneas punteadas horizontales que se extienden fuera de ella para estar más espaciadas por igual. El valor de i_s, la línea horizontal superior, es igual a la derivada parcial de la curva I_D-VS-V_D evaluada donde el valor de V_D es V_B. — Figura\(\PageIndex{5}\): Con una señal más pequeña, la respuesta es más lineal

Para obtener la pendiente, necesitamos algunas ecuaciones simples:\[I_{D} = I_{\text{sat}} \left( e^{\frac{q V_{D}}{kT}} - 1 \right) \simeq I_{\text{sat}} e^{\frac{q V_{D}}{kT}} \nonumber \]

\[ \frac{\partial}{\partial V_{D}} \left(I_{D}\right) = \frac{q}{kT} I_{\text{sat}} e^{\frac{q V_{D}}{kT}} \nonumber \]

Cuando evaluamos la derivada parcial a voltaje\(V_{D}\), observamos que\[I_{\text{sat}} e^{\frac{q V_{D}}{kT}} = I_{B} \nonumber \]

y por lo tanto, la pendiente de la curva es justa\(\frac{q}{kT} I_{B}\) o\(40 I_{B}\), ya que\(\frac{q}{kT}\) solo tiene un valor de\(40 \mathrm{~V}^{-1}\) a temperatura ambiente. Tenga en cuenta que la corriente dividida por voltaje es solo la conductancia, (que es solo la inversa de la resistencia) y así hemos encontrado la pequeña conductancia lineal de señal para el diodo.

En lo que respecta al generador de señal de CA, podríamos reemplazar el diodo por una resistencia cuyo valor sea el inverso de la conductancia, o bien\(r = \frac{1}{40} I_{B}\), donde\(I_{B}\) está la corriente de polarización de CC a través del diodo.

Los estudiantes a veces se confunden acerca de cómo podemos reemplazar un diodo, que solo conduce en una dirección, con una resistencia, que conduce en ambos sentidos. La respuesta es mirar cuidadosamente a la Figura\(\PageIndex{5}\). A medida que el voltaje de la señal de CA sube y baja, la corriente de salida de CA también aumenta y disminuye de la misma manera. En el rango limitado de los parámetros de la señal de CA, el diodo es de hecho un elemento de señal lineal, no uno rectificador, ya que lo es para aplicaciones de señales grandes.

Ahora vamos a obtener la misma respuesta desde un enfoque puramente matemático. \[I_{D} = I_{B} + i_{s} = I_{\text{sat}} \left( e^{\frac{q V_{D}}{kT}} - 1 \right) \simeq e^{\frac{q \left( V_{B}+v_{s} \right)}{kT}} \nonumber \]

En la última expresión, bajamos la\(-1\) ya que es muy pequeña en comparación con el término exponencial y se puede descuidar.

Ahora señalamos que:\[e^{\frac{q \left( V_{B}+v_{s} \right)}{kT}} = e^{\frac{q V_{B}}{kT}} e^{\frac{q v_{s}}{kT}} \nonumber \]

Y, para el segundo exponencial, si\(q V_{B}\) es mucho menor que\(kT\),\[e^{\frac{q V_{s}}{kT}} \simeq 1 + \frac{q v_{s}}{kT} + \ldots \nonumber \]

donde hemos utilizado la expansión de la serie power para el exponencial, pero sólo hemos tomado los dos primeros términos. Así\[I_{B} + i_{s} \simeq I_{\text{sat}} e^{\frac{q V_{B}}{kT}} \left( 1 + \frac{q v_{s}}{kT} \right) \nonumber \]

Obviamente\[I_{B} = I_{\text{sat}} e^{\frac{q V_{B}}{kT}} \nonumber \]

y\[\begin{array}{l} i_{s} &= I_{\text{sat}} e^{\frac{q V_{B}}{kT}} \left( \frac{q}{kT} v_{s} \right) \\ &= \frac{q}{kT} I_{B} v_{s} \end{array} \nonumber \]

lo que nos da el mismo resultado que antes:\[\frac{i_{s}}{v_{s}} = \frac{q}{kT} I_{B} \nonumber \]