4.5: Segunda Ley de Fick
- Page ID
- 86486
Tomando el derivado respecto a\(x\) la primera ley de Fick\[\frac{\text{d}}{\text{d} x} (\text{Flux}) = - \left( D \frac{\partial^{2} N(x, t)}{\partial x_{2}^{ 2}} \right)\]
y luego sustituyendo la ecuación de continuidad en ella, tenemos la segunda ley de difusión de Fick:\[\frac{\partial N(x, t)}{\partial t} = D \frac{\partial^{2} N(x, t)}{\partial x_{2}^{ 2}}\]
Se trata de una ecuación de difusión estándar, y una que aparece una y otra vez cuando se trata de tales fenómenos.
Para obtener una solución a la ecuación de difusión, primero debemos asumir algunas condiciones de límite. Nos ocuparemos de una oblea semi-infinita, y asumiremos que\[\lim_{x \rightarrow \infty} N(x, t) = 0\]
Esta es una suposición razonable, ya que a lo sumo nuestra difusión solo penetrará una micra más o menos en la oblea, y toda la oblea en sí tiene varios cientos de micras de espesor.
También tenemos que decidir algo sobre las condiciones iniciales. Haremos la suposición de que tenemos en el momento\(t=0\) y\(x=0\) alguna concentración superficial de impurezas que llamaremos\(Q_(0)\), medida en\(\frac{\mathrm{impurities}}{\mathrm{cm}^2}\). Esta es la situación que tendríamos si introduciéramos las impurezas usando un paso de implante relativamente poco profundo. Una condición alternativa de límite superficial sería aquella en la que la concentración de impurezas permanece en algún valor fijo. Esto es lo que sucede cuando hay impurezas en el flujo de gas sobre la oblea durante el tiempo que están en el horno de difusión. A esto se le llama difusión de fuente infinita.
La primera condición se llama difusión de fuente limitada, y eso es lo que consideraremos más adelante aquí. No es demasiado difícil demostrar que con esta condición inicial, la solución a la ecuación de difusión es:\[N(x, t) = \frac{Q_{0}}{\sqrt{\pi Dt}} e^{- \frac{x^{2}}{4Dt}}\]
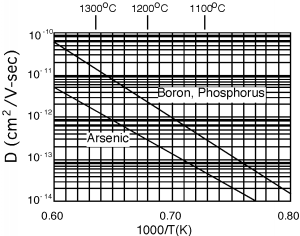
Tenga en cuenta que\(N(x, t)\) es una función de la distancia en la oblea\(x\) y el tiempo\(t\). El tiempo es, por supuesto, el tiempo del proceso de difusión. \(D\), la constante de difusión, depende de la temperatura a la que tenga lugar la difusión. La figura\(\PageIndex{1}\) es una gráfica\(D\) de tres de los dopantes más utilizados en silicio. El fósforo y el boro son los aceptores y donantes más comunes respectivamente. A veces se usa arsénico porque es significativamente más grande en diámetro que el fósforo o el boro, y así se mueve menos después de un implante.

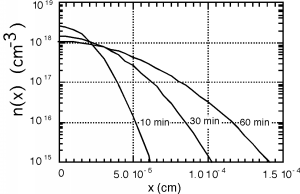
Supongamos que hacemos un implante relativamente poco profundo de boro en nuestra oblea tipo p, y depositamos un\(Q_{0}\) de\(5 \times 10^{13}\) fósforo\(\frac{\mathrm{atoms}}{\mathrm{cm}^2}\). Luego realizamos una difusión de recocido\(1100 ^{\circ} \mathrm{C}\) durante 60 minutos. A\(1100 ^{\circ} \mathrm{C}\),\(D\) para el fósforo parece estar a punto\(2 \times 10^{-13} \ \frac{\mathrm{cm}^2}{\mathrm{sec}}\). Haremos una trama de\(N(x)\) para varias épocas. Si haces esto en casa, asegúrate de poner tiempo en segundos, no minutos, horas o quincenas. Mirando Figura\(\PageIndex{2}\), es bastante fácil ver cómo las impurezas se mueven hacia el semiconductor, y cómo la concentración en la superficie,\(N(0, t)\), disminuye a medida que más y más de las impurezas se mueven más profundamente en la oblea.