6.15: Coincidencia de un solo trozo

Última actualización
Guardar como PDF

Page ID: 86576

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A menudo, hay razones por las que usar un inductor o condensador discreto para emparejar no es una buena idea. En las frecuencias altas donde la coincidencia es importante, las pérdidas tanto en L como en C significan que no obtienes una buena coincidencia, y la mayoría de las veces (a excepción de algunos capacitores ajustables por aire dieléctrico) es difícil obtener justo el valor que deseas.

Sin embargo, hay otro enfoque. Una línea de transmisión en cortocircuito o abierta, cuando se ve en su entrada parece una reactancia pura o susceptancia pura. Con un corto como carga, el coeficiente de reflexión tiene magnitud de unidad $| Γ | = 1.0$ y así nos movemos por el exterior de la Gráfica Smith a medida que la longitud de la línea aumenta o disminuye, y $\frac{Z_{en}}{Z_{0}}$ es puramente imaginario. Cuando hicimos la transformación bilineal a partir del $\frac{Z (s)}{Z_{0}}$ avión a la $r (s)$ plano, el eje imaginario se transformó en el círculo de diámetro 2, que terminó siendo el círculo exterior que definió la Gráfica Smith.

Otra forma de ver esto es volver a esta ecuación. Allí encontramos:

Z (s) = Z_{0} \frac{Z_{L} + i Z_{0} bronceado (β s)}{Z_{0} + i Z_{L} bronceado (β s)}

Con $Z_{L} = 0$ esto reduce a

Z (s) = i Z_{0} bronceado (β s)

Que, por supuesto para diversos valores de $s$ , puede tomar cualquier valor de $i \infty$ a $- (i \infty)$ . No tenemos que ir a Radio Shack© y comprar un montón de inductores y capacitores diferentes. ¡Podemos simplemente conseguir alguna línea de transmisión y acortarla en varios lugares!

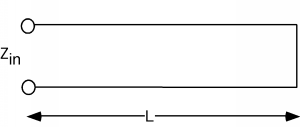
Así, en lugar de un componente discreto, podemos usar una sección de línea de transmisión en cortocircuito (o abierta) en su lugar Figura. Estas líneas coincidentes se denominan talones coincidentes. Una de las principales ventajas aquí es que con una línea que tiene un corto ajustable en el extremo de la misma, podemos obtener cualquier reactancia que necesitemos, simplemente ajustando la longitud del trozo. Cómo funciona todo esto se volverá obvio después de que echemos un vistazo a un ejemplo.

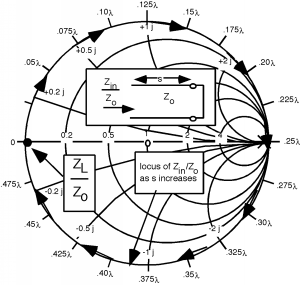
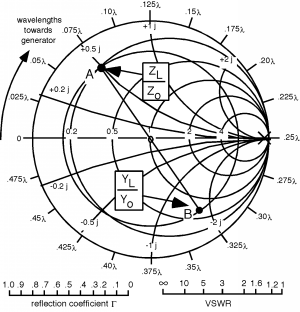
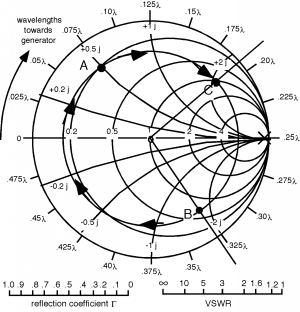
Hagamos una. En la Figura podemos ver que, $\frac{Z_{L}}{Z_{0}} = 0.2 + 0.5 i$ , por lo que marcamos un punto “A” en la Gráfica Smith. Ya que vamos a querer poner el stub de afinación o coincidencia en shunt a través de la línea, lo primero que haremos es convertir $\frac{Z_{L}}{Z_{0}}$ en una admisión normalizada $\frac{Y_{L}}{Y_{0}}$ por ir $180^{°}$ alrededor de la Gráfica Smith hasta el punto “B”, donde $\frac{Y_{L}}{Y_{0}} ≂ 0.7 + -1.7 i$ . Ahora giramos alrededor en el radio constante, $r (s)$ círculo hasta que golpeamos el círculo coincidente en el punto “C”. Esto se muestra en la Figura. En “C”, $\frac{Y_{S}}{Y_{0}} = 1.0 + 2.0 i$ . Usando un gráfico Smith “real”, obtengo que la distancia de rotación es de aproximadamente $0.36 λ$ . Recuerde, todo el camino alrededor es $\frac{λ}{2}$ , así que muy a menudo puedes “hacer un globo ocular” sobre lo lejos que tienes que llegar, y hacerlo es un buen control para cometer un estúpido error matemático. Si la distancia no se ve bien en el Smith Chart, ¡probablemente cometiste un error!

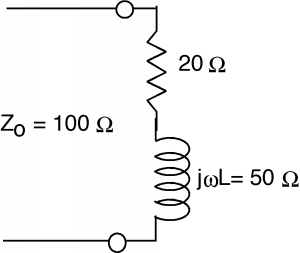
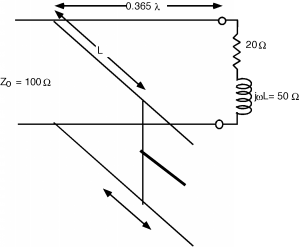
Bien, en este punto, la parte real de la admisión es la unidad, así que todo lo que tenemos que hacer es agregar un talón para cancelar la parte imaginaria. Como se mencionó anteriormente, los talones suelen venir con ajustables, o “cortos deslizantes” para que podamos hacerlos de la longitud que queramos Figura.

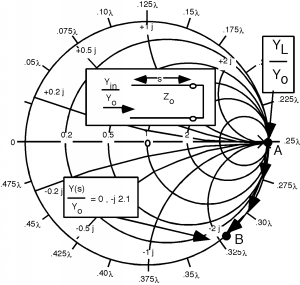
Nuestra tarea ahora, es decidir cuánto empujar o tirar del mango deslizante en el talón, para obtener la reactancia que queremos. El indicio sobre lo que debemos hacer está en Figura. El extremo del trozo es un cortocircuito. ¿Cuál es la admisión de un cortocircuito? Respuesta: $\infty$ , $i \infty$ ! ¿Dónde está esto en el Smith Chart? Respuesta: en el exterior, en el lado derecho en el eje real. Ahora, si empezamos en un corto, y empezamos a hacer la línea más larga que $s = 0$ , lo que le pasa $\frac{Y (s)}{Y_{0}}$ ? Se mueve por el exterior del Smith Chart. Lo que tenemos que hacer es alejarnos del corto hasta llegar $\frac{Y (s)}{Y_{0}} = - (i 2.0)$ y sabremos cuánto tiempo debe ser el stub de afinación en cortocircuito Figura. Al pasar de “A” a “B” atravesamos una distancia de aproximadamente $0.07 λ$ y así es donde debemos establecer la posición del corto deslizante sobre el trozo Figura.

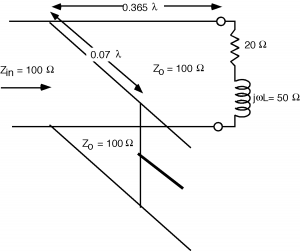
A veces pensamos que la acción del talón de afinación nos permite movernos a lo largo del $ℜ (\frac{Y (s)}{Y_{0}})$ para llegar al centro de la Gráfica Smith, o a una Figura de coincidencia. No estamos en este caso, moviéndonos físicamente por la línea. Más bien nos estamos moviendo por un contorno de constante parte real porque todo lo que el talón puede hacer es cambiar la parte imaginaria de la admisión, ¡no puede hacer nada a la parte real!