6.16: Coincidencia de Doble Stub

Última actualización
Guardar como PDF

Page ID: 86561

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hay una última técnica que podemos observar que es algo más flexible que la coincidencia de talón único que acabamos de ver. ¡Esto se llama coincidencia de doble talón! Supongamos que tenemos la siguiente situación, como se representa en la figura. Hay una carga de $\frac{Z_{L}}{Z_{0}} = 0.2 + 1.3 i$ ubicado al final de la línea, y luego a cierta distancia arbitraria ( $0.11 λ$ ) un trozo ajustable. Otro (arbitrario) $0.11 λ$ desde el primer talón, hay un segundo. Vamos a trazar $\frac{Y_{L}}{Y_{0}}$ en el Smith Chart, y luego, dado que los talones están en derivación a través de la línea, cambie a admisión y encuentre $\frac{Y_{L}}{Y_{0}}$ . Es fácil ver que $\frac{Y_{L}}{Y_{0}} = 1.5 + 2.3 i$ .

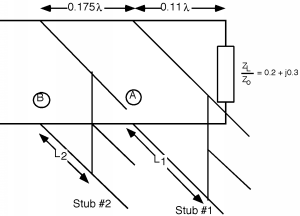
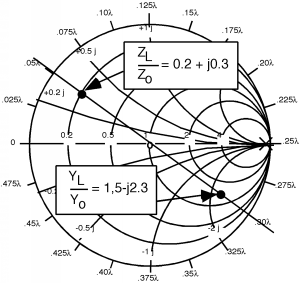
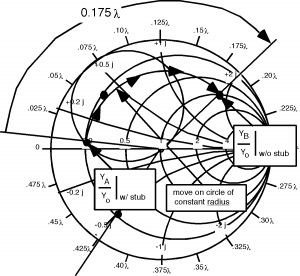
Lo primero que bien podríamos hacer es bajar al primer talón, y ver qué admisión tenemos ahí Figura. Pasamos de la carga, al primer trozo girando sobre un círculo de radio constante (constante $| r (s) |$ ) ya que lo único que estamos haciendo es ir de un lugar en la línea a otro. Si llamamos a la ubicación en la línea del primer talón “A”, entonces podemos ver que $\frac{Y_{A}}{Y_{0}} = 0.25 + 0.6 i$ .

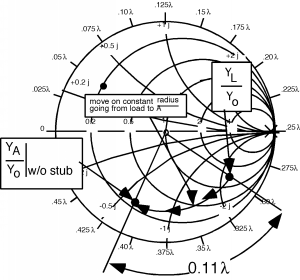
Ahora bien, ¿qué puede lograr el primer talón? Un talón cortocircuitado puede crear cualquier admisión imaginaria que queramos, pero no puede cambiar la parte real de la admisión. Así, ajustando el primer trozo, podemos movernos en un círculo de parte real constante $0.25 Y_{0}$ , y tener cualquier parte imaginaria que queramos. Esto se muestra esquemáticamente aquí.

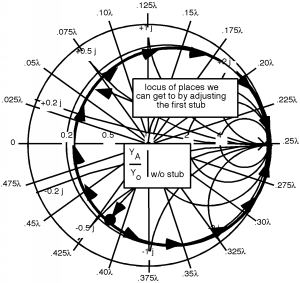
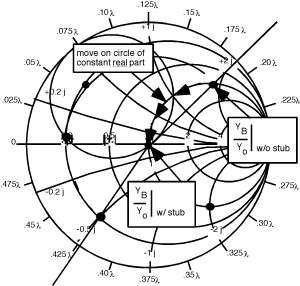
Ahora, ¿a dónde queremos ir? Bueno, nos gustaría terminar en algún lugar para que, después de haber pasado de A a B en la línea (pasado del primer trozo al segundo), estemos en el círculo coincidente. Si esto fuera así, entonces, ya que estamos en el círculo coincidente, podríamos usar el segundo trozo para hacer coincidir toda la línea y ya estaríamos hechos.

Esto es complicado ahora, así que hay que prestar atención y pensar. Si quiero encontrar un lugar que, al pasar de A a B, termine en el círculo coincidente, entonces lo que debo hacer es tomar el círculo coincidente y moverlo de B a A. Es decir, si giro el círculo coincidente alrededor $0.175 λ$ hacia la carga, entonces cualquier lugar en ese círculo coincidente girado está garantizado para terminar en el círculo coincidente real, cuando vamos $0.175 λ$ de vuelta hacia el generador.

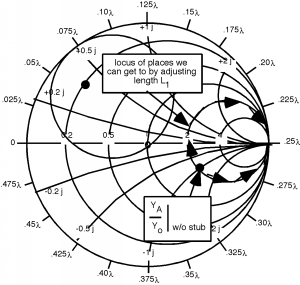
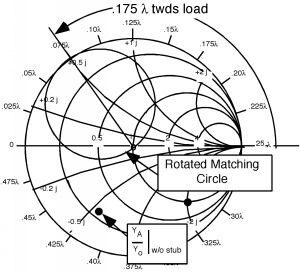
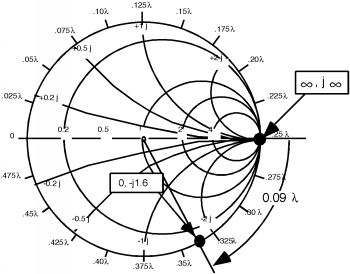
Bien, así que esto es lo que hacemos. Primero, giramos el círculo coincidente 0.175 alrededor hacia la carga (ir en sentido antihorario) Figura. Ahora lo que tenemos que hacer es de alguna manera obtener $\frac{Y_{A}}{Y_{0}}$ sin talón a algún lugar del círculo coincidente girado. La única manera de hacerlo es cambiar la parte imaginaria de $Y_{A}$ con el talón. Supongamos que nos movemos como se muestra en Figura. Al pasar de $\frac{Y_{A}}{Y_{0}}$ sin talón a $\frac{Y_{A}}{Y_{0}}$ con stub hemos cambiado la parte imaginaria de $- (i 0.6)$ a $i 0.05$ , por lo que hemos añadido $i 0.65$ a la parte imaginaria de $\frac{Y_{A}}{Y_{0}}$ . Por lo tanto, usando nuestro método estándar para encontrar la longitud del primer trozo, comenzamos en $\infty$ , $- \infty$ (el corto al final del talón) y dar la vuelta al exterior del Smith Chart hasta que encontremos $i 0.05$ . Para llegar de un lugar a otro fuimos $(0.25 + 0.09) λ = 0.34 λ$ y así la longitud del primer trozo, $L_{1}$ debería ser $0.09 λ$ . Ahora estamos en $\frac{Y_{A}}{Y_{0}}$ con talón. Lo siguiente que tenemos que hacer es rotar otro $0.175 λ$ hacia el generador para que podamos llegar al talón B. Al hacer esta rotación, nuevamente nos mantenemos en un círculo de radio constante, porque ahora nos estamos moviendo hacia abajo por la línea de transmisión no sumando reactancia mediante el uso de un trozo! Esta rotación está garantizada para terminarnos en el círculo coincidente porque cada punto en el círculo girado (el que partimos) es exactamente $0.175 (λ)$ hacia la carga desde el círculo coincidente. Como se muestra aquí, ahora estamos en el punto $\frac{Y_{B}}{Y_{0}}$ sin talón $1.0 + 1.6 i$ . Por lo tanto, necesitamos ajustar la longitud $L_{2}$ del segundo talón para darnos $- (i 1.6)$ de reactancia, para que podamos movernos (a lo largo de un círculo de parte real constante = 1.0) hacia el centro de la Gráfica Smith. Tenemos que encontrar la longitud $L_{2}$ para el segundo trozo, ¡pero eso ya es fácil! (Figura)

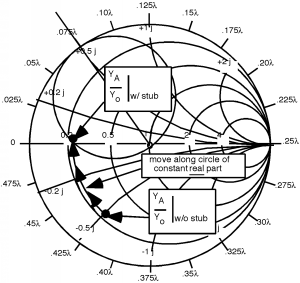
Así, al hacer doble coincidencia de stub, podemos, al agregar el grado adicional de libertad de dos talones ajustables, no tener que especificar exactamente dónde se tienen que colocar los talones, para que puedan estar en la línea antes de que sea el emparejamiento intentó. Aquí está toda la secuencia de cambios que hicimos. Vea si puede comenzar en “Inicio” y pasar por los números $0 \to 5$ y obtener de $\frac{Z_{L}}{Z_{0}}$ al punto coincidente en el centro de la Gráfica Smith. Recuerde, cuando nos movemos de un lugar a otro en la línea, debemos permanecer en un círculo de radio constante. Cuando cambiamos la reactancia ajustando un trozo, debemos movernos a lo largo de círculos de parte real constante. Si haces eso, ¡es fácil!

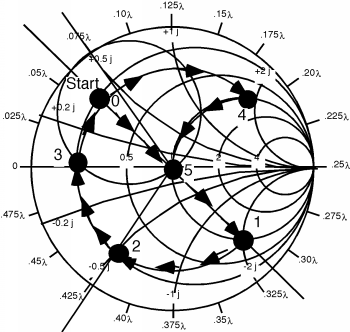
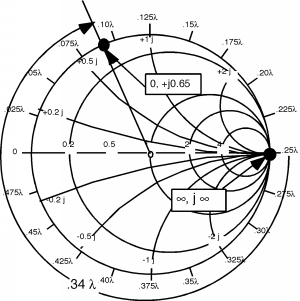
Sólo hay un pequeño problema. ¿Qué pasa si $\frac{Y_{A}}{Y_{0}}$ sin talón había terminado como se muestra aquí. Estamos en el $ℜ (\frac{Y_{A}}{Y_{0}} | sin talón) = 2.0$ círculo. No importa lo duro que lo intente, y no importa donde me ponga $L_{1}$ todo lo que puedo hacer es dar vueltas en el círculo pequeño como se muestra, y nunca terminaré en el círculo coincidente girado, ¡y no podré hacer una coincidencia! Bueno, si agrego un tercer trozo... ¡te dejaré resolverlo!