Apéndice 1: Circuitos eléctricos y leyes de interconexión
- Page ID
- 86525
Un circuito conecta elementos de circuito juntos en una configuración específica diseñada para transformar la señal fuente (que se origina a partir de una fuente de voltaje o corriente) en otra señal, la salida, que corresponde a la corriente o voltaje definido para un elemento de circuito en particular. Un circuito resistivo simple se muestra en la Figura\(A1.1\) a continuación. Este circuito es la realización eléctrica de un sistema que tiene su entrada proporcionada por un sistema fuente que produce\(v_{\text{in}}(t)\).
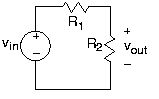 a)
a)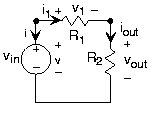 b)
b) c)
c)Para entender lo que logra este circuito, queremos determinar el voltaje a través de la resistencia etiquetada por su valor\(R_{2}\). Refundiendo matemáticamente este problema, necesitamos resolver algún conjunto de ecuaciones para que relacionemos el voltaje de salida con el voltaje\(v_{\text{out}}\) de la fuente. Sería simple —un poco demasiado simple en este punto— si pudiéramos anotar instantáneamente la única ecuación que relaciona estos dos voltajes. Hasta que tengamos más conocimiento sobre cómo funcionan los circuitos, debemos escribir un conjunto de ecuaciones que nos permitan encontrar todos los voltajes y corrientes que se puedan definir para cada elemento del circuito. Debido a que tenemos un circuito de tres elementos, tenemos un total de seis voltajes y corrientes que deben especificarse o determinarse. Puede definir las direcciones para el flujo de corriente positiva y la caída de voltaje positiva de la manera que desee. Una vez calculados los valores para los voltajes y corrientes, pueden ser positivos o negativos según tu definición. Cuando dos personas definen variables de acuerdo a sus preferencias individuales, los signos de sus variables pueden no estar de acuerdo, pero los valores de flujo de corriente y caída de voltaje para cada elemento coincidirán. Recuerda al definir tus variables de voltaje y corriente que las\(v \text{-} i\) relaciones para los elementos presumen que el flujo de corriente positivo está en la misma dirección que la caída de voltaje positiva. Una vez que defina voltajes y corrientes, necesitamos seis ecuaciones no redundantes para resolver las seis tensiones y corrientes desconocidas. Al especificar la fuente, tenemos una; esto equivale a proporcionar la\(v \text{-} i\) relación de la fuente. Las\(v \text{-} i\) relaciones para las resistencias nos dan dos más. Estamos sólo a mitad de camino; ¿de dónde sacamos las otras tres ecuaciones que necesitamos?
Lo que necesitamos para resolver cada problema del circuito son declaraciones matemáticas que expresen cómo se interconectan los elementos del circuito. Dicho de otra manera, necesitamos las leyes que rigen la conexión eléctrica de los elementos del circuito. En primer lugar, los lugares donde los elementos del circuito se unen entre sí se denominan nodos. Dos nodos se indican explícitamente en la Figura\(A.1.1b\); un tercero está en la parte inferior donde se\(R_{2}\) conectan la fuente de voltaje y la resistencia. Los ingenieros eléctricos tienden a dibujar diagramas de circuitos —esquemas— de manera rectilínea. Por lo tanto, la larga línea que conecta la parte inferior de la fuente de voltaje con la parte inferior de la resistencia está destinada a hacer que el diagrama se vea bonito. Esta línea simplemente significa que los dos elementos están conectados entre sí. Las leyes de Kirchhoff, una para voltaje y otra para corriente, determinan lo que significa una conexión entre elementos de circuito. Estas leyes son esenciales para analizar este y cualquier circuito. Ellos llevan el nombre de Gustav Kirchhoff, un físico alemán del siglo XIX.
Ley Actual de Kirchhoff
En cada nodo, la suma de todas las corrientes que entran o salen de un nodo debe ser igual a cero. Lo que esta ley significa físicamente es que la carga no puede acumularse en un nodo; lo que entra debe salir. En el ejemplo de la Figura\(A1.1b\) anterior, tenemos un circuito de tres nodos y así tenemos tres ecuaciones KCL. \[\begin{align} (-i) - i_{1} &= 0 \\ i_{1} - i_{2} &= 0 \\ i + i_{2} &= 0 \end{align}\]
Tenga en cuenta que la corriente que ingresa a un nodo es la negativa de la corriente que sale del nodo.
Dadas dos cualesquiera de estas ecuaciones de KCL, podemos encontrar la otra sumando o restándolas. Así, una de ellas es redundante y, en términos matemáticos, podemos descartar a cualquiera de ellas. La convención es descartar la ecuación para el nodo (sin etiquetar) en la parte inferior del circuito.
Al escribir ecuaciones KCL, encontrarás que en un circuito\(n\) -node, exactamente una de ellas siempre es redundante. ¿Puedes esbozar una prueba de por qué esto podría ser cierto? Pista: Tiene que ver con el hecho de que la carga no se acumulará en un solo lugar por sí sola.
- Solución
-
KCL dice que la suma de corrientes que entran o salen de un nodo debe ser cero. Si consideramos dos nodos juntos como un “supernodo”, KCL se aplica también a las corrientes que ingresan a la combinación. Dado que ninguna corriente ingresa a un circuito completo, la suma de corrientes debe ser cero. Si tuviéramos un circuito de dos nodos, la ecuación KCL de uno debe ser la negativa del otro, podemos combinar todos menos uno de los nodos en un circuito en un supernodo; KCL para el supernodo debe ser el negativo de la ecuación KCL del nodo restante. En consecuencia, al especificar ecuaciones\(n-1\) KCL siempre se especifica la restante.
Ley de Voltaje (KVL) de Kirchhoff
La ley de voltaje dice que la suma de voltajes alrededor de cada bucle cerrado en el circuito debe ser igual a cero. Un bucle cerrado tiene la definición obvia: Comenzando en un nodo, trazar una ruta a través del circuito que le devuelve al nodo de origen. KVL expresa el hecho de que los campos eléctricos son conservadores: El trabajo total realizado para mover una carga de prueba alrededor de una trayectoria cerrada es cero. La ecuación KVL para nuestro circuito es\[v_{1} + v_{2} - v = 0\]
Al escribir ecuaciones KVL, seguimos la convención de que el voltaje de un elemento entra con un signo más al atravesar el camino cerrado, pasamos del positivo al negativo de la definición del voltaje.
Para nuestro circuito de ejemplo, tenemos tres\(v \text{-} i\) relaciones, dos ecuaciones KCL y una ecuación KVL para resolver los seis voltajes y corrientes del circuito. \[\begin{align} v \text{-} i: \quad\quad & v = v_{\text{in}} \\ & v_{1} = R_{1} i_{1} \\ & v_{\text{out}} = R_{2} i_{\text{out}} \\[4pt] \text{KCL:}\quad &(-i) - i_{1} = 0 \\ & i_{1} - i_{\text{out}} = 0 \\[4pt] \text{KVL:} \quad & -v + v_{1} + v_{\text{out}} = 0 \end{align}\]
¡Tenemos exactamente el número correcto de ecuaciones! Eventualmente, descubriremos atajos para resolver problemas de circuito; por ahora, queremos eliminar todas las variables pero\(v_{\text{out}}\) y determinar cómo depende de\(v_{\text{in}}\) y de los valores de resistencia. La ecuación KVL se puede reescribir como\(v_{\text{in}} = v_{1} + v_{\text{out}}\). Sustituyendo en ella la\(v \text{-} i\) relación de la resistencia, tenemos\(v_{\text{in}} = R_{1} i_{1} + R_{2} i_{\text{out}}\). Sí, eliminamos temporalmente la cantidad que buscamos. Aunque no es obvio, es la forma más sencilla de resolver las ecuaciones.
Dice una de las ecuaciones de KCL\(i_{1} = i_{\text{out}}\), lo que significa que\(v_{\text{in}} = R_{1} i_{\text{out}} + R_{2} i_{\text{out}} = \left(R_{1} + R_{2}\right) i_{\text{out}}\). Resolviendo para la corriente en la resistencia de salida, tenemos\(i_{\text{out}} = \frac{v_{\text{in}}}{R_{1} + R_{2}}\). Ahora hemos resuelto el circuito: hemos expresado una tensión o corriente en términos de fuentes y valores de elementos de circuito. Para encontrar cualquier otra cantidad de circuito, podemos volver a sustituir esta respuesta en nuestras ecuaciones originales o las que desarrollamos en el camino. Usando la\(v \text{-} i\) relación para la resistencia de salida, obtenemos la cantidad que buscamos. \[v_{\text{out}} = \frac{R_{2}}{R_{1} + R_{2}} v_{\text{in}}\]
Refiriéndose de nuevo a la Figura\(A1.1\), un circuito debe servir para algún propósito útil. ¿Qué tipo de sistema realiza nuestro circuito y, en términos de valores de elementos, cuáles son los parámetros del sistema?
- Solución
-
El circuito sirve como amplificador que tiene una ganancia de\(\frac{R_{2}}{R_{1} + R_{2}}\).

