1.9: Combinaciones Lineales de Ondas
- Page ID
- 84434
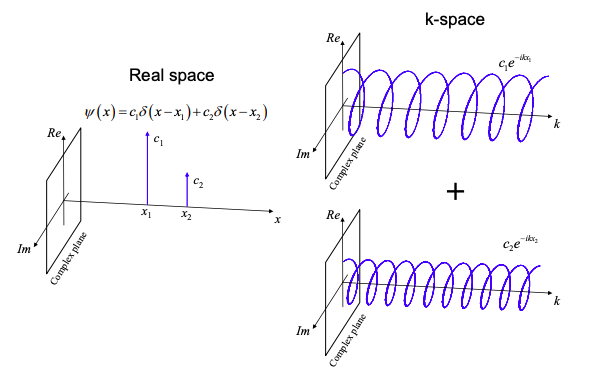
A continuación, consideramos las combinaciones de diferentes funciones exponenciales complejas. Por ejemplo, en la Figura 1.9.1 trazamos una función de onda que podría describir un electrón que es equiprobable en posición\(x_{1}\) y posición\(x_{2}\). La representación k-espacio es simplemente la superposición de dos funciones exponenciales complejas correspondientes a\(x_{1}\) y\(x_{2}\). \(^{†}\)
\[ \psi(x)=c_{1}\delta(x-x_{1})+c_{2}(x-x_{2}) \Leftrightarrow A(\omega) = c_{1}e^{-ikx_{1}}+c_{2}e^{-ikx_{2}} \nonumber \]
También podemos generalizar a una distribución arbitraria de posiciones,\(\psi(x)\). Si\(\psi(x)\) describe un electrón, por ejemplo, la probabilidad de que el electrón esté localizado en la posición x es\(|\psi(x)|^{2}\). Así, en el espacio k el electrón es descrito por la suma de exponenciales complejos\(e^{-ikx}\) cada uno oscilando en k-espacio y ponderado por amplitud\(\psi(x)\).
\[ A(k)=\int^{+\infty}_{-\infty}\psi(x)e^{-ikx}dx \nonumber \]
Esto puede reconocerlo a partir de 6.003 como una transformada de Fourier. Del mismo modo, la transformada inversa es
\[ \psi(x)=\frac{1}{2\pi}\int^{+\infty}_{-\infty}A(k)e^{ikx}dk \nonumber \]
Para convertir entre tiempo y frecuencia angular, utilice
\[ A(\omega) =\int^{+\infty}_{-\infty} \psi(t)e^{i\omega t}dt \nonumber \]
y
\[ \psi(t)=\frac{1}{2\pi}\int^{+\infty}_{-\infty} A(\omega)e^{-i\omega t}d\omega \nonumber \]
Tenga en cuenta que los factores de\(\frac{1}{2\pi}\) están presentes cada vez que se integra con respecto a k o\(\omega\). Tenga en cuenta también que al convertir entre exponenciales complejos y funciones delta, la siguiente identidad es útil:
\[ 2\pi\delta(u)=\int^{+\infty}_{-\infty} \text{exp}[iux]dx \nonumber \]
\(^{†}\)Tenga en cuenta que esta función de onda no es realmente normalizable.


