1.28: El límite que\(V_{0} \rightarrow \infty\) (the infinite square well)

En las paredes donde el potencial es infinito, vemos a partir de la Ecuación (1.27.2) que las soluciones decaen inmediatamente a cero desde entonces\(\alpha \rightarrow \infty\). Así, en la región clásicamente prohibida del pozo cuadrado infinito\(\psi=0\).

La función ondulada es continua, por lo que debe acercarse a cero en las paredes. Una posible solución con ceros en el límite izquierdo es

\[ \psi(x)=A\ sin(k(x+L/2)) \nonumber \]

donde k se elige de tal manera que ψ = 0 en el límite derecho también:

\[ kL=n\pi \nonumber \]

Para normalizar la función de onda y determinar A, integramos:

\[ \int_{-\infty}^{+\infty}|\psi(x)|^{2} d x=\int_{-L / 2}^{L / 2} A^{2} \cos ^{2}(n \pi x / L+n \pi / 2) d x \nonumber \]

De donde determinamos que

\[ A = \sqrt{2/L} \nonumber \]

La energía se calcula a partir de la Ecuación (1.25.3)

\[ E = \frac{\hbar^{2}k^{2}}{2m}=\frac{\hbar^{2}\pi^{2}n^{2}}{2mL^{2}} \nonumber \]

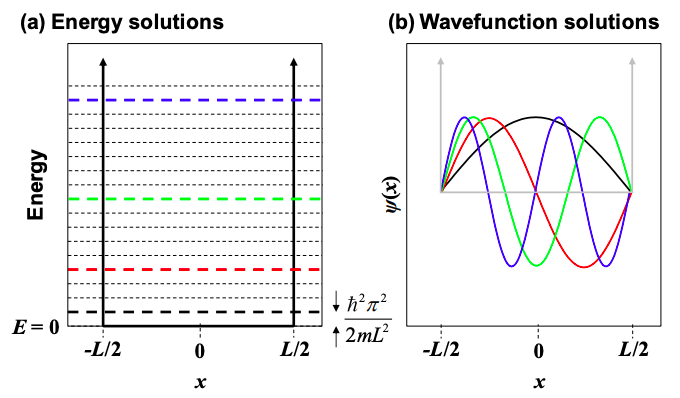
Las primeras energías y funciones de onda de electrones en el pozo se representan en la Figura 1.28.1.

Dos características de las soluciones merecen comentario:

1. Se cuantifican los estados ligados en el pozo — sólo se permiten ciertos niveles de energía.
2. Los niveles de energía escalan inversamente con\(L^{2}\). A medida que la caja se hace más pequeña cada nivel de energía y las brechas entre los niveles de energía permitidos se hacen mayores.

Figura\(\PageIndex{1}\):. Los cuatro estados más bajos para un solo electrón en un pozo cuadrado infinito. Tenga en cuenta que hemos trazado ψ (x) no\(|ψ(x)|^{2}\).