1.29: El Pozo Cuadrado Finito
- Page ID
- 84576
Cuando el potencial de confinamiento es finito, ya no podemos asumir que la función de onda es cero en los límites del pozo. Para un potencial de confinamiento finito, la función de onda penetra en la barrera: cuanto menor es el potencial de confinamiento, mayor es la penetración.
De la Ecuación (1.27.1) la solución general para la función de onda dentro del pozo fue
\[ \psi(x)=A\ cos(kx)+B\ sin(kx) , \nonumber \]
pero a partir de las soluciones para el pozo infinito, podemos ver que, dentro del pozo, la ondulación parece
\[ \psi(x)=A\ cos(kx) \nonumber \]
o
\[ \psi(x)=A\ sin(kx) \nonumber \]
La simplificación es posible porque el potencial del pozo es simétrico alrededor de x = 0. Así, la densidad de probabilidad también\(|ψ(x)|^{2}\) debe ser simétrica,\(^{†}\) y de hecho tanto ψ (x) = sin (kx) y ψ (x) = cos (kx) tienen distribuciones de probabilidad simétricas aunque ψ (x) = sin (kx) es una función de onda antisimétrica.
Consideraremos las soluciones simétricas (cos (kx)) y antisimétricas (sin (kx)) por separado.
Función de onda simétrica
Podemos asumir una solución de la forma:
\ [\ psi (x) =\ left\ {\ begin {array} {ll}
e^ {\ alpha x} &\ text {para} x\ Leq-L/2\\
A\ cos (k x) &\ text {para} -L/2\ leq x\ leq L/2\
e^ {-\ alpha x} &\ text {para} x\ geq L/2
\ fin {array}\ derecho. \ nonumber\]
donde
\[ k = \sqrt{\frac{2mE}{\hbar^{2}}} \nonumber \]
y
\[ \alpha = \sqrt{\frac{2m(V_{0}-E)}{\hbar^{2}}} \nonumber \]
Tenga en cuenta que la solución como está escrita no está normalizada. Podemos normalizarlo después.
El siguiente paso es evaluar la constante A haciendo coincidir las soluciones por partes en el borde del pozo. Solo necesitamos considerar un borde, porque ya hemos fijado la simetría de la solución.
En el borde derecho, igualar la amplitud de la función de onda da
\[ \psi(L/2)=A\ cos(kL/2) = \text{exp}[-\alpha L/2] \nonumber \]
Equiparar la pendiente de la ondulaciónfunción da
\[ \psi’(L/2)=-kA\ sin(kL/2) = -\alpha\ \text{exp}[-\alpha L/2] \nonumber \]
Dividiendo la ecuación (1.29.8) por la ecuación (1.29.7) para eliminar A da
\[ tan(kL/2)=\alpha /k \nonumber \]
Pero\(\alpha\) y k son ambas funciones de la energía
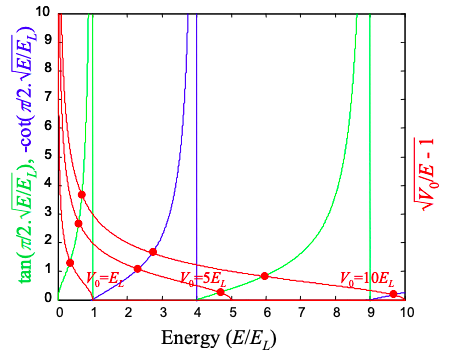
\[ tan(\frac{\pi}{2}\sqrt{\frac{E}{E_{L}}}) = \sqrt{\frac{V_{0}-E}{E}} \nonumber \]
donde hemos definido la energía infinita del estado de tierra del pozo cuadrado
\[ E_{L}=\frac{\hbar^{2}\pi^{2}}{2mL^{2}} \nonumber \]
Como en el caso del pozo cuadrado infinito, encontramos que sólo ciertos, discretos, valores de energía dan una solución. Una vez más, se cuantifican las energías de los estados de electrones en el pozo. Para obtener las energías necesitamos resolver la Ecuación (1.29.10). Desafortunadamente, esta es una ecuación trascendental, y debe resolverse numérica o gráficamente. Trazamos las soluciones en la Figura 1.29.1.
Función de onda antisimétrica
Las soluciones antisimétricas se encuentran de manera similar a las soluciones simétricas. Primero asumimos una solución antisimétrica de la forma:
\ [\ psi (x) =\ left\ {\ begin {array} {ll}
e^ {\ alpha x} &\ text {para} x\ Leq-L/2\\
A\ sin (k x) &\ text {para} -L/2\ leq x\ leq L/2\
-e^ {-\ alpha x} &\ text {para} x\ geq L/2
\ end {array}\ right. \ nonumber\]
Luego, evaluamos la constante A haciendo coincidir las soluciones por partes en el borde del pozo. Nuevamente, solo necesitamos considerar un borde, porque ya hemos fijado la simetría de la solución.
En el borde derecho, igualar la amplitud de la función de onda da
\[ \psi(L/2)=A\ sin(kL/2)=-\text{exp}[-\alpha L/2] \nonumber \]
Equiparar la pendiente de la ondulaciónfunción da
\[ \psi’(L/2)=kA\ cos(kL/2)=\alpha\ \text{exp}[-\alpha L/2] \nonumber \]
Dividiendo la ecuación (1.29.8) por la ecuación (1.29.7) para eliminar A da
\[ cot(kL/2)=-\alpha /k \nonumber \]
Expansión\(\alpha\) y k en términos de energía
\[ -cot(\frac{\pi}{2}\sqrt{\frac{E}{E_{L}}}) = \sqrt{\frac{V_{0}-E}{E}} . \nonumber \]
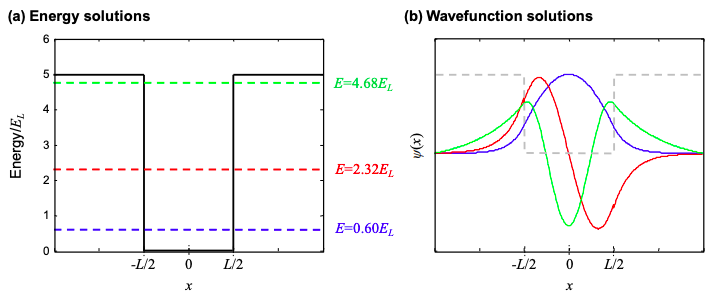
En la Figura 1.29.1, resolvemos para la energía. Tenga en cuenta que siempre hay al menos una solución ligada sin importar cuán superficial sea el pozo. En la Figura 1.29.2 trazamos las soluciones para un potencial de confinamiento\(V_{0}=5.E_{L}\).