2.8: El DOS 0-D - Moléculas Individuales y Puntos Cuánticos Confinados en 3-D

El DOS 0-d es un caso especial porque la partícula está confinada en todas las direcciones.

Al igual que una partícula en un pozo con niveles de energía discretos, podríamos suponer que la densidad de estados en un 0-d podría ser una serie de funciones delta a los niveles de energía permitidos. Esto es cierto para una partícula aislada de 0-d.

La vida útil de una carga en una órbita de una partícula aislada es infinita. Desde el principio de incertidumbre, las vidas infinitas se asocian con estados energéticos perfectamente discretos en la molécula aislada, es decir\(\Delta t \rightarrow \infty\), si,\(\Delta E \rightarrow 0\).

Pero cuando, por ejemplo, una molécula se pone en contacto con un electrodo metálico, el electrón eventualmente puede escapar al metal. Ahora, la vida útil del electrón en la molécula es finita y, por lo tanto, los niveles de energía de la molécula también deberían exhibir un ancho finito. Por lo tanto, los niveles de energía molecular se amplían en un sistema de metal-molécula acoplada, cuanto mayor sea el acoplamiento, mayor será la ampliación de los niveles de energía molecular.

Supongamos que hay dos electrones en el orbital molecular. Supongamos que la vida útil de estos electrones en la molécula es\(\tau\). Además, supongamos que la desintegración de la probabilidad de electrones en la molécula es exponencial. Entonces la dependencia temporal de la probabilidad de electrones en el orbital molecular es:

\[ |\psi(t)|^{2}=\frac{2}{\tau}\text{exp} \left[ -\frac{t}{\tau} \right]u(t) \nonumber \]

Una opción para la función de onda correspondiente es

\[ \psi(t)=\sqrt{\frac{2}{\tau}}\text{exp} \left[ -i\frac{E_{0}t}{\hbar}-\frac{t}{2\tau} \right]u(t) \nonumber \]

Hemos incluido un término complejo en el exponente para dar cuenta de la rotación de fase del electrón. La frecuencia angular característica de la rotación de fase es\(E_{0}/\hbar\), donde\(E_{0}\) está la energía del orbital molecular en la molécula aislada.

A continuación utilizamos una transformada de Fourier para convertir del tiempo al dominio energético. La transformada de Fourier\(\psi(t)\) da

\[ A(\omega) = \frac{\sqrt{2/\tau}}{1/2\tau +i(E_{0}/\hbar-\omega)} \nonumber \]

Ahora a partir de la definición de normalización en frecuencia angular requerimos que

\[ \frac{1}{2 \pi} \int_{-\infty}^{\infty}|A(\omega)|^{2} d \omega=\int_{-\infty}^{\infty} g(E) d E \nonumber \]

donde g (E) es la densidad de estados. Por lo tanto,

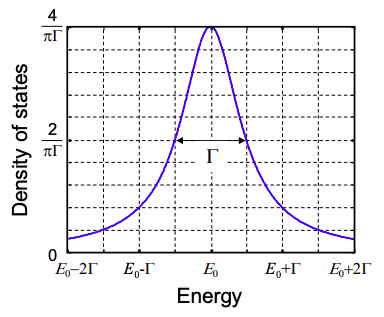
\[ g(E)=\frac{1}{2 \pi}|A(\omega)|^{2} \frac{d \omega}{d E}=\frac{2}{\pi} \frac{\hbar / 2 \tau}{\left(E-E_{0}\right)^{2}+(\hbar / 2 \tau)^{2}} \nonumber \]

Esta función es conocida como lorentziana — es característica de una decadencia exponencial en el dominio del tiempo; ver Figura 2.8.1. El ancho del lorentziano a la mitad de su valor pico (ancho completo a la mitad máximo, o FWHM) es\(\hbar/\tau\). El acoplamiento entre la molécula y el contacto puede describirse ya sea por la vida útil del electrón en la molécula\(\tau\), o por una energía de acoplamiento\(\Gamma\), igual a la FWHM de la densidad de estados lorentziana y dada por

\[ \Gamma=\hbar/\tau \nonumber \]

Así, como era de esperar, una interacción más fuerte entre una molécula y un contacto se correlaciona con una vida útil más corta del electrón en la molécula y una densidad molecular más amplia de estados. En sistemas bien acoplados\(\Gamma\) puede acercarse a 1 eV, correspondiente a una vida útil del electrón de\(\tau \sim 4fs\).

Figura\(\PageIndex{1}\): La densidad de estados en una molécula se amplía cuando la molécula se pone en contacto con un metal. El efecto es significativo si la molécula es pequeña, y la vida útil de los electrones en la molécula cambia drásticamente en presencia del metal.