2.15: Problemas

Última actualización
Guardar como PDF

Page ID: 84365

Marc Baldo
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

i) Usando MATLAB, generar Figura 2.7.2

ii) Si\(L_{y} = L_{x} \cdot \sqrt{\frac{3}{5}}\) qué modo tiene una energía menor {\(n_{x}= 3,n_{y} = 1\)} o {\(n_{x}= 2, n_{y} = 2\)}

2. El transistor ilustrado a continuación tiene un espesor de óxido (\(\epsilon = 4\epsilon_{0}\)) d = 1.2nm y profundidad de canal\(L_{z}\) = 2.5nm. Considerando el canal como un pozo cuántico, ¿cuántos modos se llenan cuando se aplica un voltaje V = 1V a la puerta?

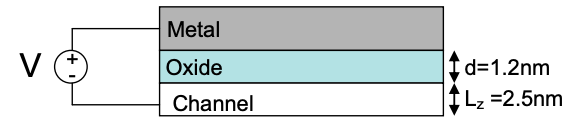
Captura de pantalla 2021-04-20 a las 21.19.55.png — Figura\(\PageIndex{28}\): Un modelo sencillo de un transistor moderno.

Sugerencia: calcular la carga en el canal usando la expresión para un condensador de placa paralela.

3. Un conductor particular de longitud L tiene la relación de dispersión:

\ [\ begin {array} {l}
E_ {1} (k) =5+2 V\ cos (k a)\\
E_ {2} (k) =10-2 V\ cos (k a)
\ end {array}, |k|<\ frac {\ pi} {a}\ nonumber\]

donde V y a son constantes positivas.

i) Esbozar la relación de dispersión.

ii) Calcular la densidad de estados en términos de E, V y a.

4. En general, la aproximación degenerada para la función de distribución de electrones\(f(E,E_{F})\) funciona cuando la densidad de estados es grande y varía lentamente por encima y por debajo del nivel de Fermi. La aproximación no degenerada funciona mejor cuando la densidad de estados en el nivel Fermi es mucho menor que la densidad de estados a energías superiores.

Aquí, consideramos estas aproximaciones en una densidad gaussiana de estados. El gaussiano varía bastante lentamente cerca de su centro, pero disminuye extremadamente rápido en sus colas. La población de electrones en una densidad gaussiana de estados viene dada por

\[ n = \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\frac{1}{2}(E/\sigma)^{2}}f(E,E_{F})dE \nonumber \],

donde\(f(E,E_{F})\) está la función Fermi. Para un rango particular del nivel de Fermi,\(E_{F}\), la población de electrones puede aproximarse como:

\[ n \approx \int^{E_{F}}_{-\infty} \frac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\frac{1}{2}(E/\sigma)^{2}}dE \nonumber \]

Este es el límite degenerado.

A medida que disminuye el nivel de Fermi, la población de electrones se calcula mejor en el límite no degenerado. Derivar el nivel mínimo de Fermi\(E_{F}\) para que el límite degenerado se mantenga en función de la temperatura T y la desviación estándar\(\sigma\).

Sugerencia: estimar el nivel mínimo de Fermi examinando la distribución energética de electrones en el límite no degenerado.