4.1: Dispositivos de cable cuántico de dos terminales
- Page ID
- 84532
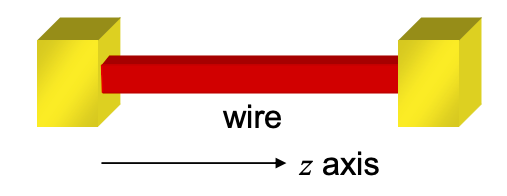
Consideremos un cable cuántico entre dos contactos. Como vimos en la Parte 2, un cable cuántico es un conductor unidimensional. Aquí, asumiremos que el alambre tiene la misma geometría que la estudiada en la Parte 2: una sección transversal rectangular con área Lx.Ly. Los electrones están confinados por un potencial infinito fuera del cable, y solo pueden fluir a lo largo de su longitud; elegidos arbitrariamente como el eje z en la Figura 4.1.1.
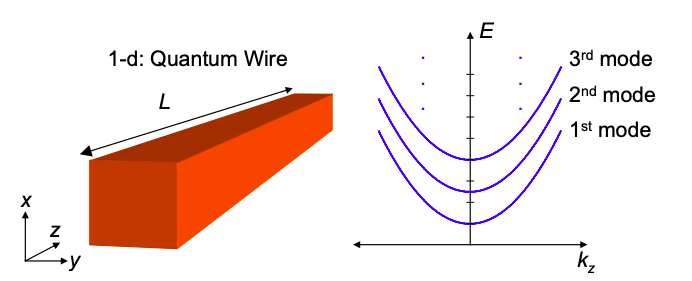
Bajo estos supuestos, si modelamos los electrones por ondas planas en la dirección z obtenemos
\[ E=\frac{\pi^{2}\hbar^{2}}{2m} \left( \frac{n^{2}_{x}}{L^{2}_{x}} +\frac{n^{2}_{y}}{L^{2}_{y}} \right) + \frac{\hbar^{2}k_{z}^{2}}{2m}, \ \ \ n_{x},n_{y} = 1,2,… \nonumber \]
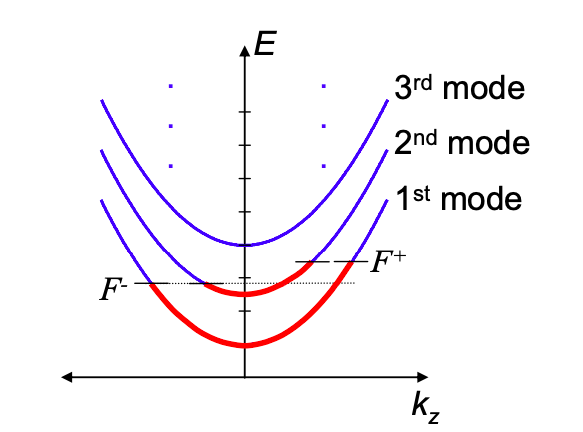
Recordemos que para que la corriente fluya debe haber diferencia en el número de electrones en\(+k_{z}\) y\(-k_{z}\) estados. Al igual que en la Parte 2, definimos dos cuasi niveles de Fermi:\(F^{+}\) para estados con\(k_{z}>0\),\(F^{-}\) para estados con\(k_{z}<0\). Así, la corriente fluye cuando los electrones que viajan en la dirección +z están en equilibrio entre sí, pero no con electrones viajando en la dirección —z. Por ejemplo, en la Figura 4.1.3, la corriente es transportada por los electrones no compensados en los\(+k_{z}\) estados.