4.10: El Drude o Modelo Semiclásico de Transporte de Carga

Los modelos cuánticos de conducción de carga rara vez se aplican fuera de la nanoelectrónica. Para aplicaciones tradicionales, el modelo semiclásico del físico alemán Paul Drude suele ser suficiente. Drude propuso que los conductores contienen iones positivos inmóviles incrustados en un mar de electrones. A diferencia de la visión cuántica, donde esos electrones ocupan diversos estados con diferentes energías, Drude vio a los electrones como indistinguibles.

En el modelo cuántico de transporte de carga, la corriente es transportada solo por esa fracción de electrones cercana a la energía Fermi. Los electrones portadores de corriente se mueven aproximadamente a la velocidad Fermi,\(v_{F} = \hbar k_{F}/m\). Los electrones restantes son compensados, es decir, el flujo de números iguales en cada dirección no produce corriente neta.

Figura\(\PageIndex{1}\): La aplicación de un campo eléctrico desplaza los cuasi niveles de Fermi para electrones que se mueven con el campo (\(F^{+}\)) y contra el campo (\(F^{-}\)).

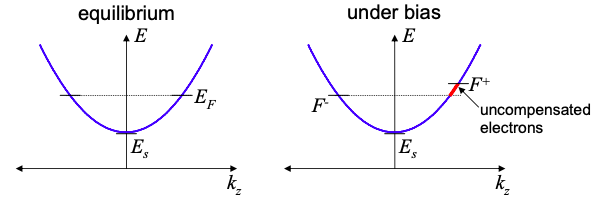
Pero en el modelo Drude, la corriente es transportada por todos los electrones, moviéndose a una velocidad promedio conocida como la velocidad de deriva,\(\textbf{v}_{d}\). Así, el modelo clásico fundamental para la conducción de carga es

\[ \textbf{J}= qn\textbf{v}_{d} \nonumber \]

donde n es la densidad de electrones.

En el modelo Drude, todos los electrones viajan en dirección al campo eléctrico, recogiendo energía del campo. Eventualmente cada electrón choca con algo, un ion positivo u otro electrón, momento en el cual, el electrón se detiene. Luego es acelerado una vez más por el campo eléctrico, viajando de esta manera stop-start a través del conductor.

Figura\(\PageIndex{2}\): Trayectorias electrónicas a través de sitios de dispersión. El tiempo promedio entre colisiones es el tiempo de relajación,\(\tau_{m}\).

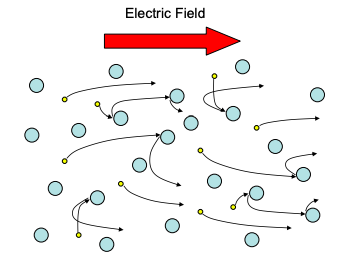
La conductividad del material se caracteriza por\(\tau_{m}\), el tiempo de relajación, el tiempo medio entre colisiones.

La velocidad a la que los electrones ganan impulso del campo,\(\epsilon\) debe ser igual a la tasa de pérdidas debidas a la dispersión:\(^{†}\)

\[ \left. \frac{d\textbf{p}}{dt} \right|_{\text{scattering}} = \left. \frac{d\textbf{p}}{dt} \right|_{\text{field}} \nonumber \]

\[ \frac{mv_{d}}{\tau_{m}} = q\epsilon , \nonumber \]

Reordenando la ecuación (4.11.3), podemos expresar la velocidad de deriva y la densidad de corriente en términos del tiempo de relajación.

\[ \textbf{J} = \frac{nq^{2}\tau_{m}}{m}\epsilon \nonumber \]

Comparando con la ley de Ohm (expresada en términos de la conductividad,\(\sigma = 1/\rho\))

\[ \textbf{J} = \sigma \epsilon \nonumber \]

donde

\[ \sigma = \frac{nq^{2}\tau_{m}}{m} \nonumber \]

\(^{†}\)Esta derivación sigue a Ashcroft y Mermin, “Solid State Physics”, Saunders College Publishing (1976).