4.12: Masa efectiva
- Page ID
- 84561
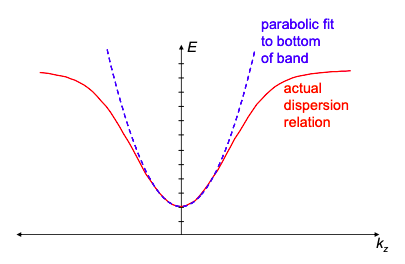
Hasta ahora, tanto los modelos clásicos como los cuánticos de conducción han asumido que los electrones portadores de corriente ocupan estados puros de onda plana. La relación de dispersión de materiales reales, sin embargo, varía de la parábola ideal. Podemos aproximar cualquier relación de dispersión por una onda plana si permitimos que la masa del electrón varíe. Llamamos a la masa modificada la masa efectiva. Bajo esta aproximación, se piensa que el electrón es una partícula clásica y diversos fenómenos complejos se envuelven en la masa efectiva. Por ejemplo, dada la relación de dispersión E (k), una expansión de Taylor alrededor de k = 0 rinde:
\[ \left. E(k) = E(0)+k\frac{dE}{dk} \right|_{k=0} \left. + \frac{1}{2}k^{2}\frac{d^{2}E}{dk^{2}} \right|_{k=0} + … \nonumber \]
Aproximar la relación de dispersión por una onda plana da
\[ E(k) = E_{0} + \frac{\hbar^{2}k^{2}}{2m^{*}} \nonumber \]
Equiparando los términos cuadráticos en ecuaciones. (4.13.1) y (4.13.2) obtenemos una expresión para la masa efectiva
\[ m^{*} = \hbar^{2}\left( \frac{d^{2}E}{dk^{2}} \right)^{-1} \nonumber \]
El concepto de masa efectiva se usa comúnmente en modelos clásicos de transporte de electrones, especialmente modelos de movilidad como la Ecuación (4.12.2).