4.13: Comparando los modelos cuánticos y semiclásicos de conducción Drude

El camino libre medio

El modelo Drude da una imagen físicamente incorrecta de la conducción de carga. Sin embargo funciona bastante bien. El modelo cuántico muestra que en lugar de que todos los electrones se muevan a la velocidad de deriva, como en el modelo Drude, solo los electrones no compensados que transportan corriente, cada uno se mueve aproximadamente a la velocidad Fermi:\(^{3}\) Así, el modelo Drude puede reorganizarse como

\[ J = qn^{‘}v_{F} \]

donde la densidad de carga no compensada es

\[ n^{‘} = n\frac{v_{d}}{v_{F}} \]

También podemos definir la trayectoria libre media\(L_{m}\), como la distancia promedio que recorre un electrón entre eventos de dispersión. La trayectoria libre media se relaciona con la velocidad de Fermi por:

\[ L_{m} = v_{F}\ \tau_{m} \]

Curiosamente, la trayectoria libre media es aproximadamente igual a la longitud característica\(L_{0}\) en la derivación de la ley de Ohm.

Flujo de corriente de equilibrio y no equilibrio

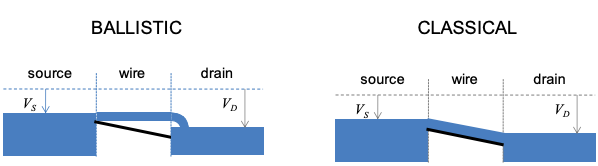
Podemos demostrar las diferencias entre los límites clásicos y balísticos utilizando la analogía del flujo de agua de un reservorio a otro. La aplicación de sesgo a través de un cable equivale a disminuir la altura del depósito de drenaje en relación con el depósito de origen. En el modelo balístico, el agua que fluye desde la fuente viaja a través del cable como un chorro antes de relajarse al equilibrio en el drenaje. En el modelo clásico el agua minimiza su potencial en canal.

Figura\(\PageIndex{1}\): Una analogía del flujo de agua para el flujo de corriente balístico y clásico. En el límite clásico, el agua está siempre en equilibrio local con el canal.

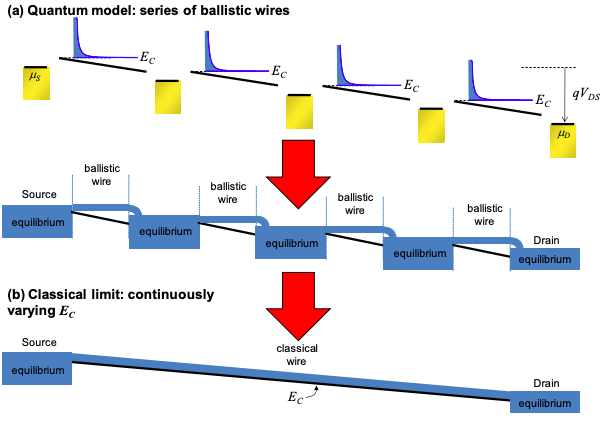
Una forma de pensar sobre el transporte clásico es como el límite de una serie de cables balísticos a nanoescala intercalados por contactos. Por definición, los electrones en los contactos están en equilibrio. Así, los contactos son diferentes a los dispersores elásticos que consideramos anteriormente, porque los electrones cambian de energía en los contactos. El caso limitante de muchos contactos muy próximos es un borde de banda de conducción continuamente variable; ver Figura 4.14.2.

Figura\(\PageIndex{2}\): En un cable clásico, el borde de la banda de conducción varía continuamente con la posición. El modelo clásico puede imaginarse como el caso limitante de muchos dispositivos balísticos en serie.

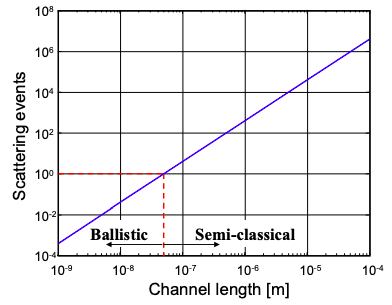
La escala de longitud de la conducción balística

Para determinar si debemos utilizar los modelos balísticos o semi-clásicos de transporte de carga necesitamos conocer la probabilidad de dispersión de electrones en el canal. Esto depende de la longitud del canal y de la calidad del semiconductor.

El número de eventos de dispersión en el canal viene dado por\(\tau /\tau_{m}\) dónde\(\tau\) está el tiempo de tránsito del electrón, y\(\tau_{m}\) es su tiempo de dispersión promedio. Relacionar el tiempo de tránsito con la velocidad portadora, y\(\tau_{m}\) con la definición de movilidad en la Ecuación (4.12.2) da:

\[ \frac{\tau}{\tau_{m}} = \frac{l/v}{m_{eff}\ \mu/q}=\frac{l^{2}/\mu V_{SD}}{m_{eff}\ \mu/q} = \frac{ql^{2}}{m_{eff}V_{SD}\ \mu^{2}} \]

Esta expresión se representa en la Figura 4.14.3 asumiendo un conductor de Si con\(V_{DS} = 1V\),\(\mu = 300 cm^{2}/Vs\) y\(m_{eff} = 0.5 \times m_{0}\), donde\(m_{0}\) está la masa del electrón. Muestra que se espera que el silicio cruce al régimen balístico para longitudes de aproximadamente l < 50nm.

Figura\(\PageIndex{3}\): El número esperado de eventos de dispersión de electrones en Si en función de la longitud del canal. El umbral de operación balística ocurre para longitudes de canal de aproximadamente 50 nm.