4.14: Problemas

1. Considere el dispositivo de metal/nanoalambre/metal que se muestra a continuación. Supongamos que el nanohilo es un conductor unidimensional ideal sin dispersión.

Figura\(\PageIndex{1}\): Un nanohilo termoeléctrico.

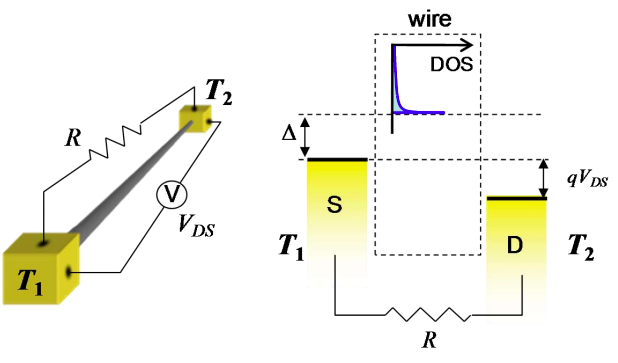
El contacto de la fuente se calienta a temperatura\(T_{1}\), mientras que el contacto de drenaje permanece a temperatura\(T_{2}\). Supongamos que la separación de energía entre la fuente y la parte inferior de la banda de conducción (\(\Delta\)) es independiente del sesgo. Supongamos también eso\(\Delta \ggkT_{1}\).

(a) Ahora los contactos están cortocircuitados juntos, es decir, R → 0. ¿Cuál es la corriente que fluye? (Esta es la 'corriente de cortocircuito').

(b) A continuación supongamos que los contactos son devueltos a circuito abierto, es decir, R → ∞. ¿Cuál es el voltaje entre los contactos? (Este es el 'voltaje de circuito abierto')

2. La relación de dispersión para una partícula relativista viene dada por\(E = \sqrt{p^{2}c^{2}+(m_{0}c^{2})^{2}}\) dónde\(E = \hbar \omega\) y\(p = \hbar k\). Encuentra la velocidad de grupo de esta partícula.

3. La velocidad del grupo viene dada por\(v_{S} = \frac{d}{dt} \left< x\right>\). \(\frac{d}{dt} \left< x\right> = \left< \frac{1}{\hbar}\frac{dE}{dk}\right>\)Demuéstralo.

4. Encuentre la masa efectiva para un electrón en un conductor con la relación de dispersión:

\[ E(k) = 5-2Vcos(ka),\ |k|<\frac{\pi}{a} \nonumber \]

donde V y a son constantes positivas.

5. El grafeno presenta una relación de dispersión similar a fotones. Supongamos que la velocidad del portador es independiente de la energía del portador e igual a la velocidad de la luz, c. Con base en la alta velocidad de los portadores en grafeno, a menudo se argumenta que los transistores de grafeno serán más rápidos que los transistores similares construidos a partir de otros materiales.

(a) Dibujar la relación de dispersión de un alambre de grafeno. Supongamos que el cable tiene solo un modo.

(b) Dado un alambre de longitud, l, construido de grafeno balístico, supongamos que inyectamos un pulso portador como se muestra a continuación. f es la función de distribución, es decir, cuando f = 1 cada estado está completamente lleno. ¿Cuál es el voltaje aplicado?

Figura\(\PageIndex{2}\): La distribución de electrones en el alambre de grafeno.

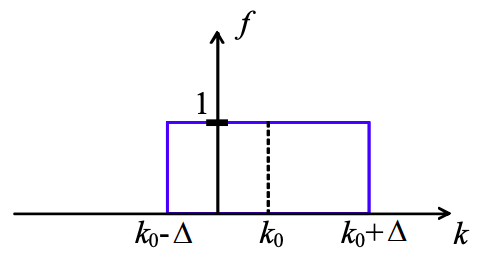
c) ¿Cuántos portadores están contenidos en el pulso?

d) Determinar la corriente transportada por el cable a partir de la velocidad del grupo y el número de portadores.

(e) ¿Cuál es la conductancia del cable?

(f) Ahora supongamos que el grafeno se utiliza para accionar una capacitancia de carga de valor C. ¿Cuál es la constante de tiempo del sistema? ¿Cómo se compara el alambre de grafeno con otros alambres 1d?

6. Este problema se refiere al cable balístico 1-D que se encuentra a continuación. Las X en el alambre son representativas de sitios de dispersión elástica, cada uno con transmisión, T5. Supongamos\(E_{C} < \mu_{S}, \mu_{D}\) dónde

Figura\(\PageIndex{3}\): Nanoalambre balístico con dos sitios de dispersión.

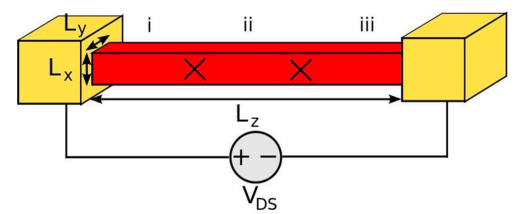
(a) Para T = 1.0, graficar la función de relleno en las posiciones (i), (ii) y (iii) a lo largo del eje z.

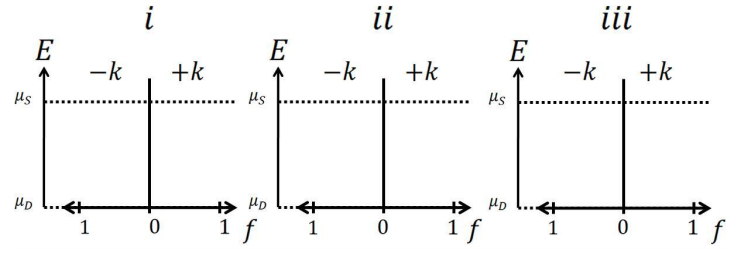
(b) Para T = 0.5, graficar la función de relleno en las posiciones (i), (ii) y (iii) a lo largo del eje z.

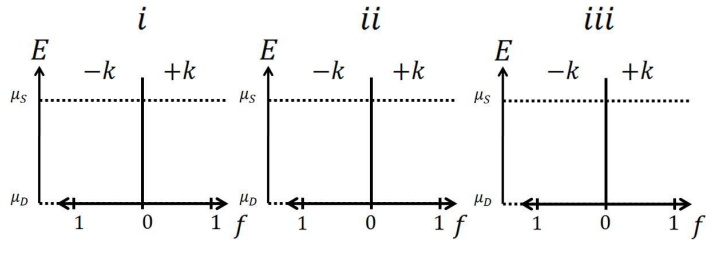
(c) Considerar un número muy grande de sitios de dispersión a lo largo del alambre, cada uno con T = 0.5. Trazar la función de llenado en la fuente (i), en el punto medio del alambre (ii) y en el drenaje (iii).