5.9: Transconductancia

Un transistor de efecto de campo es una fuente de corriente controlada por voltaje. Su entrada es el potencial de puerta, y la salida es la corriente de fuente-drenaje. En aplicaciones, solemos desear que el FET amplifique pequeños cambios en\(V_{GS}\). Así, una importante figura de mérito para un FET es la transconductancia, definida como

\[ g_{m} = \frac{dI_{ds}}{dV_{gs}} \nonumber \]

En el estado OFF, la capacitancia cuántica es pequeña y la única influencia de la puerta en el FET es su control electrostático del potencial del canal. De la Ecuación (5.3.1), vemos que este control se maximiza cuando

\[ C_{G} \gg C_{S},C_{D} \nonumber \]

Este es un objetivo de diseño importante para los FET. Bajo este límite la transconductancia se expresa comúnmente como:

\[ \frac{g_{m}}{I_{ds}} = \frac{1}{I_{ds}}\frac{dI_{ds}}{dV_{gs}} = \frac{q}{kT} \nonumber \]

Se puede lograr un buen control electrostático del canal ya sea aumentando la constante dieléctrica del aislante de puerta, o reduciendo el grosor del aislante de puerta.

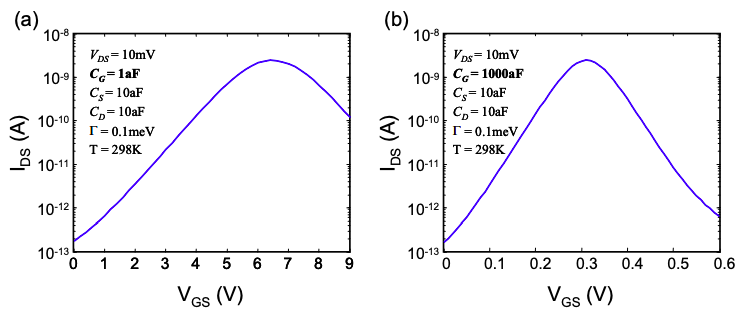
Una buena regla general es que la puerta debe estar mucho más cerca del canal que los contactos de fuente o drenaje. La Figura 5.9.1 muestra el impacto de la variación\(C_{G}\) en nuestro transistor molecular C60. El aumento\(C_{G}\) desplaza el voltaje de la puerta de conmutación mucho más bajo.

Curiosamente, para obtener esta característica ideal,\(C_{G}\) aumentamos en tres órdenes de magnitud en relación con el valor más práctico utilizado originalmente. Esto corresponde a aumentar la constante dieléctrica o reducir la separación puerta-canal en tres órdenes de magnitud.

Figura\(\PageIndex{1}\): Comparación de dos FET C60. En (a) la puerta tiene un control electrostático deficiente sobre el canal como lo demuestra el pequeño\(C_{G}\). En (b) el control es mejor, y el voltaje de conmutación es mucho menor.

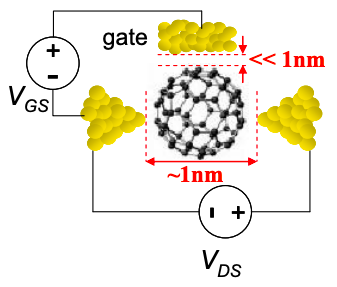
Para un transistor molecular con separación fuente-drenaje de unos pocos nanómetros, el aislador de puerta debe ser solo unos pocos Ångstroms, demasiado delgado para aislar suficientemente la puerta. Esto representa un obstáculo posiblemente insuperable para dispositivos de canal 0-d como FET de molécula única.

Figura\(\PageIndex{2}\): Para una alta transconductancia, la capacitancia de la puerta debe ser mucho mayor que las capacitancias de la fuente o del canal de drenaje. Esto obliga a separaciones de puerta-canal imprácticamente pequeñas en transistores moleculares.

FET 1d y 2d

La ecuación central de la conducción es

\[ I=\frac{q(N_{S}-N_{D})}{\tau} \nonumber \]

En 0-d la constante de tiempo\(\tau\),, se definió como la suma del tiempo de transferencia de electrones interfacial\(\tau_{S}\) y\(\tau_{D}\), que a su vez puede considerarse como representaciones de la energía de interacción entre el conductor 0-d y los contactos fuente y drenaje:\(\tau_{S}=\Gamma_{S}/\hbar\) y\(\tau_{D}=\Gamma_{D}/\hbar\), respectivamente.

Figura\(\PageIndex{3}\): (a) Los tiempos de transferencia de electrones en un conductor 0-d están relacionados con la energía de interacción\(\Gamma\) entre el contacto y el conductor. (b) En dimensiones superiores, debemos determinar el tiempo de tránsito a partir de la velocidad de los electrones.

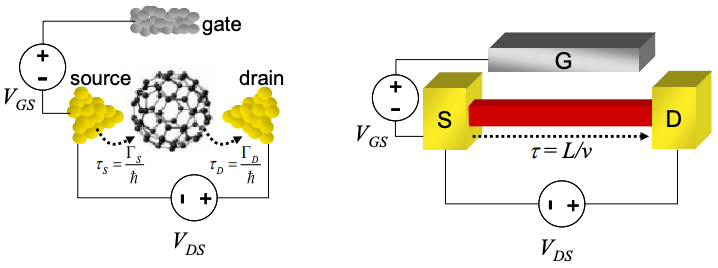
En dimensiones superiores, sin embargo, los tiempos de transferencia de electrones en los contactos son menos importantes. Más bien,\(\tau\) es el tiempo de tránsito para un electrón en el conductor. Está dado por

\[ \tau=\frac{L_{x}}{v_{x}} \nonumber \]

donde\(L_{x}\) es la longitud del canal, y\(v_{x}\) es la componente de velocidad del electrón paralela a la corriente fuente-drenaje. Es importante señalar que en los conductores 1-d, 2-d y 3-d el tiempo de tránsito depende de la energía del electrón ya que la velocidad del electrón,\(v_{x}\), depende de la energía.

El otro cambio importante del modelo 0-d se refiere a la densidad de estados. En 0-d todos los estados son accesibles a los electrones tanto de la fuente como de los contactos de drenaje. Pero en los dispositivos balísticos de dimensiones superiores, los electrones inyectados desde la fuente solo pueden acceder a estados con momentos dirigidos lejos de la fuente. Llamamos a estos +k estados. De manera similar, el drenaje solo inyecta electrones en estados —k. Así, rompemos la relación de dispersión y densidad de estados en dos partes, la densidad de +k estados viene dada por\(g^{+}(E)dE\) y la densidad de —k estados viene dada por\(g^{-}(E)dE\).

Para resumir, en 1-d, 2-d y 3-d las ecuaciones fundamentales para un transistor son:

\[ U_{ES} = -qV_{GS}\frac{C_{G}}{C_{ES}}-qV_{DS}\frac{C_{D}}{C_{ES}}+\frac{q^{2}}{C_{ES}}(N-N_{0}) \nonumber \]

\[ N=N_{S}+N_{D} \nonumber \]

\[ I=\frac{q}{\tau}(N_{S}-N_{D}) \nonumber \]

donde

\[ N_{S} = \int^{\infty}_{-\infty} g^{+}(E-U)f(E, \mu_{S})dE \nonumber \]

\[ N_{D} = \int^{+\infty}_{-\infty} g^{-}(E-U)f(E, \mu_{D})dE \nonumber \]